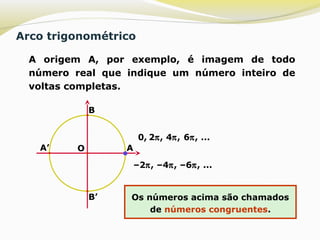
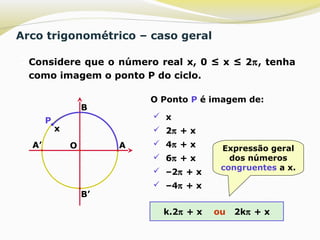
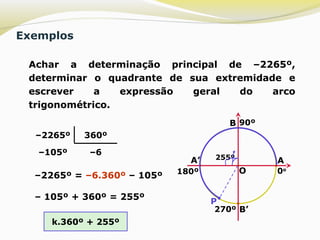
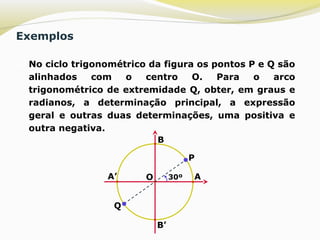
O documento explica o conceito de arco trigonométrico, definindo-o como o conjunto de todos os números reais cuja expressão geral é 2kπ + x, onde x é a determinação principal do arco, ou seja, o número real entre 0 e 2π que tem como imagem o ponto do ciclo trigonométrico que é a extremidade do arco. O texto também mostra como encontrar a determinação principal de um número real dado e escrever a expressão geral correspondente ao arco trigonométrico.

2. Arco trigonométrico
 Até aqui marcamos no ciclo trigonométrico
imagens de números reais do intervalo [–2π, 2π[.
São os números da 1ª volta positiva ou da 1ª volta
negativa.
 A localização da imagem de um número real
permite que sejam dadas, no ciclo, tantas voltas
quantas forem necessárias, tanto no sentido
positivo como no negativo.
Cada ponto do ciclo trigonométrico é
imagem de infinitos números reais.

3. Arco trigonométrico
 A origem A, por exemplo, é imagem de todo
número real que indique um número inteiro de
voltas completas.
O A
B
A’
B’
0, 2π, 4π, 6π, ...
–2π, –4π, –6π, ...
Os números acima são chamados
de números congruentes.

4. Arco trigonométrico – caso geral
 Considere que o número real x, 0 ≤ x ≤ 2π, tenha
como imagem o ponto P do ciclo.
O A
B
A’
B’
P
x
O Ponto P é imagem de:
 x
 2π + x
 4π + x
 6π + x
 –2π + x
 –4π + x
k.2π + x ou 2kπ + x
Expressão geral
dos números
congruentes a x.

5. Arco trigonométrico
 Seja x um número real, 0 ≤ x < 2π, com imagem
num ponto P do ciclo. Chamamos de Arco
trigonométrico de extremidade P o conjunto de
todos os números reais cuja expressão geral é 2kπ
+ x, com k inteiro.
 Cada um dos infinitos números congruentes que
definem um arco trigonométrico é uma
determinação do arco.
 Existe uma única determinação x que está na 1ª
volta positiva. Ela é chamada de determinação
principal.

6. Encontrando a determinação principal
 Conhecendo-se uma das determinações de um
arco trigonométrico, podemos encontrar sua
determinação principal. Com a determinação
principal, podemos raciocinar na primeira volta
positiva, o que facilita a localização da
extremidade do arco.

7. 5110º
360º1910º
Exemplos
 Achar a determinação principal de 1910º e
determinar o quadrante de sua extremidade e
escrever a expressão geral do arco
trigonométrico.
1910º = 5 . 360º + 110º O
A
B
A’
B’
P
110º
90º
0o
180º
270º
k.360º + 110º

8. –6–105º
360º–2265º
Exemplos
 Achar a determinação principal de –2265º,
determinar o quadrante de sua extremidade e
escrever a expressão geral do arco
trigonométrico.
–2265º = –6.360º – 105º
O
A
B
A’
B’
P
255º
90º
0o
180º
270º
– 105º + 360º = 255º
k.360º + 255º

9. Exemplos
 Achar a determinação principal de 49π/5,
determinar o quadrante de sua extremidade e
escrever a expressão geral do arco
trigonométrico.
49π/5 = 9,8 π 8π < 49π/5 < 10π⇒
49π
5
– 8π =
49π – 40π
5
=
9π
5
⇒ 324º, 4º q.
2kπ + 9π/5.

10. Exemplos
 Achar a determinação principal de –17π/3,
determinar o quadrante de sua extremidade e
escrever a expressão geral do arco
trigonométrico.
–17π/3 = –5,6π –6π < –17π/3 < –4π⇒
–17π
3
+ 6π =
–17π + 18π
3
=
π
3
⇒ 60º, 1º q.
2kπ + π/3.

11. Exemplos
 No ciclo trigonométrico da figura os pontos P e Q são
alinhados com o centro O. Para o arco
trigonométrico de extremidade Q, obter, em graus e
radianos, a determinação principal, a expressão
geral e outras duas determinações, uma positiva e
outra negativa.
O A
B
A’
B’
P
Q
30º