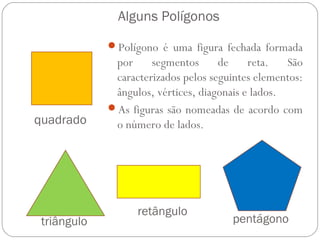
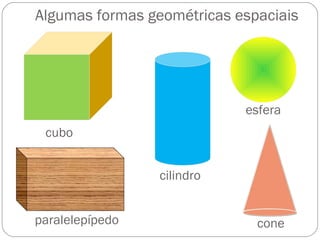
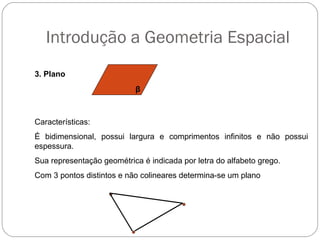
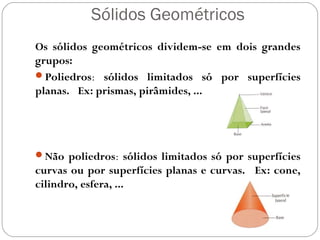
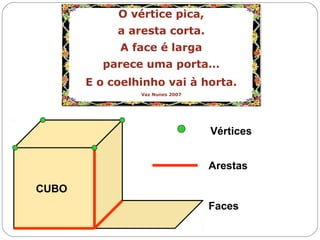
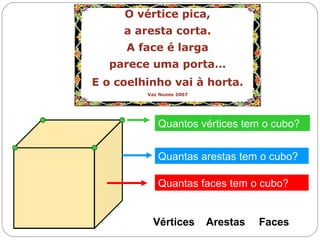
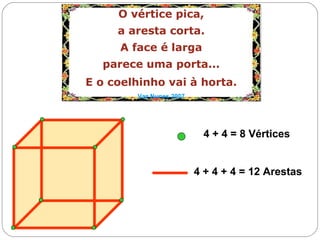
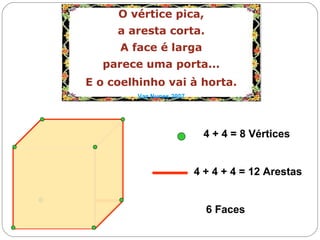
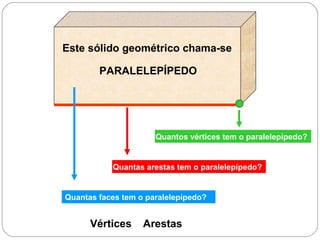
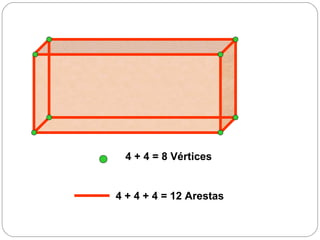
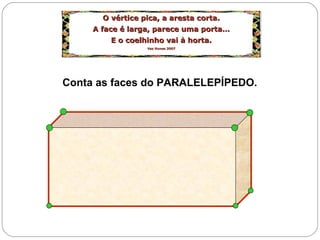
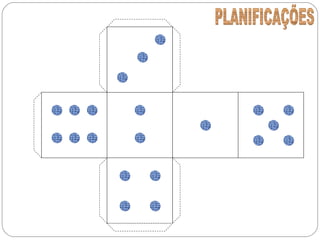
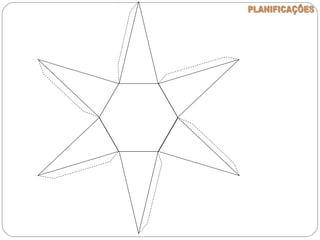
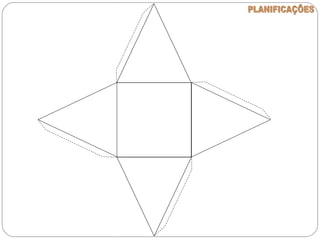
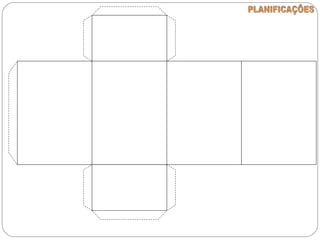
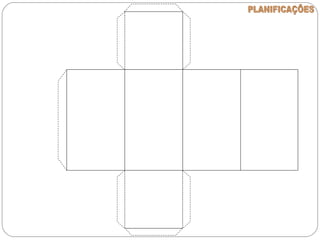
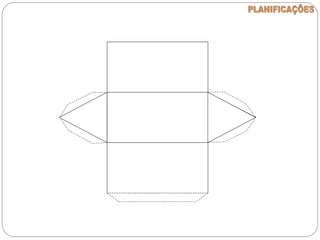
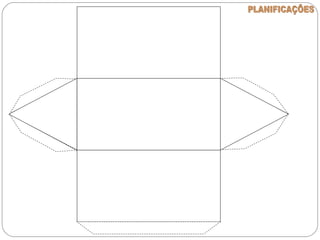
O documento apresenta uma introdução à geometria, definindo-a como o estudo das formas e medidas. Apresenta alguns conceitos básicos como ponto, reta, plano e espaço, além de figuras geométricas planas como polígonos e figuras geométricas espaciais como cubo e paralelepípedo. Explica as características de cada um destes elementos geométricos.

1. Professora: Maria Cristina de A.Tuyama
Colaboradora: Daniela Fontana Almenara
Geometria
Noções Fundamentais
E.E.E.F.M. Cel. Aluízio Pinheiro Ferreira
Rolim de Moura – RO

2. Um pouco de História
Muito antes de criar as linguagens
escritas o homem já tinha atentado para
as formas dos seres e objetos existentes
no mundo.
O homem desenvolveu já nos tempos
pré-históricos centenas de objetos com
as mais variadas formas;
Também retratava em pinturas e
esculturas, as formas de animais
paisagens e objetos com os quais
estavam em contato;

3. Definição
A palavra geometria resulta de duas palavras
gregas: geo, que significa “terra”, e metria,
que significa “medida” .
A Geometria tem por objetivo estudar as
formas (de objetos ou figuras) e estabelecer
relações entre as medidas de suas partes e
entre figuras diferentes.

4. Taj Mahal, na
Índia
No mundo de hoje, as inúmeras obras de engenharia,
arquitetura, artes plásticas, etc mostram a imensa quantidade
de forma que o homem desenvolveu partindo dos
conhecimentos de geometria.
Congresso Nacional,
Brasília

5. Alguns tipos de formas

6. quadrado
Polígono é uma figura fechada formada
por segmentos de reta. São
caracterizados pelos seguintes elementos:
ângulos, vértices, diagonais e lados.
As figuras são nomeadas de acordo com
o número de lados.
triângulo
retângulo
pentágono
Alguns Polígonos

7. Algumas formas geométricas espaciais
cubo
esfera
coneparalelepípedo
cilindro

8. Introdução a Geometria Espacial
1. Ponto P
Características:
Não possui dimensão
Sua representação geométrica é indicada por letra maiúscula
Por um ponto passam infinitas retas

9. Introdução a Geometria Espacial
2. Reta
r
Características:
É unidimensional e tem comprimento infinito
Sua representação geométrica é indicada por letra minúscula
Em uma reta há infinitos pontos

10. Introdução a Geometria Espacial
3. Plano
β
Características:
É bidimensional, possui largura e comprimentos infinitos e não possui
espessura.
Sua representação geométrica é indicada por letra do alfabeto grego.
Com 3 pontos distintos e não colineares determina-se um plano

11. Introdução a Geometria Espacial
4. Espaço: é o conjunto de todos os pontos, retas e planos. É tridimensional.

12. Sólidos Geométricos
Os sólidos geométricos dividem-se em dois grandes
grupos:
Poliedros: sólidos limitados só por superfícies
planas. Ex: prismas, pirâmides, ...
Não poliedros: sólidos limitados só por superfícies
curvas ou por superfícies planas e curvas. Ex: cone,
cilindro, esfera, ...

13. O vértice pica,
a aresta corta.
A face é larga
parece uma porta…
E o coelhinho vai à horta.
Vaz Nunes 2007
O vértice pica,
a aresta corta.
A face é larga
parece uma porta…
E o coelhinho vai à horta.
Vaz Nunes 2007
Vértices
Arestas
Faces
CUBO

14. O vértice pica,
a aresta corta.
A face é larga
parece uma porta…
E o coelhinho vai à horta.
Vaz Nunes 2007
O vértice pica,
a aresta corta.
A face é larga
parece uma porta…
E o coelhinho vai à horta.
Vaz Nunes 2007
Vértices Arestas Faces
Quantos vértices tem o cubo?
Quantas arestas tem o cubo?
Quantas faces tem o cubo?

15. O vértice pica,
a aresta corta.
A face é larga
parece uma porta...
E o coelhinho vai à horta.
Vaz Nunes 2007
O vértice pica,
a aresta corta.
A face é larga
parece uma porta...
E o coelhinho vai à horta.
Vaz Nunes 2007
4 + 4 = 8 Vértices
4 + 4 + 4 = 12 Arestas

16. 4 + 4 = 8 Vértices
6 Faces
4 + 4 + 4 = 12 Arestas
O vértice pica,
a aresta corta.
A face é larga
parece uma porta...
E o coelhinho vai à horta.
Vaz Nunes 2007
O vértice pica,
a aresta corta.
A face é larga
parece uma porta...
E o coelhinho vai à horta.
Vaz Nunes 2007

17. Vértices Arestas
Quantos vértices tem o paralelepípedo?
Quantas arestas tem o paralelepípedo?
Quantas faces tem o paralelepípedo?
Este sólido geométrico chama-se
PARALELEPÍPEDO

18. 4 + 4 = 8 Vértices
4 + 4 + 4 = 12 Arestas

19. O vértice pica, a aresta corta.O vértice pica, a aresta corta.
A face é larga, parece uma porta…A face é larga, parece uma porta…
E o coelhinho vai à horta.E o coelhinho vai à horta.
Vaz Nunes 2007Vaz Nunes 2007
O vértice pica, a aresta corta.O vértice pica, a aresta corta.
A face é larga, parece uma porta…A face é larga, parece uma porta…
E o coelhinho vai à horta.E o coelhinho vai à horta.
Vaz Nunes 2007Vaz Nunes 2007
Conta as faces do PARALELEPÍPEDO.