O documento descreve os passos para determinar a intersecção de um cubo com diferentes planos, resultando em figuras geométricas como triângulos, quadrados e retângulos. Inclui exemplos de planos perpendiculares a diagonais, faces e definidos por três pontos do cubo.

1. • Intersecção de cubos

2. Plano passando por três pontos dados (triângulo)Plano passando por três pontos dados (triângulo)
Plano passando por três pontos dados (trapézio)Plano passando por três pontos dados (trapézio)
Plano passando por três pontos dados (pentágono)Plano passando por três pontos dados (pentágono)
Plano passando por três pontos dados (hexágono)Plano passando por três pontos dados (hexágono)
Plano perpendicular à diagonal espacialPlano perpendicular à diagonal espacial
Plano perpendicular a uma das faces (rectângulo)Plano perpendicular a uma das faces (rectângulo)
Cubos

3. Intersecção de cubos por planos
Planos perpendiculares a uma diagonal espacial
A B
CD
E
F
GH

4. A B
CD
E F
GH
M2
M1
M3
Desta intersecção
resulta um triângulo
equilátero
Exemplo 1
Plano perpendicular a uma diagonal espacial
1º - Traçar o segmento de1º - Traçar o segmento de
recta Mrecta M11MM33..
2º - Traçar o segmento de2º - Traçar o segmento de
recta Mrecta M33MM22..
5º - Desenhar a secção M5º - Desenhar a secção M22MM11MM33
3º - Traçar o segmento de3º - Traçar o segmento de
recta Mrecta M22MM11..

5. A B
CD
E F
GH
Exemplo 2
Plano perpendicular a uma diagonal espacial
Desta intersecção resulta
um triângulo equilátero

6. A B
CD
E F
GH
Exemplo 3
Plano perpendicular a uma diagonal espacial
Desta intersecção resulta
um triângulo equilátero

7. X
Y
z
1º - Traçar a recta XY.1º - Traçar a recta XY.
2º - Traçar a recta paralela a XY, passando em Z.2º - Traçar a recta paralela a XY, passando em Z.
4º - Prolongar a aresta CG.4º - Prolongar a aresta CG.
5º - Determinar o ponto5º - Determinar o ponto II dede
intersecção de XY com CGintersecção de XY com CG
I
6º - Unir o ponto6º - Unir o ponto II com o pontocom o ponto J,J,
determinando o pontodeterminando o ponto KK
3º - Determinar o ponto3º - Determinar o ponto JJ , da aresta BF, da aresta BF
J
7º - Unir os pontos7º - Unir os pontos KK ee YY
KK
8º - Traçar uma recta paralela a8º - Traçar uma recta paralela a K YK Y,,
passando empassando em ZZ definindo o pontodefinindo o ponto LL
9º - Unir os pontos9º - Unir os pontos LL ee XX
L
10º -Está determinada a secção10º -Está determinada a secção
[XY[XYKJKJZZLL]]
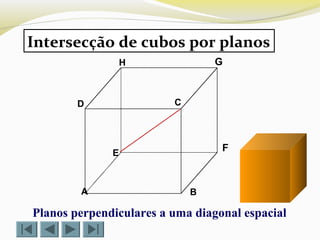
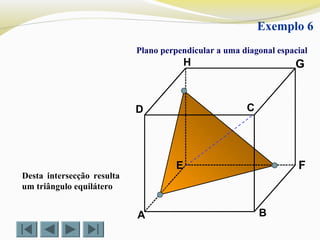
Plano perpendicular a uma diagonal espacial
Passando pelo centro
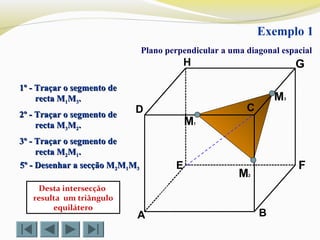
Exemplo 4
Desta intersecção resulta um hexagono regular

8. X
Y
z
1º - Traçar a recta XY.1º - Traçar a recta XY.
2º - Traçar a recta paralela a XY, passando em Z.2º - Traçar a recta paralela a XY, passando em Z.
4º - Prolongar a aresta CG.4º - Prolongar a aresta CG.
5º - Determinar o ponto5º - Determinar o ponto II dede
intersecção de XY com CGintersecção de XY com CG
I
6º - Unir o ponto6º - Unir o ponto II com o pontocom o ponto J,J,
determinando o pontodeterminando o ponto KK
3º - Determinar o ponto3º - Determinar o ponto JJ , da aresta BF, da aresta BF
J
7º - Unir os pontos7º - Unir os pontos KK ee YY
KK
8º - Traçar uma recta paralela a8º - Traçar uma recta paralela a K YK Y,,
passando empassando em ZZ definindo o pontodefinindo o ponto LL
9º - Unir os pontos9º - Unir os pontos LL ee XX
L
10º -Está determinada a secção10º -Está determinada a secção
[XY[XYKJKJZZLL]]
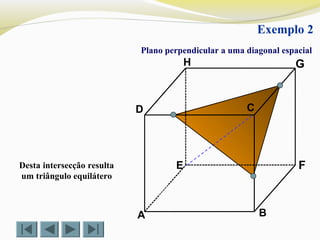
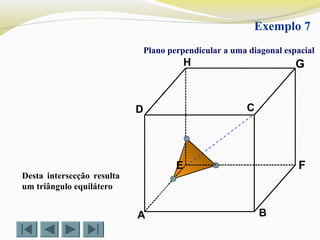
Plano perpendicular a uma diagonal espacial
Exemplo 5
Desta intersecção resulta um hexágono

9. A B
CD
E F
GH
Exemplo 6
Plano perpendicular a uma diagonal espacial
Desta intersecção resulta
um triângulo equilátero

10. A B
CD
E F
GH
Exemplo 7
Plano perpendicular a uma diagonal espacial
Desta intersecção resulta
um triângulo equilátero

11. Intersecção de cubos por planos
perpendiculares a uma face

12. A B
CD
E F
GH
Intersecção do cubo com um plano perpendicular a uma face (ou base)Intersecção do cubo com um plano perpendicular a uma face (ou base)
(RETÂNGULO)(RETÂNGULO)
Exemplo 1Exemplo 1

13. A B
CD
E F
GH
Intersecção do cubo com um plano perpendicular a uma face (ou base)Intersecção do cubo com um plano perpendicular a uma face (ou base)
(RETÂNGULO)(RETÂNGULO)
Exemplo 2Exemplo 2

14. A B
CD
E F
GH
Intersecção do cubo com um plano perpendicular a uma face (ou base)Intersecção do cubo com um plano perpendicular a uma face (ou base)
(RETÂNGULO)(RETÂNGULO)
Exemplo 3Exemplo 3

15. A B
CD
E F
GH
Intersecção do cubo com um plano perpendicular a uma face (ou base)Intersecção do cubo com um plano perpendicular a uma face (ou base)
(RETÂNGULO)(RETÂNGULO)
Exemplo 4Exemplo 4

16. A B
CD
E F
GH
Exemplo 5Exemplo 5
Intersecção do cubo com um plano perpendicular a uma face (ou base)Intersecção do cubo com um plano perpendicular a uma face (ou base)
(RETÂNGULO)(RETÂNGULO)

17. A B
CD
E F
GH
Exemplo 6Exemplo 6
Intersecção do cubo com um plano perpendicular a uma face (ou base)Intersecção do cubo com um plano perpendicular a uma face (ou base)
(RETÂNGULO)(RETÂNGULO)

18. A B
CD
E F
GH
Exemplo 7Exemplo 7
Intersecção do cubo com um plano perpendicular a uma face (ou base)Intersecção do cubo com um plano perpendicular a uma face (ou base)
(RETÂNGULO)(RETÂNGULO)

19. A B
CD
E F
GH
Exemplo 8Exemplo 8
Intersecção do cubo com um plano perpendicular a uma face (ou base)Intersecção do cubo com um plano perpendicular a uma face (ou base)
(RETÂNGULO)(RETÂNGULO)

20. A B
CD
E F
GH
Exemplo 9Exemplo 9
Intersecção do cubo com um plano perpendicular a uma face (ou base)Intersecção do cubo com um plano perpendicular a uma face (ou base)
(RETÂNGULO)(RETÂNGULO)

21. A B
CD
E F
GH
Exemplo 10Exemplo 10
Intersecção do cubo com um plano perpendicular a uma face (ou base)Intersecção do cubo com um plano perpendicular a uma face (ou base)
(RETÂNGULO)(RETÂNGULO)

22. A B
CD
E F
GH
Exemplo 11Exemplo 11
Intersecção do cubo com um plano perpendicular a uma face (ou base)Intersecção do cubo com um plano perpendicular a uma face (ou base)
(RETÂNGULO)(RETÂNGULO)

23. A B
CD
E F
GH
Exemplo 12Exemplo 12
Intersecção do cubo com um plano perpendicular a uma face (ou base)Intersecção do cubo com um plano perpendicular a uma face (ou base)
(RETÂNGULO)(RETÂNGULO)

24. A B
CD
E F
GH
Exemplo 13Exemplo 13
Intersecção do cubo com um plano perpendicular a uma face (ou base)Intersecção do cubo com um plano perpendicular a uma face (ou base)
(RETÂNGULO)(RETÂNGULO)

25. A B
CD
E F
GH
Intersecção do cubo com um plano perpendicular á base e paralelo aIntersecção do cubo com um plano perpendicular á base e paralelo a
uma facea uma faceuma facea uma face (QUADRADO)(QUADRADO)
Exemplo 14Exemplo 14

26. Intersecção de cubos por planos
definidos por três pontos

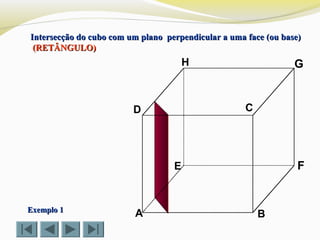
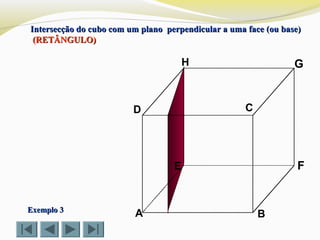
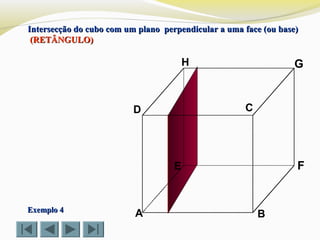
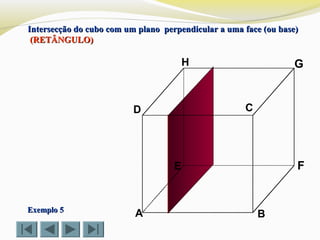
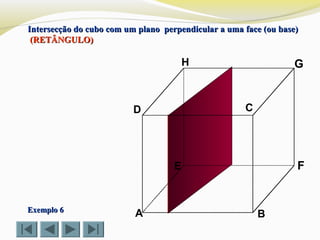
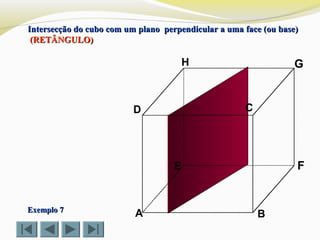
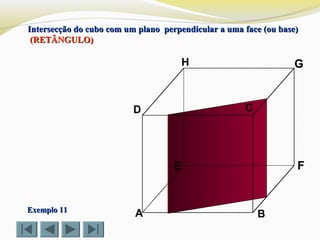
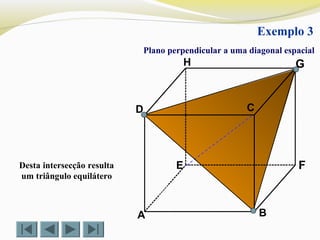
27. Determinar a intersecção do cubo com um plano definido por doisDeterminar a intersecção do cubo com um plano definido por dois
vértices (D e G) e o ponto Xvértices (D e G) e o ponto X (TRIÂNGULO)(TRIÂNGULO)
X
1º - Traçar o segmento [DG].1º - Traçar o segmento [DG].
2º -Traçar o segmento [GX]2º -Traçar o segmento [GX]
3º -Traçar o segmento [XD]3º -Traçar o segmento [XD]
4º - Desenhar a secção DGX4º - Desenhar a secção DGX
Exemplo 1Exemplo 1

28. X
1º - Traçar o segmento [DG].1º - Traçar o segmento [DG].
2º -Traçar o segmento [GX]2º -Traçar o segmento [GX]
3º -Traçar o segmento [XD]3º -Traçar o segmento [XD]
4º - Desenhar a secção DGX4º - Desenhar a secção DGX
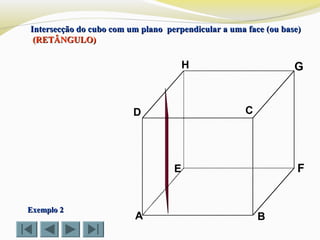
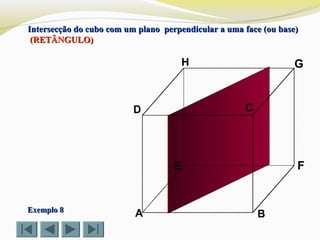
Exemplo 2Exemplo 2
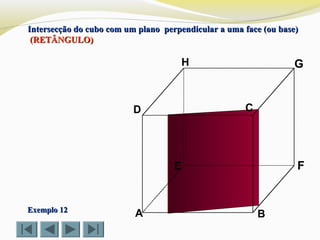
Determinar a intersecção do cubo com um plano definido por doisDeterminar a intersecção do cubo com um plano definido por dois
vértices (D e G) e o ponto Xvértices (D e G) e o ponto X (TRIÂNGULO)(TRIÂNGULO)

29. 1º - Traçar o segmento [DG].1º - Traçar o segmento [DG].
2º -Traçar o segmento [GX]2º -Traçar o segmento [GX]
3º -Traçar o segmento [XD]3º -Traçar o segmento [XD]
4º - Desenhar a secção DGX4º - Desenhar a secção DGX
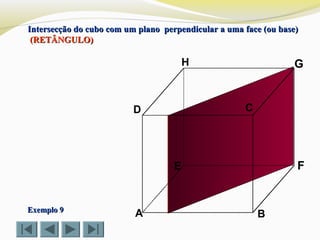
Exemplo 3Exemplo 3
X
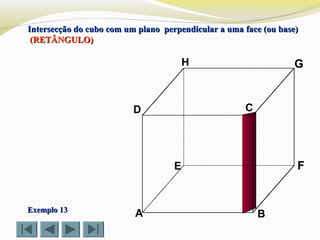
Determinar a intersecção do cubo com um plano definido por doisDeterminar a intersecção do cubo com um plano definido por dois
vértices (D e G) e o ponto Xvértices (D e G) e o ponto X (TRIÂNGULO)(TRIÂNGULO)

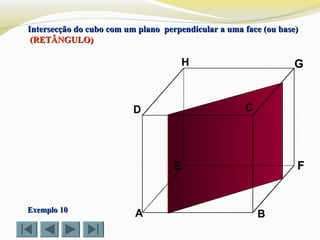
30. Determinar a intersecção do cubo com um plano definido por trêsDeterminar a intersecção do cubo com um plano definido por três
vértices (D, G e B )vértices (D, G e B ) (TRIÂNGULO)(TRIÂNGULO)
1º - Traçar o segmento [DG].1º - Traçar o segmento [DG].
2º -Traçar o segmento [GB]2º -Traçar o segmento [GB]
3º -Traçar o segmento [BD]3º -Traçar o segmento [BD]
4º - Desenhar a secção DGB4º - Desenhar a secção DGB
Exemplo 4Exemplo 4

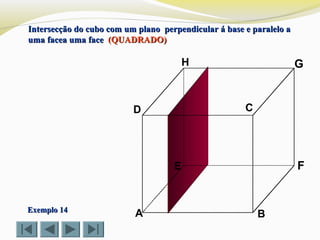
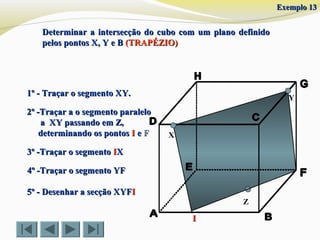
31. Determinar a intersecção do cubo com um plano definido pelosDeterminar a intersecção do cubo com um plano definido pelos
pontos X, Y e Bpontos X, Y e B (TRAPÉZIO)(TRAPÉZIO)
X
Y1º - Traçar o segmento [XY].1º - Traçar o segmento [XY].
2º -Traçar o segmento paralelo2º -Traçar o segmento paralelo
a [XY] passando em Z,a [XY] passando em Z,
determinando os pontosdeterminando os pontos II ee JJ
3º -Traçar o segmento [X3º -Traçar o segmento [XII]]
5º - Desenhar a secção XY5º - Desenhar a secção XYIJIJ
Z JJ
II
4º -Traçar o segmento [Y4º -Traçar o segmento [YJJ]]
Exemplo 12Exemplo 12

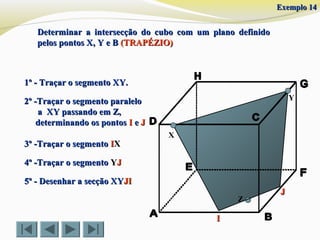
32. Determinar a intersecção do cubo com um plano definido por doisDeterminar a intersecção do cubo com um plano definido por dois
vértices (D e G ) e o ponto Xvértices (D e G ) e o ponto X (QUADRILÁTERO)(QUADRILÁTERO)
X
1º - Traçar o segmento [DG].1º - Traçar o segmento [DG].
2º -Traçar o segmento [GX]2º -Traçar o segmento [GX]
4º -Traçar o segmento [4º -Traçar o segmento [IID]D]
5º - Desenhar a secção DGX5º - Desenhar a secção DGXII
3º -Traçar o segmento paralela3º -Traçar o segmento paralela
a [DG], passando em X,a [DG], passando em X,
determinando o pontodeterminando o ponto II
I
Exemplo 5Exemplo 5

33. Determinar a intersecção do cubo com um plano definido porDeterminar a intersecção do cubo com um plano definido por
três vértices (D, G e F)três vértices (D, G e F) (RECTÂNGULO)(RECTÂNGULO)
1º - Traçar o segmento [DG].1º - Traçar o segmento [DG].
2º -Traçar o segmento [GF]2º -Traçar o segmento [GF]
4º -Traçar a aresta [AD]4º -Traçar a aresta [AD]
5º - Desenhar a secção DGFA5º - Desenhar a secção DGFA
3º -Traçar o segmento paralelo3º -Traçar o segmento paralelo
a[DG], passando em Fa[DG], passando em F
Exemplo 6Exemplo 6

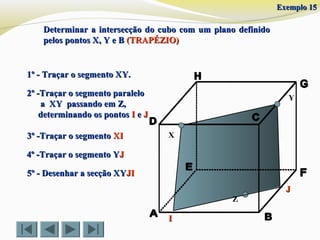
34. Determinar a intersecção do cubo com um plano definido porDeterminar a intersecção do cubo com um plano definido por
dois vértices (D e G ) e o ponto Xdois vértices (D e G ) e o ponto X (TRAPÉZIO)(TRAPÉZIO)
X
1º - Traçar o segmento [DG].1º - Traçar o segmento [DG].
3º -Traçar o segmento [DX]3º -Traçar o segmento [DX]
4º -Traçar o segmento [4º -Traçar o segmento [IIG]G]
5º - Desenhar a secção DG5º - Desenhar a secção DGIIXX
2º -Traçar o segmento paralelo2º -Traçar o segmento paralelo
a [DG], passando em X,a [DG], passando em X,
determinando o pontodeterminando o ponto II
I
Exemplo 7Exemplo 7

35. Determinar a intersecção do cubo com um plano definidoDeterminar a intersecção do cubo com um plano definido
pelos pontos X, Y e Bpelos pontos X, Y e B (TRAPÉZIO)(TRAPÉZIO)
X
Y
1º - Traçar o segmento XY.1º - Traçar o segmento XY.
2º -Traçar a o segmento paralelo2º -Traçar a o segmento paralelo
a XY passando em Z,a XY passando em Z,
determinando os pontosdeterminando os pontos II ee FF
3º -Traçar o segmento3º -Traçar o segmento IIXX
5º - Desenhar a secção XYF5º - Desenhar a secção XYFII
Z
II
4º -Traçar o segmento YF4º -Traçar o segmento YF
Exemplo 13Exemplo 13

36. Determinar a intersecção do cubo com um plano definidoDeterminar a intersecção do cubo com um plano definido
pelos pontos X, Y e Bpelos pontos X, Y e B (TRAPÉZIO)(TRAPÉZIO)
X
Y
1º - Traçar o segmento XY.1º - Traçar o segmento XY.
2º -Traçar o segmento paralelo2º -Traçar o segmento paralelo
a XY passando em Z,a XY passando em Z,
determinando os pontosdeterminando os pontos II ee JJ
4º -Traçar o segmento4º -Traçar o segmento YYJJ
5º - Desenhar a secção XY5º - Desenhar a secção XYJIJI
Z
II
JJ
3º -Traçar o segmento3º -Traçar o segmento IIXX
Exemplo 14Exemplo 14

37. Determinar a intersecção do cubo com um plano definidoDeterminar a intersecção do cubo com um plano definido
pelos pontos X, Y e Bpelos pontos X, Y e B (TRAPÉZIO)(TRAPÉZIO)
X
Y
1º - Traçar o segmento XY.1º - Traçar o segmento XY.
2º -Traçar o segmento paralelo2º -Traçar o segmento paralelo
a XY passando em Z,a XY passando em Z,
determinando os pontosdeterminando os pontos II ee JJ
3º -Traçar o segmento3º -Traçar o segmento XIXI
5º - Desenhar a secção XY5º - Desenhar a secção XYJIJI
Z
II
4º -Traçar o segmento Y4º -Traçar o segmento YJJ
JJ
Exemplo 15Exemplo 15

38. X
Y
Z
1º - Traçar a recta XZ.1º - Traçar a recta XZ.
2º - Traçar a recta YZ.2º - Traçar a recta YZ.
4º - Traçar uma paralela a YZ,4º - Traçar uma paralela a YZ,
passando porpassando por JJ e encontrare encontrar KK
5º - Unir o ponto5º - Unir o ponto KK com o pontocom o ponto X,X,
3º - Traçar uma paralela a XZ,3º - Traçar uma paralela a XZ,
passando por Y e encontrarpassando por Y e encontrar JJ
J
6º - Está determinada a secção6º - Está determinada a secção
[XY[XYJJZZKK]]
K
Determinar a intersecção do cubo com o plano XYZDeterminar a intersecção do cubo com o plano XYZ
((PENTÁGONOPENTÁGONO))
Exemplo 16Exemplo 16

39. X
Y
z
1º - Traçar a recta XY.1º - Traçar a recta XY.
2º - Prolongar a aresta CG.2º - Prolongar a aresta CG.
4º - Unir o ponto4º - Unir o ponto ZZ com o pontocom o ponto I,I,
determinando o pontodeterminando o ponto JJ na aresta GFna aresta GF
5º - Unir o ponto5º - Unir o ponto JJ com o pontocom o ponto Y,Y,
I
6º - Traçar uma recta paralela a6º - Traçar uma recta paralela a J YJ Y,,
passando empassando em ZZ definindo o pontodefinindo o ponto KK
na arestana aresta ADAD
3º - Determinar o ponto3º - Determinar o ponto II dede
intersecção de XY com CGintersecção de XY com CG
J
7º - Unir os pontos7º - Unir os pontos KK ee XX
8º - Está determinada a secção8º - Está determinada a secção
[XYJZK][XYJZK]
K
Exemplo 17Exemplo 17
Determinar a intersecção do cubo com o plano XYZDeterminar a intersecção do cubo com o plano XYZ
((PENTÁGONOPENTÁGONO))

40. Determinar a intersecção do cubo com o plano XYZDeterminar a intersecção do cubo com o plano XYZ
((HEXÁGONOHEXÁGONO))
X
Y
z
1º - Traçar a recta XY.1º - Traçar a recta XY.
2º - Traçar a recta paralela a XY, passando em Z.2º - Traçar a recta paralela a XY, passando em Z.
4º - Prolongar a aresta CG.4º - Prolongar a aresta CG.
5º - Determinar o ponto5º - Determinar o ponto II dede
intersecção de XY com CGintersecção de XY com CG
I
6º - Unir o ponto6º - Unir o ponto II com o pontocom o ponto J,J,
determinando o pontodeterminando o ponto KK
3º - Determinar o ponto3º - Determinar o ponto JJ , da aresta BF, da aresta BF
J
7º - Unir os pontos7º - Unir os pontos KK ee YY
KK
8º - Traçar uma recta paralela a8º - Traçar uma recta paralela a K YK Y,,
passando empassando em ZZ definindo o pontodefinindo o ponto LL
9º - Unir os pontos9º - Unir os pontos LL ee XX L
10º -Está determinada a secção10º -Está determinada a secção
[XY[XYKJKJZZLL]]
Exemplo 18Exemplo 18