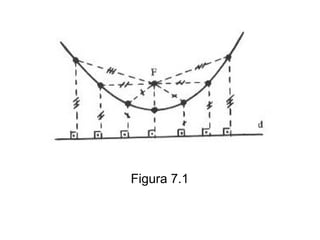
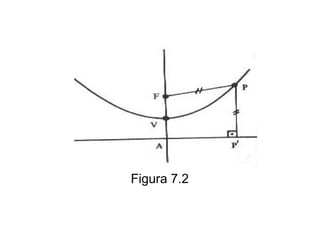
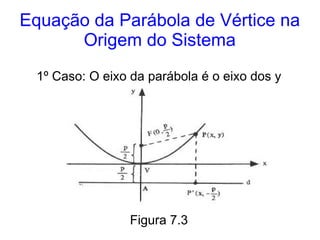
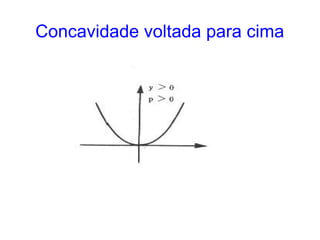
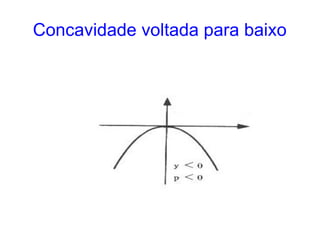
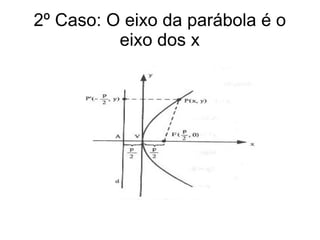
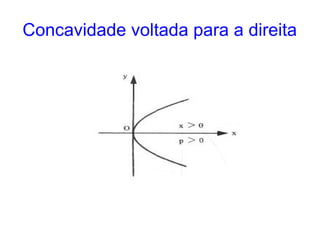
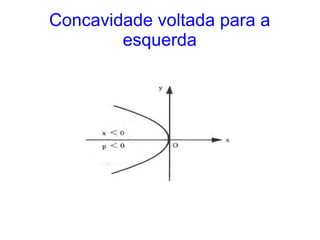
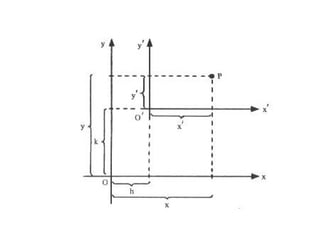
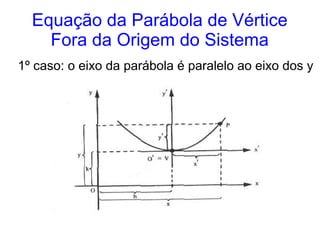
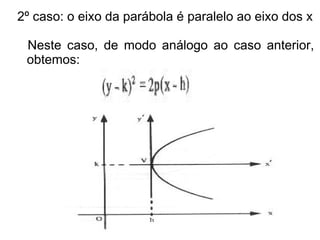
Este documento resume as propriedades básicas das cônicas, especificamente parábolas. Explica que uma parábola é o lugar geométrico dos pontos equidistantes de um ponto focal e uma reta diretriz. Detalha os elementos da parábola, como foco, diretriz e vértice, e apresenta as equações canônicas da parábola para diferentes orientações do eixo.

1. Universidade Federal do
Triângulo Mineiro – UFTM
Cônicas
Prof.: Daniel Oliveira Veronese

2. O que é uma
Superfície Cônica?
Uma superfície cônica de revolução é a superfície
gerada pela rotação completa de uma reta (geratriz) em
torno de outra reta (eixo), formando com esta sempre o
mesmo ângulo, até completar uma revolução (volta
completa). Ao ponto comum à geratriz e ao eixo
chama-se vértice.

4. O que é uma Cônica?
É chamada de Cônica toda curva
que se obtém como interseção de
um plano com uma superfície cônica.

5. Obs.: Quando o plano que intersecta a
superfície cônica passa pelo vértice, a
seção obtida é uma cônica degenerada.
Caso contrário, obtemos cônicas não
degeneradas.

6. Cônicas Não Degeneradas
ELIPSE: neste caso, o plano secante não passa pelo
vértice e intersecta todas as posições da geratriz e o eixo.
Além disso, é oblíquo em relação ao eixo.

7. Se, em particular, o plano é perpendicular ao eixo, a
elipse obtida é uma circunferência.

8. Hipérbole: neste caso, o plano secante não passa
pelo vértice e é paralelo ao eixo;

9. Parábola: neste caso, o plano secante não passa pelo
vértice e é paralelo apenas a uma posição da geratriz.

10. Cônicas Degeneradas
Ponto(Elipse degenerada)

11. Duas retas concorrentes(hipérbole degenerada): neste
caso, o plano secante é paralelo ao eixo e passa pelo
vértice.

12. Reta(parábola degenerada): neste caso, o plano secante é
paralelo apenas a uma posição da geratriz e passa pelo
vértice.

13. Enfatizaremos o estudo das cônicas não
degeneradas, ou seja, elipse, hipérbole e
parábola.

14. Parábola
Consideremos em um plano uma reta d e um
ponto F não pertencente a d.
Definimos parábola como sendo o lugar
geométrico dos pontos que são equidistantes
de F e d.

15. Figura 7.1

16. Figura 7.2

17. Observando a figura 7.2 vemos que uma
condição necessária e suficiente para que o
ponto P pertença à parabola é:
d(P,F)=d(P,P').

18. Elementos da Parábola
Foco: ponto F
Diretriz: reta d
Eixo: reta que passa pelo foco sendo
perpendicular à diretriz.
Vértice: é o ponto V de interseção da parábola
com seu eixo.

19. Equação da Parábola de Vértice na
Origem do Sistema
1º Caso: O eixo da parábola é o eixo dos y
Figura 7.3

20. Da definição de parábola obtemos:
ou seja:

21. Sendo assim, obtemos:
ou, simplesmente:
que é equação reduzida da parábola neste caso.

22. Concavidade voltada para cima
dasf

23. Concavidade voltada para baixo

24. 2º Caso: O eixo da parábola é o
eixo dos x

25. Nesse caso, de modo análogo o que foi feito no
primeiro caso, concluímos que:

26. Concavidade voltada para a direita

27. Concavidade voltada para a
esquerda

28. Observação
O número p(que é diferente de zero) é
chamado parâmetro da parábola.

29. Translação de Eixos
Consideremos no plano xOy um ponto O'(h,k),
arbitrário. Vamos introduzir um novo sistema
x'O'y' tal que os eixos O'x' e O'y' tenham a
mesma unidade de medida, a mesma direção e
o mesmo sentido dos eixos Ox e Oy. Nestas
condições, um sistema pode ser obtido do
outro, por meio de uma translação de eixos.

31. Pela figura anterior vemos que:
ou:
que são as fórmulas de translação e que
permitem transformar coordenadas de um
sistema para outro.

32. Equação da Parábola de Vértice
Fora da Origem do Sistema
1º caso: o eixo da parábola é paralelo ao eixo dos y

33. Do que já vimos, sabemos que:
mas:
e daí:
que é a forma padrão da equação de uma
parábola de vértice V(h,k) e eixo paralelo ao
dos y.

34. 2º caso: o eixo da parábola é paralelo ao eixo dos x
Neste caso, de modo análogo ao caso anterior,
obtemos:

35. Equação da Parábola na Forma
Explícita

1º caso: eixo da parábola paralelo ao eixo dos
y

2º caso: eixo da parábola paralelo ao eixo dos
x

36. Exemplos
Serão feitos no caderno!!!!!!