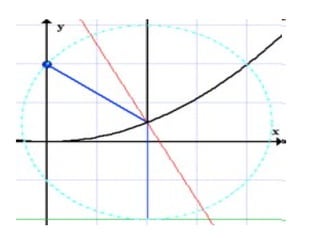
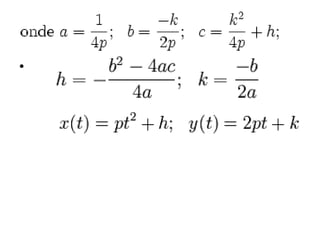Uma parábola é uma curva plana gerada por todos os pontos equidistantes de um ponto fixo chamado de foco e uma reta chamada de diretriz. Ela pode ser definida geometricamente como a interseção de um cone com um plano paralelo à sua geratriz ou analiticamente pela equação geral Ax2 + Bxy + Cy2 + Dx + Ey + F = 0. As parábolas são amplamente utilizadas em antenas parabólicas, radares e faróis de veículos.

1. Parábola

2. A parábola é uma seção cônica gerada pela interseção de uma superfície cônica de segundo grau e um plano paralelo a uma linha geradora do cone (chamada de geratriz). Uma parábola também pode ser definida como o conjunto dos pontos que são equidistantes de um ponto dado (chamado de foco) e de uma reta dada (chamada de diretriz). É uma curva plana . Um caso particular surge quando o plano é tangente à supérfície cônica. Neste caso a interseção é uma parábola degenerada, consistindo de uma reta.

3. Definições e visão geral Equações da geometria analítica Em coordenadas cartesianas , uma parábola com um eixo paralelo ao eixo y com vértice ( h , k ), foco ( h , k + p ), e diretriz y = k - p , com p sendo a distância entre o vértice e o foco, possui a equação ou, alternativamente De maneira geral, uma parábola é uma curva no plano cartesiano definida por uma equação irredutível da forma : Ax 2 + Bxy + Cy 2 + Dx + Ey + F = 0 tal que B 2 = 4 AC , em que todos os coeficientes são reais, em que A e/ou C é não nulo, e na qual mais de uma solução, definindo um par de pontos (x, y) na parábola, existe. O fato da equação ser irredutível significa que ela não pode ser fatorada como um produto de dois fatores lineares.

5. Outras definições geométricas Uma parábola também pode ser caracterizada com uma seção cônica com uma excentricidade igual a 1. Como uma consequência disso, todas as parábolas são similares . Uma parábola também pode ser obtida como o limite de uma sequência de elipses onde um foco é mantido fixo e o outro pode se mover para uma distância cada vez maior do foco em uma direção. Desta forma, uma parábola pode ser considerada a seção do segmento de uma elipse que possui um foco no infinito . A parábola é a transformada inversa de um cardióide . Uma parábola possui um eixo único de simetria reflexiva, o qual passa através de seu foco e é perpendicular à diretriz. O ponto de interseção deste eixo com a parábola é chamado de vértice. Se girarmos uma parábola através de seu eixo em um gráfico de três dimensões temos uma forma conhecida como o parabolóide de revolução. Parábola é uma curva gerada por todos pontos que se situam igualmente distantes de um ponto e uma reta ( chamados de Foco e Diretriz respectivamente ).

7. Equações Cartesiana Eixo vertical de simetria Estas deduções se baseiam em uma parábola de eixo vertical, com vértice ( h , k ) e a distância p entre o vértice e o foco. Por convenção, se o vértice estiver abaixo do foco (equivalentemente, abaixo da diretriz) p é positivo , caso contrário p é negativo . Como um ponto ( x , y ) na parábola dista do foco (de coordenadas ( h , k + p )) tanto quanto da diretriz (linha horizontal de equação cartesiana y = k - p ), podemos escrever:

8. Portanto:

9. O que pode ser reescrito na forma usual ( trinômio do segundo grau ): .

10. Uma equação paramétrica (outras parametrizações são possíveis; a escolha de x(t) foi arbitrária, e y(t) é consequência) é:

11. Eixo horizontal de simetria

13. Semi-reta e coordenadas polares Em coordenadas polares , uma parábola com o foco na origem e topo no eixo x negativo é dada pela equação

14. onde l = 2 p é a distância do foco à parábola, medida através de uma linha perpendicular ao eixo. Note que esta é o dobro da distância do foco ao vertex da parábola ou a distância perpendicular do foco à diretriz. Forma em coordenadas gaussianas A forma em coordenadas gaussianas é dada por: (tan2φ,2tanφ) e possui a normal (cosφ,sinφ).

15. Aplicações práticas Em nosso dia-a-dia, as parábolas são utilizadas em diversos equipamentos e sistemas de vital importância para nossa sociedade. Dentre eles, podemos destacar:

16. Antenas parabólicas e Radares É comum observarmos no alto de residências e edifícios as Antenas Parabólicas, que captam ondas eletromagnéticas que são enviadas por satélites em órbita ao redor da terra. Isto somente é possível devido à propriedade da parábola de refletir o conjunto de raios recebidos em um único ponto (o foco da parábola). Neste ponto encontra-se posicionado o receptor de ondas, que enviará o sinal recebido para um conversor que as decodificará e enviará para o receptor de televisão. Os aparelhos de radar operam de forma semelhante às antenas parabólicas, recebendo o eco de pulsos eletromagnéticos.

17. Faróis de veículos Os refletores parabólicos de faróis e lanternas permitem que a luz da lâmpada localizada no foco se propague em raios paralelos ao eixo da parábola formando o facho. As lentes parabólicas posicionadas na parte de trás dos faróis dos veículos permitem que a luz gerada pelos mesmos seja direcionada para um ponto específico, o foco da parábola, que normalmente é apontado para o solo, evitando desta forma que a luz de um carro ofusque a visão de um motorista que venha em direção oposta.

18. Escola Estadual Edwads Corrêa e Souza Alunos:Carolina,Jeniffer,Itamar,Maria Carolina,Rhamon,Heloane, Samara 3° “A”