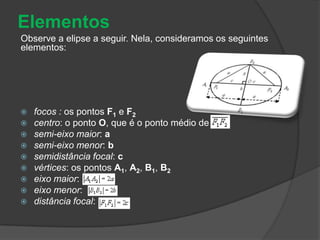
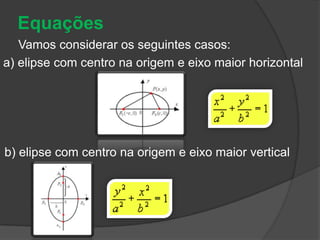
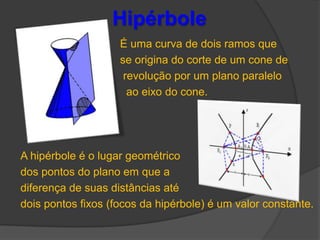
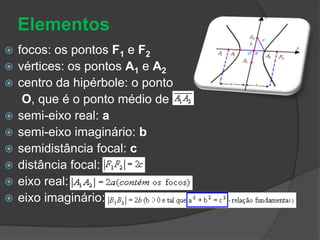
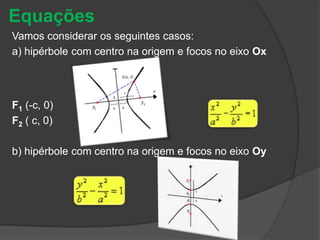
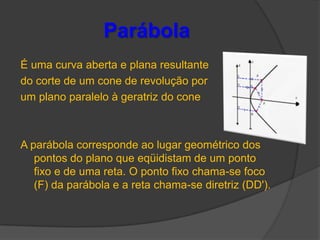
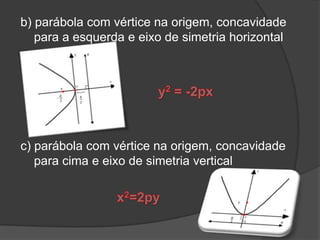
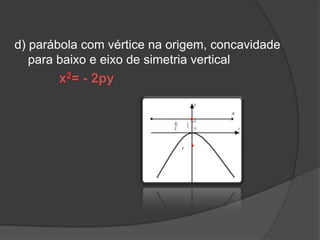
O documento descreve as três principais cônicas - elipse, hipérbole e parábola - definindo-as como lugares geométricos e apresentando seus elementos e equações características. A elipse é definida como o lugar onde a soma das distâncias até dois focos é constante, a hipérbole como a diferença das distâncias, e a parábola como o lugar onde a distância até um foco é igual à distância até uma reta fixa.

1. CÔNICAS COMO LUGAR GEOMETRICO Por: Profª Paula Patrícia

2. Quando você ouve falar em hipérbole, elipse e parábola pensa que estão falando grego. E estão mesmo. Foram os discípulos de Pitágoras (cerca de 540 a.C.) que usaram pela primeira vez estes termos, e é graças a eles que podemos descrever o desenho curvo que a luz projeta na parede, a parte espelhada da lâmpada de uma lanterna ou a superfície da água no copo, entre outras coisas. No século XVI, Johannes Kepler (1571 a 1630) demonstrou que a linha curva descrita por um planeta que gira ao redor do Sol é uma elipse, e Galileu Galilei (1584 a 1642) concluiu que a trajetória de um projétil é uma parábola. Essas descobertas tornaram mais evidente a importância do estudo desses tipos de curvas. ONDE ENCONTRAMOS ESSAS FIGURAS GEOMÉTRICAS?

3. UM POUCO DE HISTÓRIA O grego Apolônio (262 a.C. a 190 a.C.) utilizou o termo cônicas ao observar que estas curvas eram obtidas a partir de secções da superfície de um cone de folha dupla. Muito tempo mais tarde, com a criação da Geometria Analítica pelo francês René Descartes (1596 a 1662), as cônicas passaram a ser reconhecidas a partir de suas equações. A Geometria Analítica tem como idéia central a representação de pontos do espaço por meio de coordenadas. Um grande número de propriedades geométricas faz das curvas cônicas um instrumento adequado para diversas aplicações práticas.

4. Elipse É o lugar geométrico dos pontos do plano em que a soma de suas distâncias até dois pontos fixos (chamados focos) é constante. Uma forma simples de desenhar a elipse é fixar as extremidades de um fio (que deve ter um comprimento maior que a distância entre os dois focos) nos focos F e F' e, mantendo-o esticado, traçar com lápis uma linha, formando a elipse. A elipse também é definida como uma curva fechada plana que se produz quando um cone de revolução é cortado por um plano oblíquo a seu eixo

5. Observações: 1ª) A Terra descreve uma trajetória elíptica em torno do sol, que é um dos focos dessa trajetória. A lua em torno da terra e os demais satélites em relação a seus respectivos planetas também apresentam esse comportamento. 2ª) O cometa de Halley segue uma órbita elíptica, tendo o Sol como um dos focos. 3ª) As elipses são chamadas cônicas porque ficam configuradas pelo corte feito em um cone circular reto por um plano oblíquo em relação à sua base.

6. Elementos Observe a elipse a seguir. Nela, consideramos os seguintes elementos: focos : os pontos F1 e F2 centro: o ponto O, que é o ponto médio de semi-eixo maior: a semi-eixo menor: b semidistância focal: c vértices: os pontos A1, A2, B1, B2 eixo maior: eixo menor: distância focal:

7. Relação fundamental Na figura, aplicando o Teorema de Pitágoras ao triângulo OF2B2 , retângulo em O, podemos escrever a seguinte relação fundamental: a2 = b2 + c2

8. Excentricidade Chamamos de excentricidade o número real e tal que: e = c a Pela definição de elipse, 2c < 2a, então c < a e, conseqüentemente, 0 < e < 1. Observação:Quando os focos são muito próximos, ou seja, c é muito pequeno, a elipse se aproxima de uma circunferência.

9. Equações Vamos considerar os seguintes casos: a) elipse com centro na origem e eixo maior horizontal b) elipse com centro na origem e eixo maior vertical

10. Hipérbole É uma curva de dois ramos que se origina do corte de um cone de revolução por um plano paralelo ao eixo do cone. A hipérbole é o lugar geométrico dos pontos do plano em que a diferença de suas distâncias até dois pontos fixos (focos da hipérbole) é um valor constante.

11. Elementos focos: os pontos F1e F2 vértices: os pontos A1 e A2 centro da hipérbole: o ponto O, que é o ponto médio de semi-eixo real: a semi-eixo imaginário: b semidistância focal: c distância focal: eixo real: eixo imaginário:

12. Excentricidade Chamamos de excentricidade o número real e tal que: e = c a Como c > a, temos e > 1.

13. Equações Vamos considerar os seguintes casos: a) hipérbole com centro na origem e focos no eixo Ox F1 (-c, 0) F2 ( c, 0) b) hipérbole com centro na origem e focos no eixo Oy

14. Parábola É uma curva aberta e plana resultante do corte de um cone de revolução por um plano paralelo à geratriz do cone A parábola corresponde ao lugar geométrico dos pontos do plano que eqüidistam de um ponto fixo e de uma reta. O ponto fixo chama-se foco (F) da parábola e a reta chama-se diretriz (DD').

15. Observações: 1ª) A parábola é obtida seccionando-se obliquamente um cone circular reto: 2ª) Os telescópios refletores mais simples têm espelhos com secções planas parabólicas. 3ª) As trajetórias de alguns cometas são parábolas, sendo que o Sol ocupa o foco. 4ª) A superfície de um líquido contido em um cilindro que gira em torno de seu eixo com velocidade constante é parabólica.

16. Elementos foco: o ponto F diretriz: a reta d vértice: o ponto V parâmetro: p o vértice V e o foco F ficam numa mesma reta, o eixo de simetria e.

17. Equações Vamos considerar os seguintes casos: a) parábola com vértice na origem, concavidade para a direita e eixo de simetria horizontal y2 = 2px

18. b) parábola com vértice na origem, concavidade para a esquerda e eixo de simetria horizontal y2 = -2px c) parábola com vértice na origem, concavidade para cima e eixo de simetria vertical x2=2py

19. d) parábola com vértice na origem, concavidade para baixo e eixo de simetria vertical x2= - 2py

20. Bibliografia: Sites: www.somatematica.com.br www.klickeducacao.com.br Trabalho realizado para disciplina Informática Educativa II do curso de Pós-Graduação em Novas Tecnologia no Ensino da Matemática