Este documento apresenta informações sobre o livro "Cônicas e Quádricas" de Jacir J. Venturi. A obra contém 10 capítulos tratando de conceitos fundamentais de geometria analítica como parábolas, elipses, hipérboles e quádricas. O livro também fornece uma breve resenha histórica sobre o desenvolvimento das cônicas pelos matemáticos gregos desde a Escola Pitagórica até Apolônio.



























![Jacir. J. Venturi
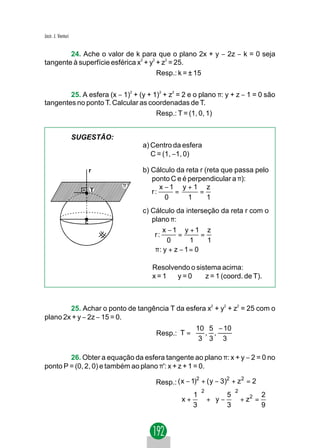
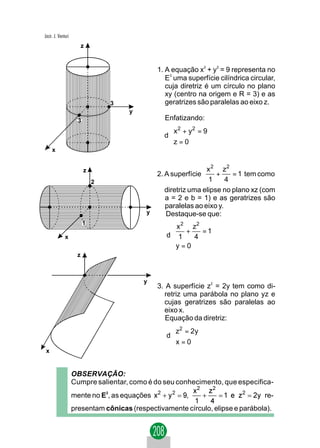
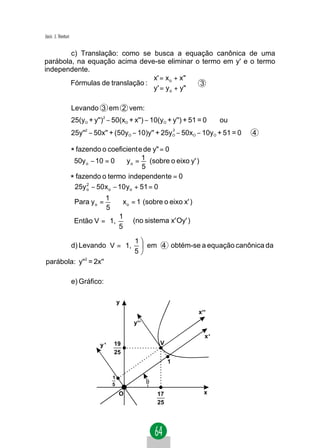
1. Dada a equação Ax2 + Bxy + Cy2 + Dx + Ey + F = 0, a transla-
ção não afeta os coeficientes dos termos do 2.º grau (A, B, C).
2. Após uma translação com O' = (xO, yO) o novo termo inde-
pendente F' pode ser obtido: F' = Ax2 + BxO yO + Cy2 + DxO + EyO + F.
O O
EXEMPLIFIQUEMOS:
Na equação 5x2 + 6xy + 5y2 − 4x + 4y + 8 = 0, os termos do 1.º grau
são eliminados quando feita uma translação para O' = (1, −1). Em relação
ao sistema x'O'y' a nova equação terá a forma 5x'2 + 6x'y' + 5y'2 + F' = 0.
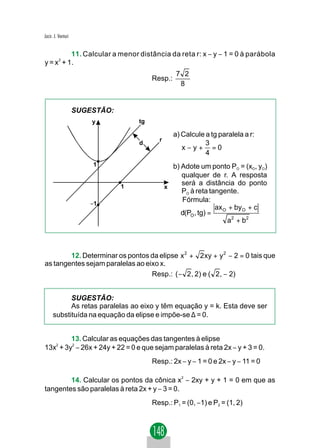
Mas, F' = 5(1)2 + 6(1) (−1) + 5(−1)2 − 4(1) − 4(−1) + 8 = 4.
Resp.: 5x'2 + 6x'y' + 5y'2 + 4 = 0
b) Pormeiodeumarotaçãoeliminarotermoemxy.
Dada a equação Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 ( 1 ), o termo
em xy pode ser eliminado mediante uma rotação de eixos correspon-
dente a umângulo θ tal que:
B
tg 2θ = (para A ≠ C)
A −C
DEMOSTRAÇÃO:
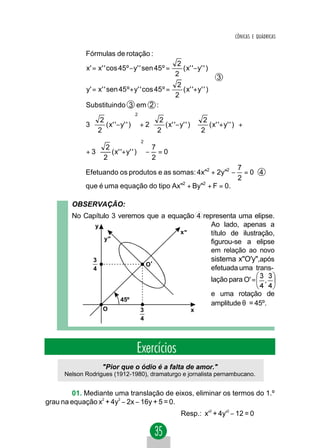
a) Fórmulas de rotação:
x = x' cos θ − y' sen θ
2
y = x' sen θ + y' cos θ
b) Substituindo 2 em 1 :
A(x' cos θ − y' sen θ) + B(x' cos θ − y' sen θ) (x' sen θ + y' cos θ) +
2
+ C(x' sen θ + y' cos θ)2 + ... = 0
ordenando os termos emx'2, y'2 e x' y':
(A cos2 θ + B sen θ cos θ + C sen2 θ)x'2 + [−2A sen θ cos θ +
+ B (cos2 θ − sen2 θ) + 2C sen θ cos θ] x' y' + (A sen2 θ −
− B sen θ cos θ + C cos2 θ)y'2 + ... = 0
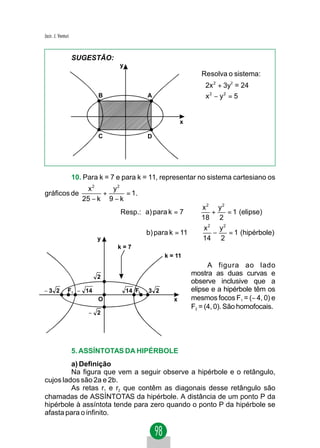
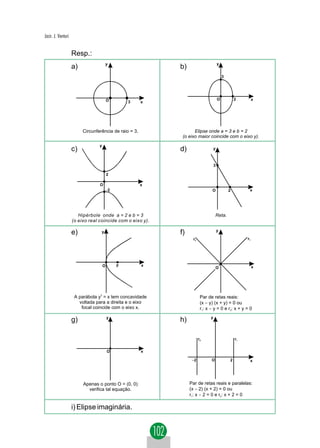
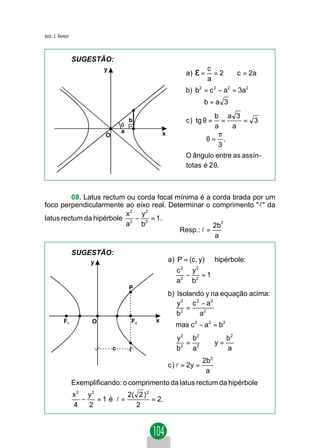
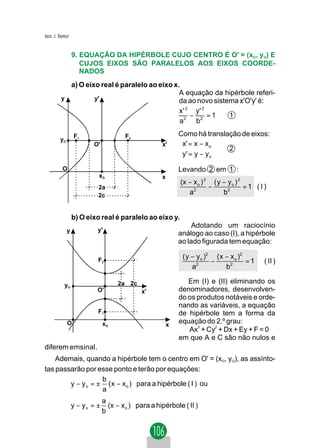
O termo em xy desaparecerá na equação acima se o seu coefici-
ente for nulo:](https://image.slidesharecdn.com/geometriaanaltica-121202104244-phpapp02/85/Geometria-analitica-30-320.jpg)

































































































![Jacir. J. Venturi
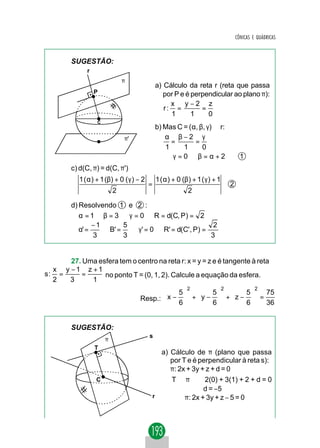
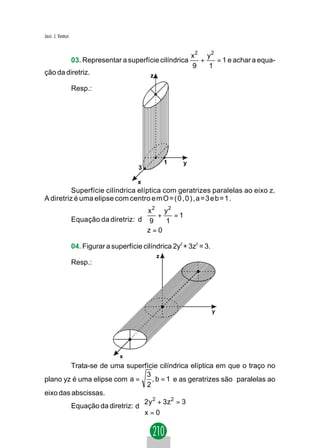
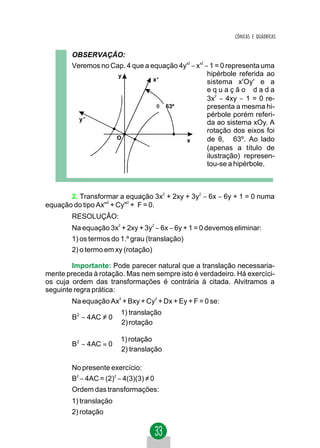
2.º PROBLEMA: EQUAÇÃO DA TANGENTE POR
UM PONTO EXTERNO À PARÁBOLA.
y tg Dados:
polar PO = (xO, yO)
y2 = 2px (parábola)
P1
A equação da tangente tem a
PO forma:
y − yO =m(x − xO) ou
x y = yO +m(x − xO) 1
P2 Levando-se 1 na equação da
parábola recai-se numa equação do
2.º grau. Nesta, impondo-se que o
discriminante ∆ = b − 4ac seja nulo,
2
tg obtém-se o(s) coeficiente(s) angu-
lar(es) m.
Os pontos P1 e P2 são os pontos de contato das tangentes com a
parábola. A reta P1P2 é cognominada reta polar de PO em relação à parábola.
Exercícios Resolvidos
"Se deres as costas à luz, nada mais verás
senão a tua própria sombra."
Zálkind Piategórsky
01. Obter as equações das tangentes à parábola x2 − y + 5 = 0
pelo ponto PO = (1, 2).
P1 a) Equação da tangente:
y
y − yO = m(x − xO)
y − 2 = m(x − 1)
ou
P2
y = m(x − 1) + 2 1
5
b) Substituindo-se 1 na equação da
2 PO parábola:
x2 − [m(x − 1) + 2] + 5 = 0
1 x desenvolvendo e ordenando:
t1
t2 x2 − mx + m + 3 = 0
c) Impondo ∆ = b2 − 4ac = 0
(−m)2 − 4.1.(m + 3) = 0
m2 − 4m − 12 = 0 ⇒ m = 6 ou m = −2](https://image.slidesharecdn.com/geometriaanaltica-121202104244-phpapp02/85/Geometria-analitica-150-320.jpg)


![CÔNICAS E QUÁDRICAS
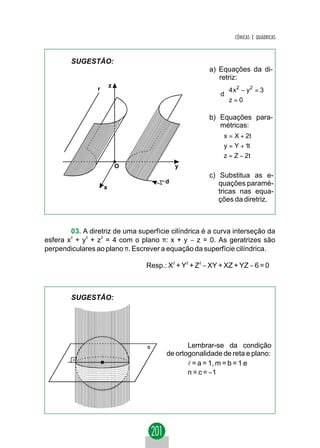
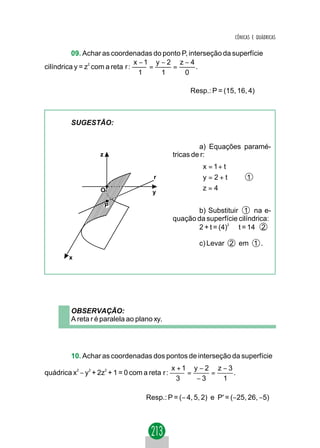
3.º PROBLEMA: EQUAÇÃO DA TANGENTE EM UM
PONTO PO = ( xO, yO) PERTENCENTE À PARÁBOLA.
Vamos determinar a equação da tangente à parábola y2 = 2px em
um ponto PO = (xO, yO) pertencente à parábola. A equação da tangente
procurada é do tipo y − yO =m(x − xO). y tg
DEDUÇÃO
Sejam: PO
y2 = 2px 1
y = y +m(x − x ) 2
O O
Levando 2 em 1 : x
[yO +m(x − xO)]2 = 2px
Efetuando o produto notável e
ordenando a equação do 2.º grau emx:
m2 x 2 + ( 2my O − 2m2 x O − 2p)x + y O − 2mx O y O + m2 x 2 = 0
2
O
Pela condição de tangência o discriminante deve anular-se:
∆ = b2 − 4ac = 0
( 2my O − 2m2 x O − 2p)2 − 4m2 ( y O − 2mx O y O + m2 x O ) = 0
2 2
Desenvolvendo e simplificando:
2m2xO − 2myO + p = 0
Aplicando a fórmula de Bháskara à equação acima (do 2.º grau
emm):
y O ± y 2 − 2px O
m= O
3
2xO
Mas como PO = (xO, yO) pertence à parábola:
y O = 2px O
2
4
Substituindo 4 em 3 :
y
m= O 5
2xO
Por seu turno 4 permite:
yO p p
= ⇒ =m 6
2xO yO yO](https://image.slidesharecdn.com/geometriaanaltica-121202104244-phpapp02/85/Geometria-analitica-153-320.jpg)