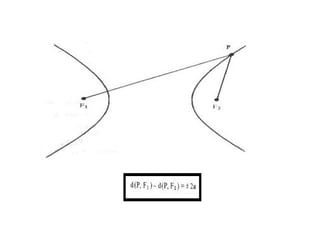
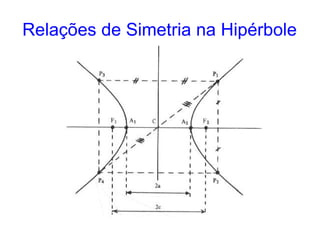
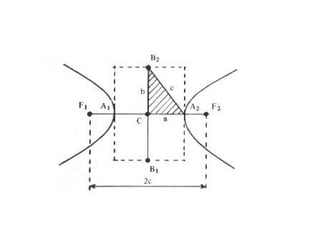
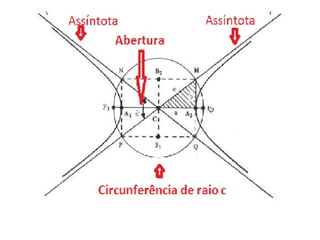
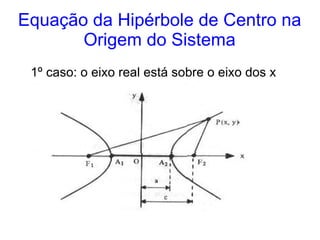
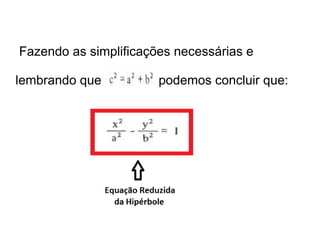
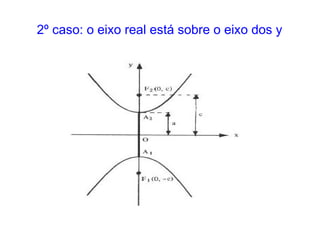
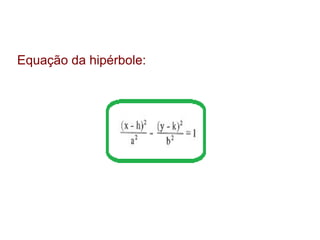
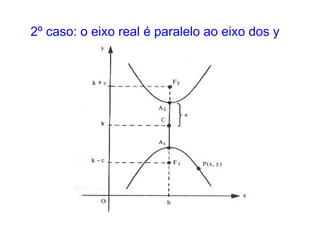
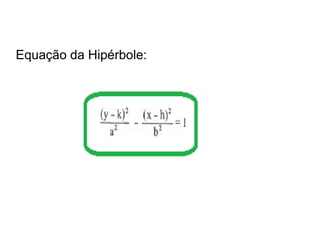
O documento descreve a hipérbole geométrica, definida como o lugar geométrico dos pontos cuja diferença absoluta das distâncias a dois pontos fixos, chamados de focos, é constante. Detalha os elementos da hipérbole, como focos, centro, eixos real e imaginário, vértices e excentricidade. Fornece as equações da hipérbole para diferentes posicionamentos do eixo real em relação aos eixos de coordenadas.

1. Universidade Federal do
Triângulo Mineiro – UFTM
Cônicas
Prof.: Daniel Oliveira Veronese

2. Hipérbole
Hipérbole é o lugar geométrico dos pontos de
um plano cuja diferença das distâncias, em
valor absoluto, a dois pontos fixos desse plano
é constante.
Consideremos no plano dois pontos distintos, F1
e F2, tal que a distância d(F1,F2)=2c. Seja a um
número real tal que 2a<2c.

3. Ao conjunto de todos os pontos P do plano tais
que:
dá-se o nome de hipérbole.

5. Relações de Simetria na Hipérbole

6. Elementos da Hipérbole
 Focos: são os pontos F1 e F2

Distância Focal: é a distância 2c entre os focos
 Centro: é o ponto médio C do seguimento F1 F2
 Eixo Real ou Transverso: é o seguimento A1A2
de comprimento 2a

Eixo Imaginário ou Conjugado: é o seguimento
 B1B2 de comprimento 2b
 Vértices: são os pontos A1 e A2

Excentricidade: é o número e(e>1) dado por:
e=c/a.

8. Observação
O valor de b é definido pela seguinte relação:

10. Observação
Mantendo o raio c da figura anterior e tomando
um valor para “a” menor do que o anterior, o
novo retângulo MNPQ será mais “estreito” e,
em consequência a abertura será maior.
Mas, diminuir o valor de “a” mantendo “c” fixo
significa significa aumentar o valor de e=c/a.
Assim, quanto maior for a excentricidade, maior
será a abertura.

11. Equação da Hipérbole de Centro na
Origem do Sistema
1º caso: o eixo real está sobre o eixo dos x

12. Da definição da hipérbole temos que:
ou seja:

13. Fazendo as simplificações necessárias e
lembrando que podemos concluir que:

14. 2º caso: o eixo real está sobre o eixo dos y

15. Nesse caso, a equação reduzida da hipérbole é
dada por:

16. Equação da Hipérbole de Centro
Fora da Origem do Sistema
1º caso: o eixo real é paralelo ao eixo dos x

17. Equação da hipérbole:

18. 2º caso: o eixo real é paralelo ao eixo dos y

19. Equação da Hipérbole:

20. Exemplos
Veja o seu caderno!!!!!!