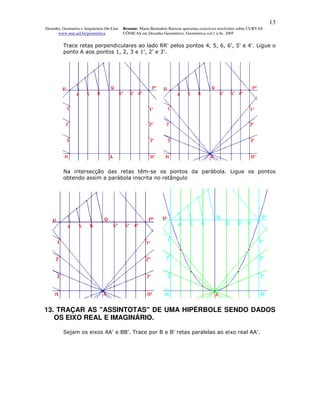
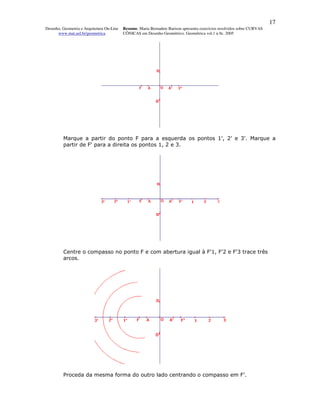
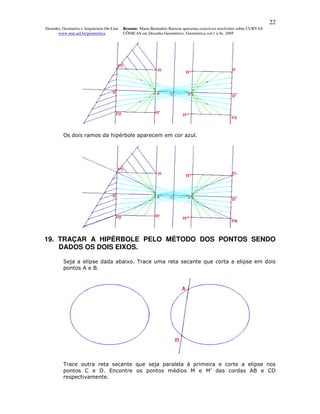
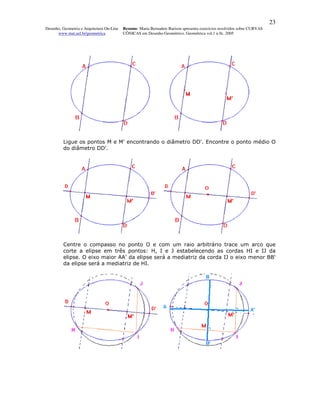
O documento apresenta 13 exercícios resolvidos sobre curvas cônicas, incluindo elipses, parábolas e hipérboles. Os exercícios demonstram vários métodos para traçar estas curvas, tais como utilizando os focos, círculos principais, pontos, retângulos e paralelogramos. O objetivo é fornecer exemplos passo-a-passo para que os leitores possam aprender a desenhar diferentes curvas cônicas.