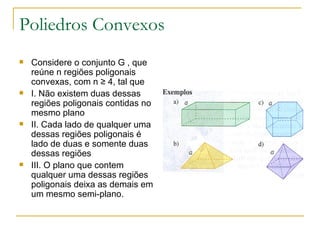
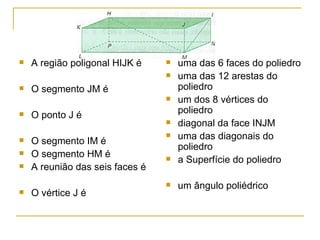
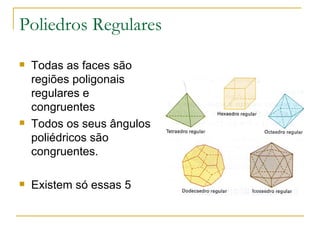
I. O documento descreve conceitos geométricos como regiões poligonais, poliedros convexos, elementos de um poliedro convexo como faces, arestas e vértices. II. Um poliedro é constituído por vinte ângulos triédricos. Para resolver quantas arestas possui, deve-se usar a fórmula de Euler. III. A fórmula de Euler relaciona o número de vértices, arestas e faces de um poliedro convexo.

1. AGORA TEM MATE‘MÁGICA’ Agora. Sim.. A melhor parte de toda a matemática.

2. Regiões poligonais A reunião de um polígono com seus pontos interiores, é chamada região poligonal. Essa região é chamada convexa se a reta que contem qualquer um dos lados do polígono, deixa todos os pontos da região poligonal num mesmo semi-plano

3. Poliedros Convexos Considere o conjunto G , que reúne n regiões poligonais convexas, com n ≥ 4, tal que I. Não existem duas dessas regiões poligonais contidas no mesmo plano II. Cada lado de qualquer uma dessas regiões poligonais é lado de duas e somente duas dessas regiões III. O plano que contem qualquer uma dessas regiões poligonais deixa as demais em um mesmo semi-plano.

4. Elementos de um Poliedro convexo As regiões poligonais de G são chamadas de faces do poliedro convexo. Cada lado de uma face é chamado de aresta do poliedro convexo. Cada vértice de uma faces, chama-se Vértice de poliedro convexo Qualquer diagonal de uma face é chamada de Diagonal de face Qualquer segmento de reta com extremos em dois vértices de faces diferente, recebe o nome de Diagonal do poliedro O conjunto G é chamado de superfície do poliedro Cada vértice de poliedro constitui um ângulo poliédrico

5. A região poligonal HIJK é O segmento JM é O ponto J é O segmento IM é O segmento HM é A reunião das seis faces é O vértice J é uma das 6 faces do poliedro uma das 12 arestas do poliedro um dos 8 vértices do poliedro diagonal da face INJM uma das diagonais do poliedro a Superfície do poliedro um ângulo poliédrico

6. Observe: Existem poliedros não convexos. Ângulos poliédricos e poliedros recebem nomes de acordo com o numero relacionado Exemplo. Um ângulo poliédrico com 5 arestas é chamada de ângulo pentaédrico. Um poliedro com 10 faces é chamado deca edro

7. Um poliedro é constituído por vinte ângulos triédricos. Quantas arestas possui este poliedro? Um octaedro possui todas as faces triangulares. quantas arestas possui esse poliedro?

8. Relação de Euler V + F = A + 2 Sendo v o numero de vértices, A o numero de Arestas e F o numero de faces Essa relação vale pra todos os poliedros convexos

9. Poliedros Regulares Todas as faces são regiões poligonais regulares e congruentes Todos os seus ângulos poliédricos são congruentes. Existem só essas 5