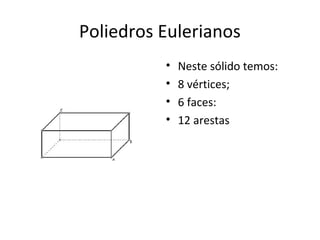
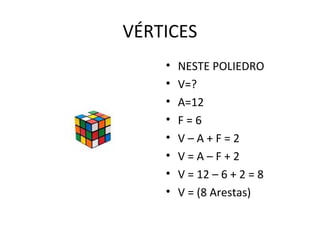
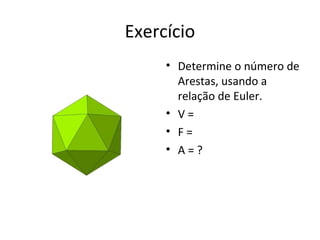
O documento discute vários sólidos geométricos, incluindo seu número de vértices, arestas e faces. Fornece detalhes sobre o cubo mágico, octaedro e esfera, e explica a relação de Euler que relaciona esses elementos.

1. SÓLIDOS GEOMÉTRICOS
• Cubo Mágico

2. Poliedros Eulerianos
• Neste sólido temos:
• 8 vértices;
• 6 faces:
• 12 arestas

3. SÓLIDOS GEOMÉTRICOS
• QUANTAS FACES?
• QUANTAS ARESTAS?
• QUANTOS VERTICES
OCTAEDRO

4. SÓLIDOS GEOMÉTRICOS
• O número de vértices?
• O número de arestas?
• E o número de Faces?

5. A Bola
• Quantas faces?
• Quantos Vértices?
• Quantas Arestas?

6. A relação de Euler
• V: Vértices; • Para todo poliedro
• A: Arestas; convexo é válida a
• F: faces; relação de Euler:
• V–A+F=2

7. VÉRTICES
• NESTE POLIEDRO
• V=?
• A=12
• F=6
• V–A+F=2
• V=A–F+2
• V = 12 – 6 + 2 = 8
• V = (8 Arestas)

8. Exercício
• Determine o número de
Arestas, usando a
relação de Euler.
• V=
• F=
• A=?

9. DESÁFIO
• Uma Bola possui 32
Faces (20 hexágonos e
12 pentágonos),
determine o numero de
arestas