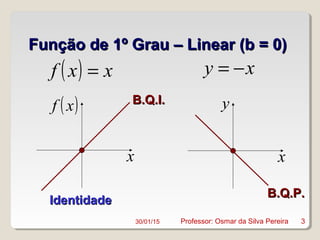
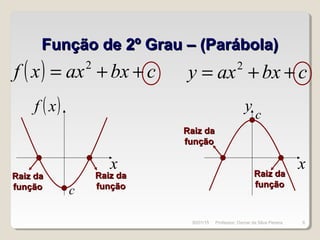
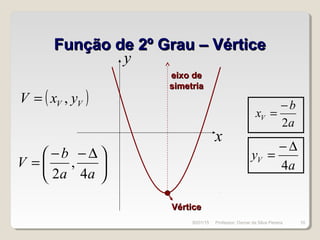
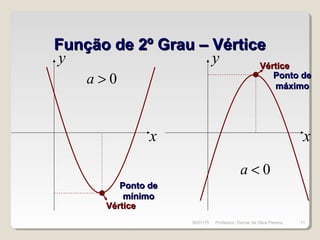
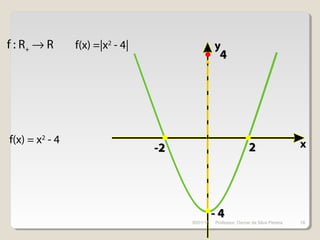
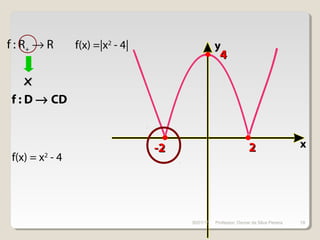
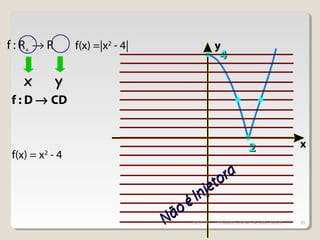
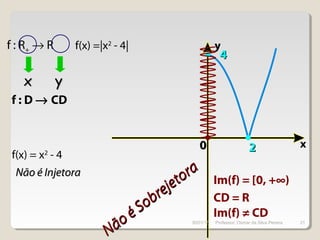
Este documento discute conceitos fundamentais de funções do 1o e 2o grau, incluindo: (1) equações de funções lineares e parabólicas, (2) propriedades como crescimento/decrescimento e concavidade, (3) raízes e vértice de funções quadráticas, e (4) noções de função inversa e composição.














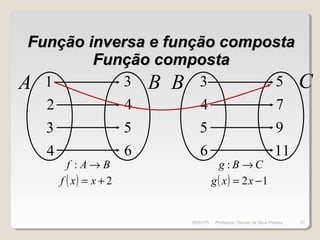
![Função inversa e função compostaFunção inversa e função composta
Função compostaFunção composta
( ) ( )[ ]xfgxh =CAh →:
( ) ( ) 12 −⋅= xfxh
( ) ( ) 122 −+⋅= xxh
( ) 142 −+= xxh
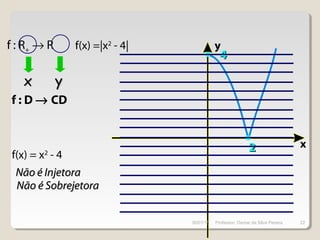
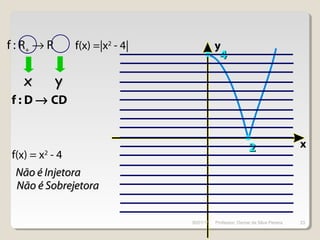
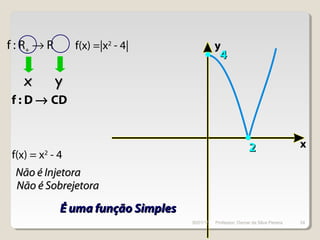
( ) 32 += xxh
( ) 12 −= xxg ( ) 2+= xxf
( ) ( ) 32 +== xxfgxh
30/01/15 32Professor: Osmar da Silva Pereira](https://image.slidesharecdn.com/matematica-funo-pptsalvoautomaticamente-101117110923-phpapp01/85/Matematica-funcao-ppt-salvo-automaticamente-32-320.jpg)
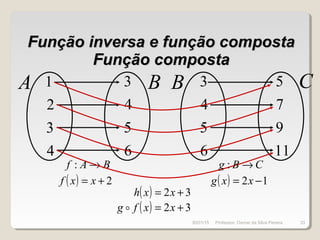
![Função inversa e função compostaFunção inversa e função composta
Função compostaFunção composta
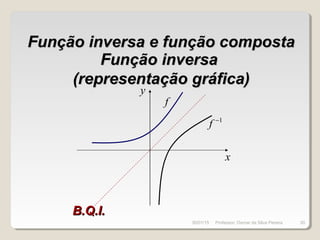
A
B
Cf
g
fgh =
( ) ( )[ ]xfgxh =
( ) ( )xfgxh =
fgh =
x f
30/01/15 34Professor: Osmar da Silva Pereira](https://image.slidesharecdn.com/matematica-funo-pptsalvoautomaticamente-101117110923-phpapp01/85/Matematica-funcao-ppt-salvo-automaticamente-34-320.jpg)

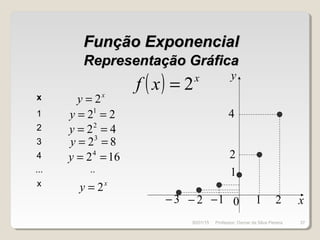
![Função ExponencialFunção Exponencial
RRf →:
DefiniçãoDefinição
RDomínioDomínio
( ) ] [+∞= ,0Im f
ImagemImagem
( ) x
axf = 10 ≠< a
*
+R
( ) ( )+∞= ,0Im f
( ) RfD =
30/01/15 36Professor: Osmar da Silva Pereira](https://image.slidesharecdn.com/matematica-funo-pptsalvoautomaticamente-101117110923-phpapp01/85/Matematica-funcao-ppt-salvo-automaticamente-36-320.jpg)


















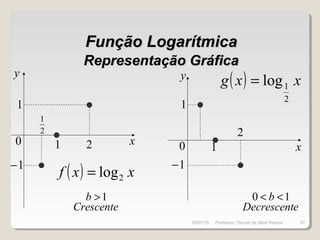




![Inequação LogarítmicaInequação Logarítmica
( ) ( )xgxf bb loglog ≥
1>b
( ) ( )xgxf ≥
10 << b
( ) ( )xgxf ≤
( ) 5log3log 22 >−x
53 >−x
8>x
03 >−x
C.EC.E
3>x
{ }8/ >∈= xRxS
] [+∞= ,8S
30/01/15 63Professor: Osmar da Silva Pereira](https://image.slidesharecdn.com/matematica-funo-pptsalvoautomaticamente-101117110923-phpapp01/85/Matematica-funcao-ppt-salvo-automaticamente-63-320.jpg)



