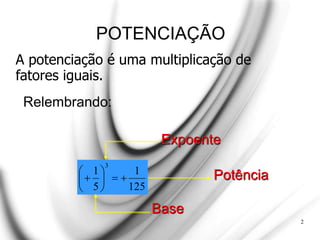
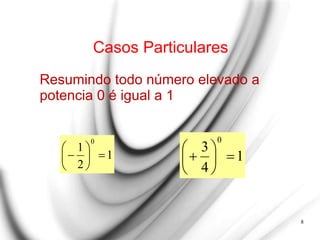
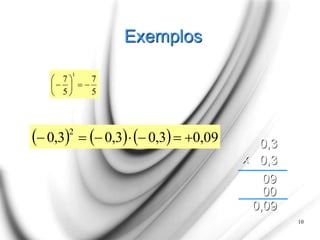
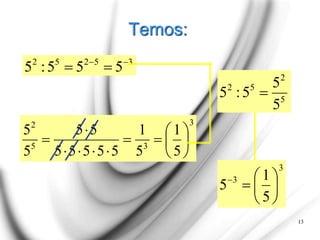
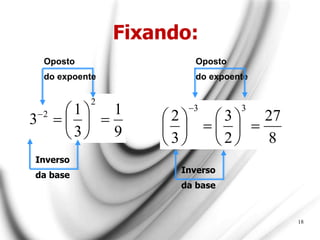
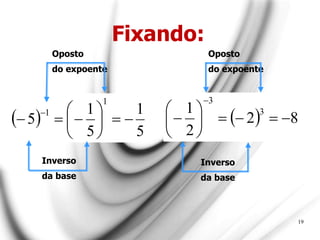
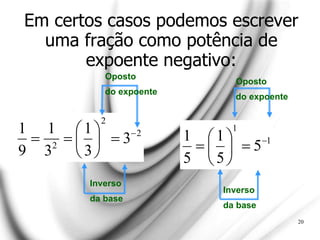
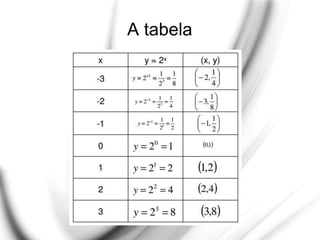
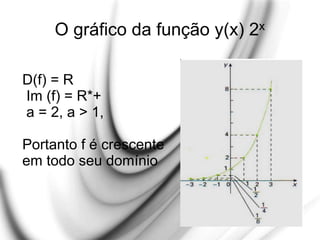
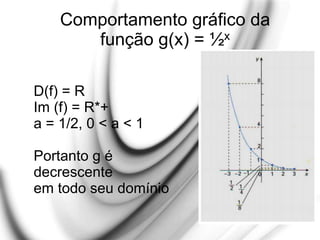
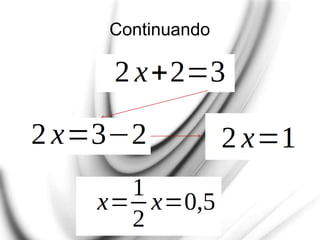
O documento apresenta uma explicação detalhada sobre potenciação e funções exponenciais, abordando conceitos fundamentais como bases, expoentes e suas propriedades. Exemplos são fornecidos para ilustrar diferentes casos, como potências com expoentes pares e ímpares, assim como a aplicação de potências de base negativa. Além disso, o texto trata do comportamento das funções exponenciais em termos de crescimento ou decrescimento, dependendo do valor da base.

1. POTENCIAÇÃO E
FUNÇÃO EXPONENCIAL
prof. André Aparecido da Silva
anndrepr@yahoo.com.br
1

2. POTENCIAÇÃO
125
1
5
1
3









2
A potenciação é uma multiplicação de
fatores iguais.
Relembrando:
Expoente
Base
Potência

3. POTENCIAÇÃO
3
Exemplo:
• 210  2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
x 2 x 2 = 1024
• 34  3 x 3 x 3 x 3 = 81
•

4. Lembre-se
25
4
5
2
5
2
5
2
2

























4
1
16
81
2
3
2
3
2
3
2
3
2
3
4









































Quando o expoente é par, a potência
é sempre positiva.

5. Lembre-se
8
1
2
1
2
1
2
1
2
1
3

































5
2
27
8
3
2
3
2
3
2
3
2
3

































Quando o expoente é ímpar, a
potência tem o mesmo sinal da base.

6. Casos Particulares
2
1
2
1
1









6
3
3
2
3
2
1









Expoente 1: As potências de expoente
1 são iguais a base.

7. Casos Particulares
1
5
8
0








7
4
1
4
7
0








Expoente Zero: As potências de expoente
zero são iguais a 1.

8. Casos Particulares
1
2
1
0








8
1
4
3
0








Resumindo todo número elevado a
potencia 0 é igual a 1

9. Outros Exemplos
25
49
5
7
2









9
64
343
4
7
3









9
1
3
1
2









27
125
3
5
3










10. Exemplos
5
7
5
7
1









10
      09
,
0
3
,
0
3
,
0
3
,
0
2






 0,3
0,3
x
09
00
0,09

11. Potência com
Expoente Inteiro
Negativo
11

12. Considere o Quociente:
12
3
5
2
5
2
5
5
5
:
5 



5
2
5
:
5
Pela propriedade do quociente de potência
de mesma base temos:
Escrevendo o quociente em forma de fração
temos:
3
3
5
2
5
1
5
1
5
5
5
5
5
5
5
5
5















13. Temos:
13
3
5
2
5
2
5
5
5
:
5 



3
3
5
2
5
1
5
1
5
5
5
5
5
5
5
5
5














5
2
5
2
5
5
5
:
5 
3
3
5
1
5 








14. Resumindo
14
Na divisão de potencias de mesma
base, podemos preservar a base e
diminuir os expoentes...

15. EXEMPLOS
15
• 5³ / 5² = 53-2= 5¹ = 5
•1012 / 104 =1012-4 =108
• 65 / 6² = 65-2= 63 = 216

16. Note ainda que:
16
 
 
  3
1
3
3
3
3
1
3
1
3
3
5
1
5
5
1
5
1
5
5
5
5






















Isso significa que pode ser interpretado
como inverso de
  1
3
5

3
5

17. Conclusão
A potência com expoente
negativo de um número
racional diferente de zero é
igual a uma outra potência que
tem a base igual ao inverso da
base anterior e o expoente
igual ao oposto do expoente
anterior.
17

18. Fixando:
18
9
1
3
1
3
2
2









Inverso
da base
Oposto
do expoente
8
27
2
3
3
2
3
3















Inverso
da base
Oposto
do expoente

19. Fixando:
19
  8
2
2
1 3
3












Inverso
da base
Oposto
do expoente
 
5
1
5
1
5
1
1












Inverso
da base
Oposto
do expoente

20. Em certos casos podemos escrever
uma fração como potência de
expoente negativo:
20
2
2
2
3
3
1
3
1
9
1 









Inverso
da base
Oposto
do expoente
1
1
5
5
1
5
1 








Inverso
da base
Oposto
do expoente

21. Exemplos:
21
5
5
5
10
10
1
10
1
100000
1
00001
,
0 










2
2
2
2
2
2
5
10
10
5
10
5
100
25
25
,
0 


















3
3
3
2
2
3
8
27



















22. Propriedades
As propriedades da
potenciação estudadas
são válidas também
para potências com
expoente inteiro
negativo.
22

23. Exemplos
23
3
2
5
2
5
3
2
3
2
3
2
3
2































  5
6
1
6
1
6
1
4
5
4
5
4
5
4
5
:
4
5













































  6
3
2
3
2
2
3
2
3
2
3




































24. 1 24
Potencia com base negativa
Antes,
Que tal lembrarmos das regras de sinais!
Observe:
▬ sinal negativo + sinal positivo
Lembre-se:
Multiplicação de sinais diferentes, resultado negativo.
Multiplicação de sinais iguais, resultado positivo.

25. 1 25
Potencia com base negativa
O cálculo de potências com base negativa
é semelhante ao de base positiva.
Exemplos:
(-4)2
= (- 4) .(- 4)
=
+16
Expoente par.
Base
Potência
a)
b)(-3)4 = (-3) .(-3) .(-3) .(-3)
=
+81
Toda potência de base negativa e expoente par, é um
número inteiro positivo.

26. 1 26
Potencia com base negativa
O cálculo de potências com base negativa
é semelhante ao de base positiva.
Exemplos:
(-5)3 = (-5).
=
-125
Expoente ímpar.
Base
a)
b)
Potência
(-1)5
=(-1). (-1). (-1).
(-5).
(-1).
=
-1
Toda potência de base negativa e expoente ímpar, é um
número inteiro negativo.
(-5)
(-1)
x

27. 1 27
Potencia com base negativa
Por convenção, adotamos as regras:
Exemplos:
O EXPOENTE 1
Toda potência de expoente 1 é sempre igual à base.
a)(+9)1
=+9
b)(-13)1
=-13
c) (0)1
= 0
d)(-10)1
= -10

28. 1 28
Potencia com base negativa
Por convenção, adotamos as regras:
Exemplos:
O EXPOENTE 0 (zero)
Toda potência de expoente 0 (zero) e base diferente de 0
(zero) é igual à 1.
a) = 1
(-14)0
b)(+27)0
= 1
c)(-9)0
= 1
d) (-530)0
= 1

29. 1 29
Potencia com base negativa
Devemos dar atenção a duas situações de
significados e valores diferentes.
Exemplos:
(-4)2
= (-4). (-4) +16
a) =
(-4)2 significa o quadrado de -4.
- 42
= - 4. 4 -16
b) =
-42 significa o oposto do quadrado de 4.
Logo: (- 4)2 ≠ - 42

30. 1 30
Potencia com base negativa
Sempre que trabalhar com potências, tenha
atenção as suas propriedades, regras e
sinais.
Conclusão:

31. CUIDADO!!!!
Um abuso muito vulgar, é
apresentar números que aumentam
com o adjetivo sensacionalista de
“crescimento exponencial”
 É muito provável que 90% das
pessoas não sabem o que significa
verdadeiramente essa expressão.

32. Xadrez e Exponenciação

33. 1 33
Função Exponencial

34. Continuando
• f(x) = 2x é uma função
exponencial.
Por meio de uma tabela, podemos
obter alguns pontos da função e, a
partir deles, esboçar o gráfico.

35. A tabela

36. O gráfico da função y(x) 2x
D(f) = R
Im (f) = R*+
a = 2, a > 1,
Portanto f é crescente
em todo seu domínio

37. Comportamento do gráfico da
função exponencial
Através função exponencial
g(x) = ½x e usando uma
tabela, podemos obter alguns
pontos da função e, a partir
deles, esboçar o gráfico.

38. A tabela da função g(x) = ½x

39. Comportamento gráfico da
função g(x) = ½x
D(f) = R
Im (f) = R*+
a = 1/2, 0 < a < 1
Portanto g é
decrescente
em todo seu domínio

40. Resumindo...
Tendo a função f(x) = ax, se “a” for
maior que 1 a função será crescente,
se “a” for maior que zero e menor que
1 a função será decrescente

41. Outro Exemplo

42. Resolvendo o Exemplo

43. Resolvendo o Exemplo

44. Resolvendo o exemplo

45. Resolvendo o exemplo

46. Resolvendo o exemplo

47. Resolvendo o exemplo

48. Resolvendo o exemplo

49. Resolvendo o exemplo

50. Questão...
Como ficaria o gráfico desta função
f(x) = 3x+1 ?

51. Equação Exponencial

52. Vamos a resolução
Nossa equação agora é
4x2+ 4x = 412
Aqui as bases são iguais, logo,
posso cortar e trabalhar só com os
expoentes...

53. Vamos a resolução
4x2+ 4x = 412
Temos agora a seguinte equação
x2+ 4x =12.
Colocando o 12 para outro lado da
igualdade teremos
x2+ 4x -12 = 0 (A = 1, B = 4 e C = 12 )

54. Resolvendo com Bhaskara
x2+ 4x -12 = 0 (A = 1, B = 4 e C = 12 )

55. Resolvendo com Bhaskara
x2+ 4x -12 = 0 (A = 1, B = 4 e C = 12 )

56. Resolvendo com Bhaskara

57. Outro Exemplo
Vamos primeiramente deixar todos
os termos em bases iguais, para isto
basta decompor 8 em fatores iguais,
então o 8 poderá ser escrito como
23 .

58. Continuando
Como todas as bases são iguais,
agora podemos cortar as bases e
trabalhar só com os expoentes.

59. Continuando

60. Continuando

61. Continuando

62. Substituindo na equação

63. Terminando a equação

64. Agora um exemplo com frações

65. Agora um exemplo com frações

66. Agora um exemplo com frações
Para inverter numerador e denominador
vou deixar com a potencia negativa

67. Agora um exemplo com frações
Agora cortando as bases teremos…

68. 68
Material elaborado pelo:
Prof. André Aparecido da Silva
Disciplina Matemática.
Disponível no site: www.oxnar.com.br/