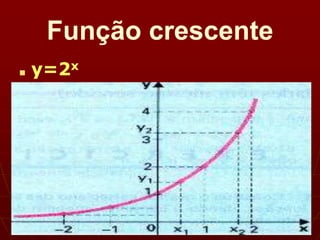
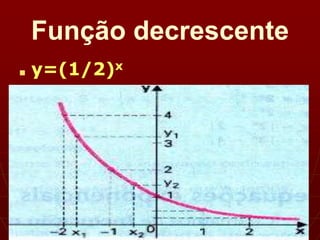
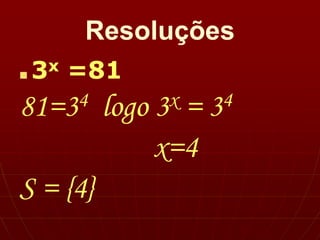Este documento define funções exponenciais como aquelas onde a variável aparece em expoente. A função f(x)=ax, com a∈IR+ e a≠1, é chamada função exponencial de base a. O gráfico de funções exponenciais depende se a>1 ou 0<a<1, podendo ser crescente ou decrescente. Equações exponenciais são resolvidas reduzindo-as à mesma potência e aplicando a propriedade de que potências iguais têm expoentes iguais.

1. Função Exponencial
Prof@. Alessandra de Oliveira

2. Definição
■ Chamamos de
funções
exponenciais
aquelas nas quais
temos a variável
aparecendo em
expoente.
■ A função f:IR🡪IR+
definida por
f(x)=ax, com a ∈
IR+ e a≠1, é
chamada função
exponencial de
base a.

3. Domínio e Contradomínio
■ O domínio dessa função é
o conjunto IR (reais) e o
contradomínio é IR+
(reais positivos, maiores
que zero).

4. GRÁFICO CARTESIANO DA
EXPONENCIAL
■ Temos 2 casos a considerar:
🡪 quando a>1;
Exemplo: y=2x (nesse caso, a=2, logo
a>1)
🡪 quando 0<a<1.
Exemplo: y=(1/2)x (nesse caso, a=1/2,
logo 0<a<1)

5. Função crescente
■ y=2x

6. Função decrescente
■ y=(1/2)x

7. Características Gráficas
■ o gráfico nunca intercepta o
eixo horizontal; a função não
tem raízes;
■ o gráfico corta o eixo vertical
no ponto (0,1);
■ os valores de y são sempre
positivos, portanto o conjunto
imagem é Im=IR+.

8. EQUAÇÕES EXPONENCIAIS
■ Para resolver equações exponenciais,
devemos realizar dois passos
importantes:
■ 1º) redução dos dois membros da
equação a potências de mesma base;
■ 2º) aplicação da propriedade:

9. Exemplos de equações
■ 3x =81 (x=4)
■ 9x = 1
■ 23x-1 = 322x

10. Resoluções
■ 3x =81
81=34 logo 3x = 34
x=4
S = {4}

11. Resoluções
■ 9x = 1
9x = 1 ⇒ 9x = 90 ; logo x=0.
S = {0}

12. Resoluções
■ 23x-1 = 322x
23x-1 = 322x
23x-1 = (25)2x
23x-1 = 210x
3x-1=10x
x=-1/7 S = {-1/7 }