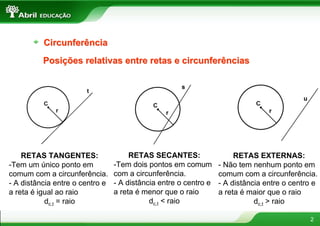
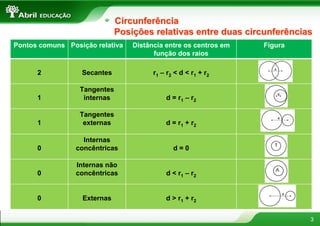
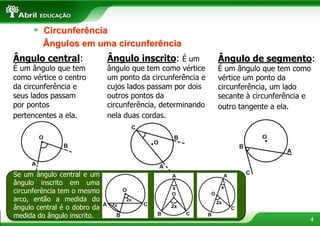
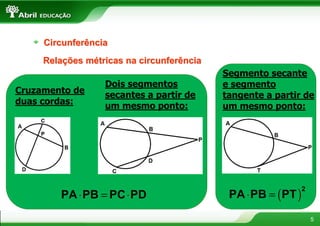
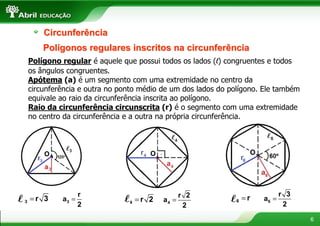
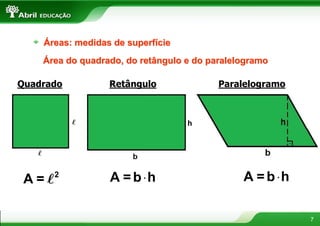
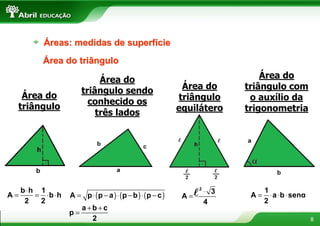
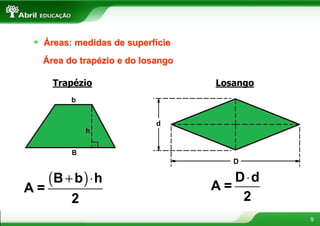
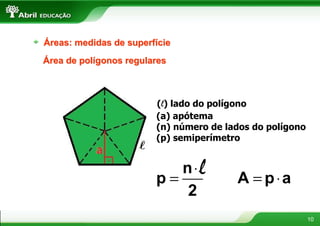
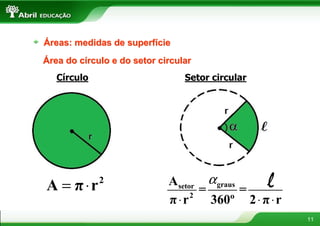
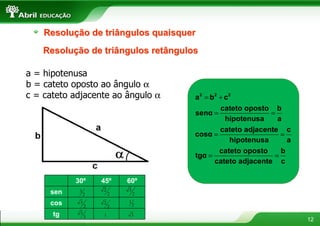
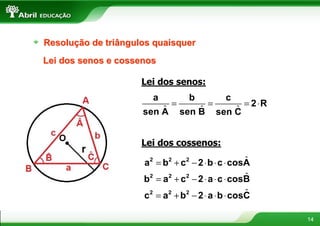
1) O documento discute conceitos geométricos como circunferência, áreas de figuras planas e resolução de triângulos. 2) Inclui informações sobre circunferência, áreas do quadrado, retângulo, triângulo, trapézio e círculo. 3) Apresenta métodos para resolução de triângulos retângulos e uso da lei dos senos e cossenos.

1. Circunferência, áreas e resolução de triângulos quaisquer
Slides
Circunferência
Áreas: medidas de superfície
Resolução de triângulos quaisquer:
resolução de triângulos retângulos
Resolução de triângulos quaisquer:
lei dos senos e lei dos cossenos
Esquadros de madeira – www.ser.com.br
Internet
Trigonometria
1

2. Circunferência
Posições relativas entre retas e circunferências
RETAS TANGENTES: RETAS SECANTES: RETAS EXTERNAS:
-Tem um único ponto em -Tem dois pontos em comum - Não tem nenhum ponto em
comum com a circunferência. com a circunferência. comum com a circunferência.
- A distância entre o centro e - A distância entre o centro e - A distância entre o centro e
a reta é igual ao raio a reta é menor que o raio a reta é maior que o raio
dc,t = raio dc,t < raio dc,t > raio
2

3. Circunferência
Posições relativas entre duas circunferências
Pontos comuns Posição relativa Distância entre os centros em Figura
função dos raios
2 Secantes r1 – r2 < d < r1 + r2
Tangentes
1 internas d = r1 – r2
Tangentes
1 externas d = r1 + r2
Internas
0 concêntricas d=0
Internas não
0 concêntricas d < r1 – r2
0 Externas d > r1 + r2
3

4. Circunferência
Ângulos em uma circunferência
Ângulo central: Ângulo inscrito: É um Ângulo de segmento:
É um ângulo que tem ângulo que tem como vértice É um ângulo que tem como
como vértice o centro um ponto da circunferência e vértice um ponto da
da circunferência e cujos lados passam por dois circunferência, um lado
seus lados passam outros pontos da secante à circunferência e
por pontos circunferência, determinando outro tangente a ela.
pertencentes a ela. nela duas cordas.
Se um ângulo central e um
ângulo inscrito em uma
circunferência tem o mesmo
arco, então a medida do
ângulo central é o dobro da
medida do ângulo inscrito.
4

5. Circunferência
Relações métricas na circunferência
Segmento secante
Dois segmentos e segmento
Cruzamento de secantes a partir de tangente a partir de
duas cordas: um mesmo ponto: um mesmo ponto:
PA ⋅ PB = (PT )
2
PA ⋅ PB = PC ⋅ PD
5

6. Circunferência
Polígonos regulares inscritos na circunferência
Polígono regular é aquele que possui todos os lados (l) congruentes e todos
os ângulos congruentes.
Apótema (a) é um segmento com uma extremidade no centro da
circunferência e outra no ponto médio de um dos lados do polígono. Ele também
equivale ao raio da circunferência inscrita ao polígono.
Raio da circunferência circunscrita (r) é o segmento com uma extremidade
no centro da circunferência e a outra na própria circunferência.
r r 2 r 3
l 3 =r 3 a3 = l 4 =r 2 a4 = l 6 =r a6 =
2 2 2
6

7. Áreas: medidas de superfície
Área do quadrado, do retângulo e do paralelogramo
Quadrado Retângulo Paralelogramo
A=l 2
A = b ⋅h A = b ⋅h
7

8. Áreas: medidas de superfície
Área do triângulo
Área do Área do
triângulo sendo Área do triângulo com
Área do triângulo o auxílio da
conhecido os
triângulo equilátero trigonometria
três lados
b ⋅h 1 l2⋅ 3 1
A= = ⋅b ⋅h A = p ⋅ (p − a ) ⋅ (p − b ) ⋅ (p − c ) A= A= ⋅ a ⋅ b ⋅ senα
2 2 4 2
a +b +c
p=
2 8

9. Áreas: medidas de superfície
Área do trapézio e do losango
Trapézio Losango
A=
(B + b ) ⋅ h A=
D⋅d
2 2
9

10. Áreas: medidas de superfície
Área de polígonos regulares
(l) lado do polígono
(a) apótema
(n) número de lados do polígono
(p) semiperímetro
n ⋅.
l
p= A = p⋅a
2
10

11. Áreas: medidas de superfície
Área do círculo e do setor circular
Círculo Setor circular
A = π ⋅r 2 A setor α graus l
= =
π ⋅r 2
360º 2 ⋅ π ⋅ r
11

12. Resolução de triângulos quaisquer
Resolução de triângulos retângulos
a = hipotenusa
b = cateto oposto ao ângulo α
c = cateto adjacente ao ângulo α a2 = b2 + c2
cateto oposto b
senα = =
hipotenusa a
cateto adjacente c
cosα = =
hipotenusa a
cateto oposto b
tgα = =
cateto adjacente c
30º 45º 60º
2 3
sen 1
2 2 2
cos 3 2 1
2 2 2
tg 3 1 3
3
12

13. Resolução de triângulos quaisquer
Seno e cosseno de ângulos obtusos
É necessário saber que:
sen 90º = 1 e cos 90º = 0
Senos de ângulos obtusos são exatamente iguais
aos senos dos suplementos desses ângulos:
sen x = sen (180º - x)
Cossenos de ângulos obtusos são opostos aos
cossenos dos suplementos desses ângulos:
cos x = - cos (180º - x)
13

14. Resolução de triângulos quaisquer
Lei dos senos e cossenos
Lei dos senos:
a b c
= = = 2 ⋅R
ˆ
sen A ˆ
sen B ˆ
sen C
Lei dos cossenos:
a2 = b2 + c 2 − 2 ⋅ b ⋅ c ⋅ cosAˆ
b2 = a 2 + c 2 − 2 ⋅ a ⋅ c ⋅ cosB
ˆ
ˆ
c2 = a2 + b2 − 2 ⋅ a ⋅ b ⋅ cosC
14