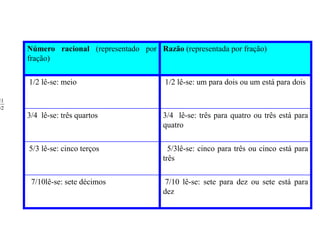
O documento explica os conceitos de razão e proporção matemática. Apresenta que uma razão é representada por uma fração que indica a relação entre dois números, sendo o antecedente e o conseqüente. Também define proporção como a igualdade entre duas ou mais razões e apresenta propriedades fundamentais como o produto dos extremos ser igual ao produto dos meios.

1. Professor Walisson Grangeiro

2. Razão e Proporção
Razão: é o quociente indicado (exato)
entre dois números racionais, sendo que o
segundo número é diferente de zero.
Como você pode perceber, uma razão
é representada por uma fração. No entanto,
não deve ser lida como se fosse um número
racional. Observe o quadro abaixo:

3. Número racional (representado por Razão (representada por fração)
fração)
1/2 lê-se: meio 1/2 lê-se: um para dois ou um está para dois
31
42
3/4 lê-se: três quartos 3/4 lê-se: três para quatro ou três está para
quatro
5/3 lê-se: cinco terços 5/3lê-se: cinco para três ou cinco está para
três
7/10lê-se: sete décimos 7/10 lê-se: sete para dez ou sete está para
dez

4. OS TERMOS DE UMA RAZÃO: O
ANTECEDENTE E O CONSEQÜENTE
3
Vamos considerar a notação . O que
5
ela representa?
3
A notação 5 é um numeral (fração) que
representa um número “três quintos”,
onde 3 é o numerador, e 5, o
denominador.
3
Porém, 5 é a representação também
da razão “três para cinco”, onde 3 é o
antecedente, e 5, o conseqüente.

5. RAZÕES EQUIVALENTES
Ao multiplicar ou dividir os termos de
uma razão por um mesmo número
diferente de zero, obtém-se outra razão
equivalente à primeira.
Veja o exemplo:
3 6 9 12
4 8 12 16
48 24 12 4
Forma Irredutível
60 30 15 5

6. PROPORÇÃO
A proporção é uma igualdade entre
duas ou mais razões.
Quando temos a igualdade só de duas
razões , chamamos essa igualdade de
proporção simples.
Se tivermos a igualdade de mais de
duas razões , chamamos de proporção
contínua.

7. Desta forma temos que:
x 2
Pr oporção simples
y 5
x y z
Pr oporção contínua
4 5 3

8. Propriedade Fundamental
A propriedade fundamental da
proporção diz que o produto dos
extremos é igual ao produto dos
meios.
a c
axd bxc
b d

9. Exemplos:
1) Dois números estão na razão de 2 para 3.
Acrescentando-se 2 a cada um, as somas estão
na razão de 3 para 5. Então, o produto dos dois
números é:
a) 90
b) 96
c) 180
d) 72
e) -124

10. Solução:
x 2 x 2 3
e que
y 3 y 2 5
x y
a x 2.a e a y 3a
2 3
substituindo os valores de x e y na outra proporção temos :
2a 2 3
(2a 2) x 5 (3a 2 ) x3
3a 2 5
10a 10 9a 6 10a 9a 6 10 a 4
substituindo o valor de a em x e y temos :
x 2 . ( 4) 8 ; y 3.( 4) 12 log o x . y 96

11. 2) Sabendo que x + y = 42, determine x e
y na proporção .
x 5
e x y 42
y 9
x y
a x 5.a e a y 9a
5 9
substituindo os valores de x e y na outra proporção temos :
42
x y 42 5a 9 a 42 14a 42 a 3
14
substituindo o valor de a em x e y temos :
x 5 . (3) 15 ; y 9 .(3) 27

12. 3) A soma da idade do pai e do filho é
45 anos. A idade do pai está para a idade
do filho, assim como 7 está para 2.
Determine a idade do pai e do filho.
P 7
e P F 45
F 2

13. P F
a P 7.a e a F 2a
7 2
substituindo os valores de P e F na outra proporção temos :
45
P F 45 7a 2a 45 9a 45 a 5
9
substituindo o valor de a em P e F temos :
P 7 . (5) 35 ; F 2 .(5) 10

14. Porcentagem
Introdução:
Utilizamos o cálculo de porcentagem
constantemente no nosso cotidiano. Dois
simples exemplos:
1) Uma loja lança uma promoção de
10% no preço dos seus produtos. Se uma
mercadoria custa R$120,00, quanto a
mercadoria passará a custar?

15. O desconto será de 10% do valor de
R$120,00. Logo:
10 1200
120 x 12
100 100
Retiramos, portanto, R$12,00 de
R$120,00: 120 - 12 = 108
Passaremos a pagar, com a promoção,
R$108,00.

16. 2) Uma sala de aula possui 100 alunos,
sendo que 40% são meninas. Qual a
quantidade de meninas e de meninos?
quantidade de meninas será:
40 4000
100 x 40
100 100
E a de meninos será: 100 - 40 = 60.

17. Razão centesimal:
Como o próprio nome já diz, é a fração
cujo denominador é igual a 100.
Exemplos:
( lê-se 10 por cento)
(lê-se 150 por cento)

18. Definição de taxa porcentual ou
porcentagem:
As expressões 7%, 16% e 125% são
chamadas taxas centesimais ou taxas
percentuais.
Porcentagem é o valor obtido ao
aplicarmos uma taxa percentual a um
determinado valor.

19. Exemplos:
Calcular 10% de 300.
Calcular 25% de 200kg.

20. Um jogador de futebol, ao longo de um
campeonato, cobrou 75 faltas,
transformando em gols 8% dessas faltas.
Quantos gols de falta esse jogador fez?

21. Exercícios
Qual a razão que é igual a 2/7 e cujo
antecedente seja igual a 8.

22. Solução:
Vamos igualar as razões.
8=2
X 7
2x = 8 x 7
2x = 56
X = 56/2
X = 28
Desta forma a razão igual a 2/7, com antecedente igual
a 8 é : 8/28 = 2/7

23. 2) Em uma sala de aula, a razão de
moças para o número de rapazes é de
5/4. Se o número total de alunos desta
turma é de 45 pessoas, caso exista uma
festa quantas moças ficariam sem par ?

24. Solução:
Primeiro vamos denominar o número de moças por X, e o número de rapazes por Y.
x/y = 5/4 (Igualam-se as razões)
x + y = 45 (Soma total de alunos)
x + y = 5 + 4 (Aplicação das propriedades das proporções)
x 5
45/x = 9/5
45 x 5 = 9x
225 = 9x ---> x = 225/9 ---> x = 25 moças
Substituindo X = 25 na expressão x + y = 45, temos :
25 + y = 45 ---> y = 45 – 25 ----> y = 20 rapazes
Tendo por base que cada rapaz fique apenas com uma moça, o número de moças que ficariam sem
par será : 25 – 20 = 5 moças
Então, o número de moças que ficará sem par é igual a 5.

25. 3) A razão das idades de duas pessoas é
2/3. Achar estas idades sabendo que sua
soma é 35 anos.
a)14 e 20 anos
b)14 e 21 anos
c)15 e 20 anos
d)18 e 17 anos
e)13 e 22 anos

26. Solução:
a 2
; a b 35
b 3
a b
x a 2.x ; x b 3x
2 3
substituindo os valores de a e b na outra proporção temos :
35
a b 35 2 x 3x 35 5x 35 x 7
5
substituindo o valor de x em a e b temos :
a 2. (7) 14 ; b 3.(7) 21

27. 4) A diferença dos volumes de dois
sólidos é 9cm³ e a sua razão é 2/3. Achar
os volumes.
a)17cm³ e 28cm³
b)18cm³ e 27cm³
c)19cm³ e 28cm³
d)20cm³ e 27cm³
e)n.d.a

28. Solução:
a 2
; b a 9
b 3
a b
x a 2.x ; x b 3x
2 3
substituindo os valores de a e b na outra proporção temos :
b a 9 3x 2 x 9 x 9
substituindo o valor de x em a e b temos :
a 2. (9) 18 ; b 3.(9) 27

29. 5) O preço de uma casa sofreu
um aumento de 20%, passando a ser
vendida por 35 000 reais. Qual era o
preço desta casa antes deste aumento?

30. Solução:
Porcentagem Preço
120 35 000
100 x

31. 6) Aumentando-se 10% uma grandeza
positiva x e do resultado diminui-se 10%
obtemos:
(A) x
(B) 0,9·x
(C) 0,99·x
(D) 1,1·x
(E) 1,2·x

32. Solução:
Acrescentar 10% em X significa dizer
que x passa a ser 1,1 x.
Retirar 10% de 1,1x é igual: 0,11
Logo :
1,1x – 0,11x = 0,99x

33. 7) Com o reajuste de 10% no preço da
mercadoria A, seu novo preço
ultrapassará o da mercadoria B em
R$9,99. Dando um desconto de 5% no
preço da mercadoria B, o novo preço
dessa mercadoria se igualará ao preço da
mercadoria A antes do reajuste de 10%.
Assim, o preço da mercadoria B, sem o
desconto de 5%, em R$, é

34. Solução:
Temos:
1,1 A = B + 9,99 e que 0,95 B = A
1,1( 0,95 B ) = B + 9,99
1,045 B = B + 9,99
1,045B – B = 9,99
0,045B = 9,99
B = R$ 222,00