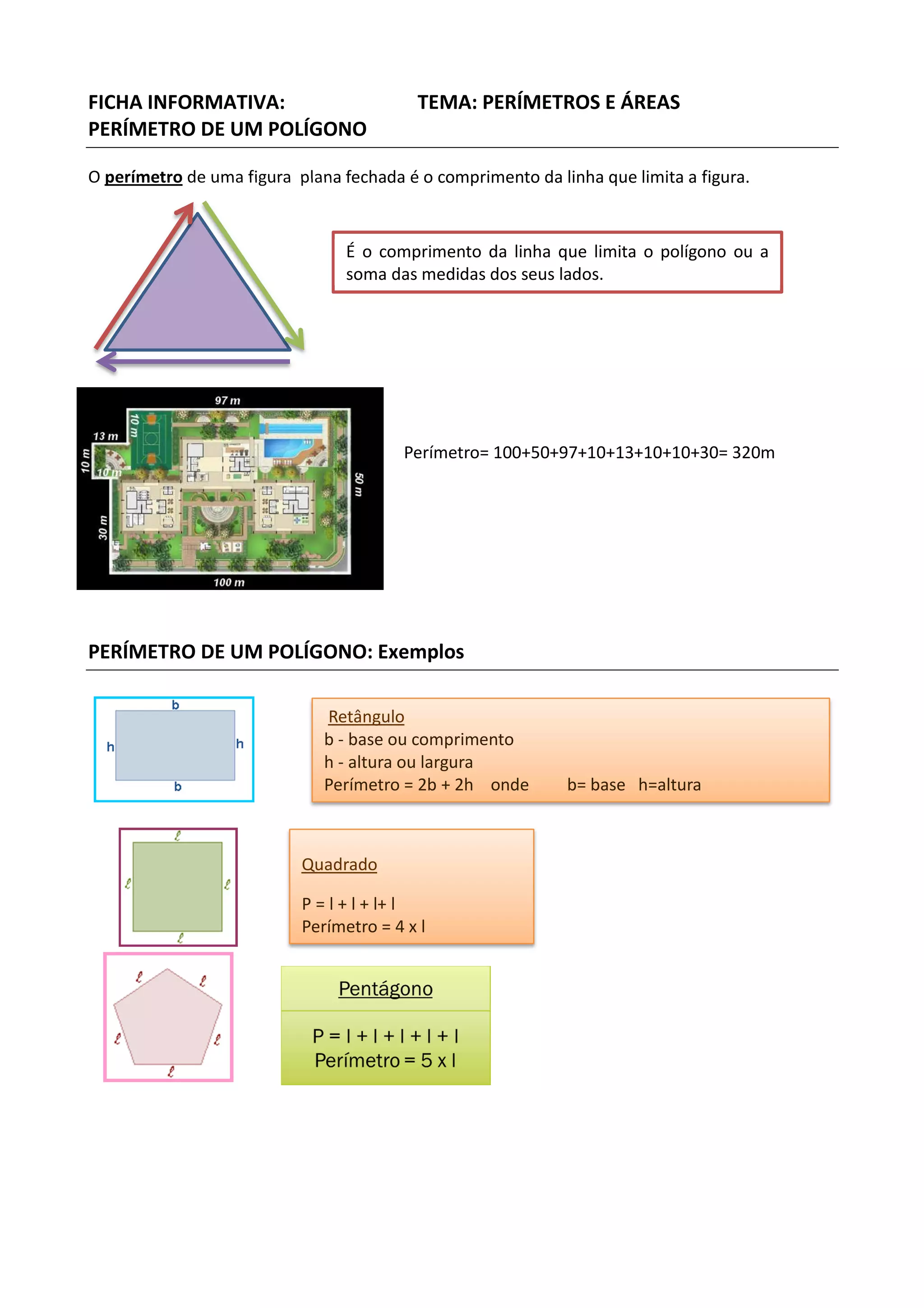
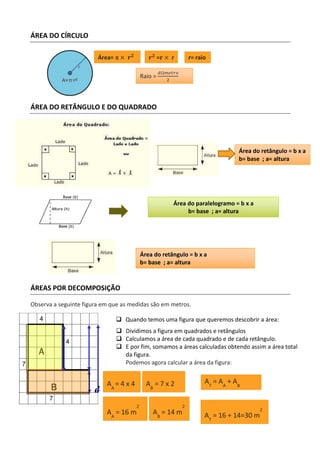
[1] O documento fornece informações sobre perímetros e áreas de polígonos, círculos, retângulos e quadrados, incluindo fórmulas para calcular suas medidas. [2] É explicado que o perímetro é a medida da linha que delimita a figura e a área é a quantidade de espaço dentro da figura. [3] Vários exemplos ilustram como calcular perímetros e áreas de diferentes figuras geométricas.