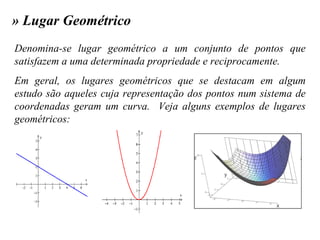
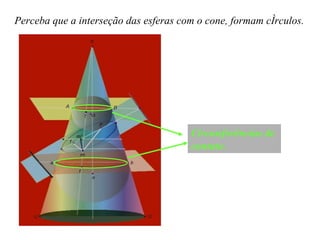
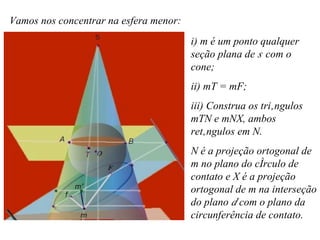
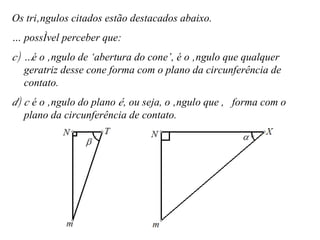
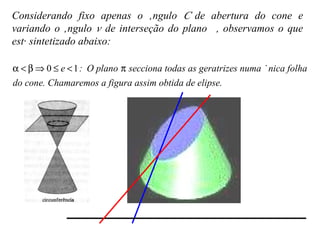
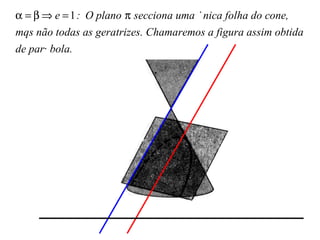
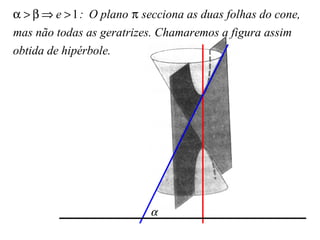
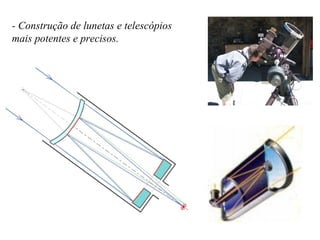
O documento aborda as seções planas de um cone circular reto, destacando a contribuição histórica de Apolônio de Perga e suas influências em diversos cientistas. Ele define 'lugares geométricos' e explora as propriedades das cônicas, com aplicações em astronomia, engenharia, arquitetura e tecnologia. O texto também fornece links para recursos adicionais e referências bibliográficas para estudo aprofundado.

1. Seções Planas do Cone Circular Reto Professor Amorim Informática Educativa II – Especialização em Novas Tecnologias no Ensino da Matemática

2. » Um Pouco de História Estudos sobre o tema que veremos aqui aparecem na história da humanidade antes mesmo de Euclides ( 325 – 265a.C.). Um nome que merece destaque é Apolonio de Perga (262 – 190a.C.), pois produziu uma série de oito livro sobre o assunto, “Seções Cônicas”, apesar do oitavo volume ter se perdido. Esta coleção veio a influenciar muito outros expoentes das ciências como Ptolomeu, Kepler, Galileu, Isaac Newton e outros.

3. » Lugar Geométrico Denomina-se lugar geométrico a um conjunto de pontos que satisfazem a uma determinada propriedade e reciprocamente. Em geral, os lugares geométricos que se destacam em algum estudo são aqueles cuja representação dos pontos num sistema de coordenadas geram um curva. Veja alguns exemplos de lugares geométricos:

4. » Secção Plana de um Cone Circular Reto Imaginemos um cone circular reto ilimitado. Seja  um plano que seccione todas as geratrizes do cone uma única vez. No interior desse cone e tangenciando o cone e o plano  , vamos construir esferas conforme o exemplo a seguir: Você pode visualizar e manipular a figura ao lado com o programa “CtrlView” e abrindo, com ele a figura ‘cone1’ em: http://www.4shared.com/file/174995108/2fccb8d7/cone1.html Brinque também com as outras formas que estão lá: http://www.4shared.com/file/175078272/4e3c4597/cone3.html http://www.4shared.com/file/175078290/3eb10935/cone2.html

5. Perceba que a interseção das esferas com o cone, formam círculos. Circunferências de contato.

6. Vamos nos concentrar na esfera menor: i) m é um ponto qualquer seção plana de  com o cone; ii) mT = mF; iii) Construa os triângulos mTN e mNX, ambos retângulos em N. N é a projeção ortogonal de m no plano do círculo de contato e X é a projeção ortogonal de m na interseção do plano  com o plano da circunferência de contato.

7. Os triângulos citados estão destacados abaixo. É possível perceber que:  é o ângulo de ‘abertura do cone’, é o ângulo que qualquer geratriz desse cone forma com o plano da circunferência de contato.  é o ângulo do plano  , ou seja, o ângulo que  forma com o plano da circunferência de contato.

8. Considerando, inicialmente, esses ângulos fixos, ou seja, sem variarmos as inclinações, teremos: Essa constante ‘e’ recebe o nome de excentricidade.

9. Considerando fixo apenas o ângulo  de abertura do cone e variando o ângulo  de interseção do plano  , observamos o que está sintetizado abaixo:  

10.  

11.  

12. Estas figuras recebem o nome de cônicas. Ao longo da história da humanidade, o homem tem encontrado diversas aplicações úteis com base nas propriedades dessas figuras. Veja: - Estudo das órbitas dos planetas em torno do Sol e trajetória de cometas:

13. - Construção de antenas mais eficientes, as antenas parabólicas. Construção de faróis que aproveitam o máximo das lâmpadas.

14. - Refletores odontológicos e aparelhos de radioterapia.

15. - Construção de lunetas e telescópios mais potentes e precisos.

16. - Na arquitetura: Acústica e na engenharia. Catedral de São Paulo. Colisseu Golden Gate

17. Para conhecer mais sobre as cônicas, suas propriedades e aplicações, veja alguns links: Faculdade de Ciências de Lisboa: http://www.educ.fc.ul.pt/icm/icm2000/icm27/ UFRJ: http://www.im.ufrj.br/dmm/projeto/diversos/conicas.html Jocelino Sato – Universidade Federal de Uberlândia 2004: http://www.4shared.com/file/175024073/b88991a7/Conicas_JocelinoSato.html Síntese dos livros de Apolônio: http://www.educ.fc.ul.pt/docentes/opombo/seminario/apolonio/conicas.htm

18. Referências Bibliográficas: » Boyer, C. B. História da Matemática. Editora Edgar Blücher Ltda. São Paulo: 1974. » Lehmann, C. H. Geometria Analítica. Editora Globo. São Paulo: 1998. » Revista do Professor de Matemática, IMPA-SBM, Rio de Janeiro.