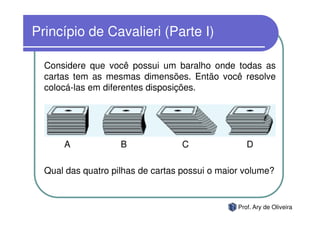
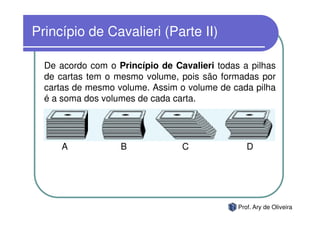
O documento discute geometria espacial, especificamente o volume de prismas. Explica o princípio de Cavalieri, como calcular o volume de um prisma multiplicando a área da base pela altura, e fornece exercícios de fixação resolvidos para o cálculo do volume de diferentes prismas.

1. Geometria Espacial (Volume do Prismas)
Princípio de Cavalieri; Volume do Prisma (V);
Exercícios de Fixação.
Prof. Ary de Oliveira

2. Princípio de Cavalieri (Parte I)
Considere que você possui um baralho onde todas as
cartas tem as mesmas dimensões. Então você resolve
colocá-las em diferentes disposições.
A B C D
Qual das quatro pilhas de cartas possui o maior volume?
Prof. Ary de Oliveira

3. Princípio de Cavalieri (Parte II)
De acordo com o Princípio de Cavalieri todas a pilhas
de cartas tem o mesmo volume, pois são formadas por
cartas de mesmo volume. Assim o volume de cada pilha
é a soma dos volumes de cada carta.
A B C D
Prof. Ary de Oliveira

4. Volume do Prisma
Afinal de contas como calculamos o volume de um
prisma?
Simples, basta você multiplicar a área da base (AB) do
prisma pela sua altura (h). Assim obtemos a seguinte
expressão:
V = AB h
Prof. Ary de Oliveira

5. Exercício de Fixação 01
Uma caixa d’água foi construída em uma residência de
alvenaria e o dono da casa deseja saber o seu volume.
Supondo que a caixa d’água tem a forma de um prisma
reto de base quadrangular com 1 metros de largura, 2
metros de comprimento e 1,5 metros de altura. Qual o
seu volume em litros (Lembre-se que 1 L = 1 dm3)?
1,5 m
1m 2m
Prof. Ary de Oliveira

6. Exercício de Fixação 01
Uma caixa d’água foi construída em uma residência de
alvenaria e o dono da casa deseja saber o seu volume.
Supondo que a caixa d’água tem a forma de um prisma
reto de base quadrangular com 1 metros de largura, 2
metros de comprimento e 1,5 metros de altura. Qual o
seu volume em litros (Lembre-se que 1 L = 1 dm3)?
SOLUÇÃO
1,5 m
AB = 10 ⋅ 20 ⇒ AB = 200 dm 2
1m 2m
V = 200 ⋅ 15 ⇒ V = 3000 dm3 ⇒ V = 3000 L
Prof. Ary de Oliveira

7. Exercício de Fixação 02
(UFPI) A base de um prisma reto é um triângulo cuja
hipotenusa mede 5 cm e um dos catetos mede 3 cm. Se
a medida da altura desse prisma é 10 cm, seu volume,
em centímetros cúbicos, mede:
(A) 60
(B) 70
(C) 80
(D) 90
(E) 100
Prof. Ary de Oliveira

8. Exercício de Fixação 02
(UFPI) A base de um prisma reto é um triângulo cuja
hipotenusa mede 5 cm e um dos catetos mede 3 cm. Se
a medida da altura desse prisma é 10 cm, seu volume,
em centímetros cúbicos, mede:
(A) 60 SOLUÇÃO
(B) 70 52 = b 2 + 32 ⇒ b 2 = 16 ⇒ b = 4 cm
(C) 80
3⋅ 4
(D) 90 AB = ⇒ AB = 6 cm 2
(E) 100 2
V = 6 ⋅ 10 ⇒ V = 60 cm3
Prof. Ary de Oliveira