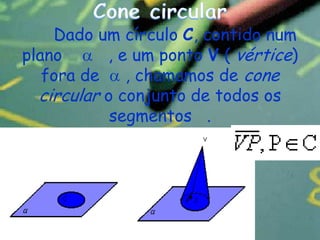
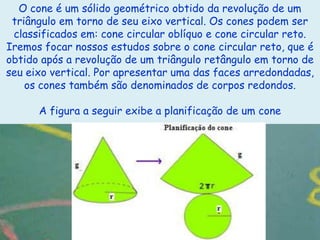
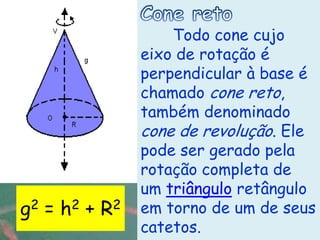
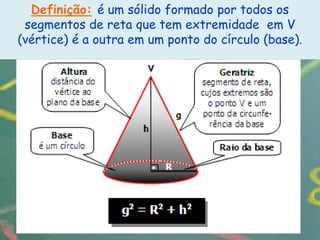
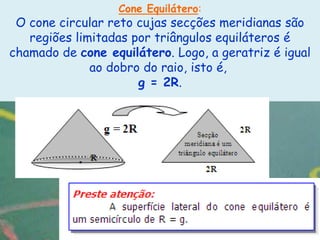
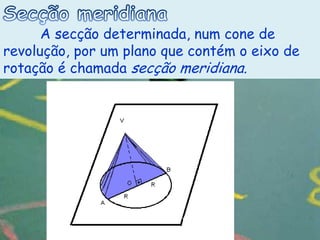
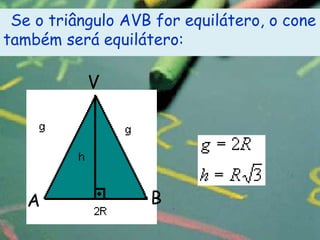
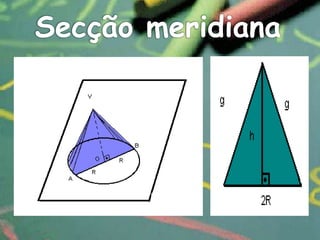
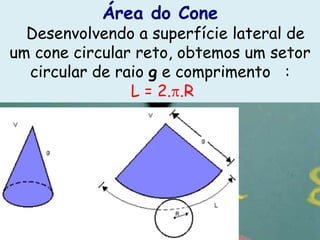
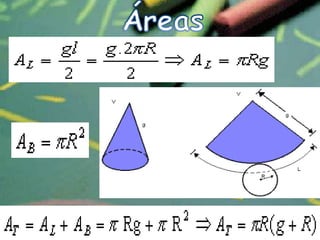
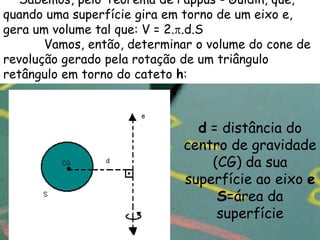
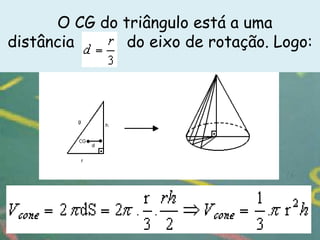
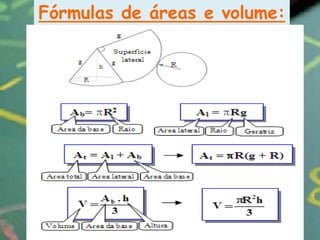
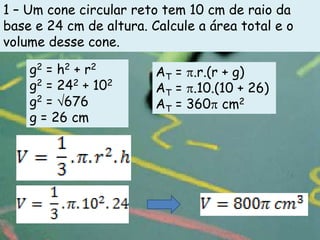
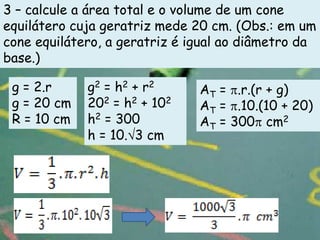
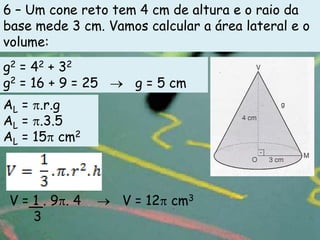
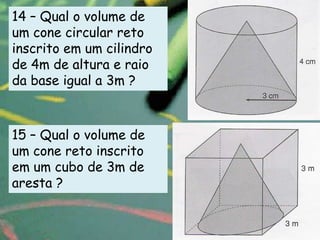
O documento apresenta definições e propriedades geométricas do cone circular reto, incluindo suas partes constituintes, fórmulas para calcular área total, área lateral e volume. Há também exemplos resolvidos de cálculos envolvendo estas grandezas para diferentes cones retos.

2. Cones no trânsito...

3. E mais ao
sul do País
uma linda
catedral
em forma
de cone.

4. À noite e
iluminada.

5. Dado um círculo C, contido num
plano , e um ponto V ( vértice)
fora de , chamamos de cone
circular o conjunto de todos os
segmentos .

7. • altura: distância h do vértice V ao plano
• geratriz (g):segmento com uma
extremidade no ponto V e outra num
ponto da circunferência
• raio da base: raio R do círculo
• eixo de rotação:reta determinada pelo
centro do círculo e pelo vértice do cone

8. Elementos do cone circular
Dado o cone a seguir, consideramos os seguintes
elementos:
•altura: distância h do vértice V ao plano
•geratriz (g):segmento com uma extremidade no
ponto V e outra num ponto da circunferência
•raio da base: raio R do círculo
•eixo de rotação:reta determinada pelo centro do
círculo e pelo vértice do cone

9. O cone é um sólido geométrico obtido da revolução de um
triângulo em torno de seu eixo vertical. Os cones podem ser
classificados em: cone circular oblíquo e cone circular reto.
Iremos focar nossos estudos sobre o cone circular reto, que é
obtido após a revolução de um triângulo retângulo em torno de
seu eixo vertical. Por apresentar uma das faces arredondadas,
os cones também são denominados de corpos redondos.
A figura a seguir exibe a planificação de um cone

10. Todo cone cujo
eixo de rotação é
perpendicular à base é
chamado cone reto,
também denominado
cone de revolução. Ele
pode ser gerado pela
rotação completa de
um triângulo retângulo
g2 = h2 + R2 em torno de um de seus
catetos.

11. Definição: é um sólido formado por todos os
segmentos de reta que tem extremidade em V
(vértice) é a outra em um ponto do círculo (base).

12. Cone Equilátero:
O cone circular reto cujas secções meridianas são
regiões limitadas por triângulos equiláteros é
chamado de cone equilátero. Logo, a geratriz é igual
ao dobro do raio, isto é,
g = 2R.

13. A secção determinada, num cone de
revolução, por um plano que contém o eixo de
rotação é chamada secção meridiana.

14. Se o triângulo AVB for equilátero, o cone
também será equilátero:
V
A B

16. Área do Cone
Desenvolvendo a superfície lateral de
um cone circular reto, obtemos um setor
circular de raio g e comprimento :
L = 2. .R

17. Assim, temos de considerar as seguintes
áreas:
a) área lateral (AL): área do setor circular
AL = .R.g
b) área da base (AB):área do circulo do raio R
AB = .R2
c) área total (AT):soma da área lateral com a
área da base
AT = AL + AB = Rg + R2 AT = R.(g + R)

19. Exemplo 1. Calcule a área total de um cone cujo raio da
base mede 6cm e a altura 8cm.
Solução: Para calcular a área total do
cone é preciso conhecer as medidas do
raio da base e da geratriz. Como foram
dados somente a medida do raio e da
altura, precisamos determinar a
medida da geratriz. Para isso
utilizaremos a relação fundamental
existente entre esses três elementos.
g 2 = h2 + r 2 Conhecidas as
g2 = 82 + 62 medidas do raio e da
g2 = 64 + 36 geratriz, basta aplicar
g2 = 100 a fórmula da área
g = 10 cm total. Segue que:

20. Exemplo 2. Determine a área total do cone
abaixo.
Solução: Pela figura temos
que r = 40 cm e g = 70 cm.
Como já conhecemos as
medidas do raio da base e
da geratriz, podemos
aplicar diretamente a
fórmula da área total.

21. Volume
Para determinar o volume do
cone, vamos ver como calcular
volumes de sólidos de revolução.
Observe a figura:

22. Sabemos, pelo Teorema de Pappus - Guldin, que,
quando uma superfície gira em torno de um eixo e,
gera um volume tal que: V = 2. .d.S
Vamos, então, determinar o volume do cone de
revolução gerado pela rotação de um triângulo
retângulo em torno do cateto h:
d = distância do
centro de gravidade
(CG) da sua
superfície ao eixo e
S=área da
superfície

23. O CG do triângulo está a uma
distância do eixo de rotação. Logo:

24. Fórmulas de áreas e volume:

25. DIVERSÃO
DE
CASA/AULA

26. 1 – Um cone circular reto tem 10 cm de raio da
base e 24 cm de altura. Calcule a área total e o
volume desse cone.
g2 = h2 + r2 AT = .r.(r + g)
g2 = 242 + 102 AT = .10.(10 + 26)
g2 = 676 AT = 360 cm2
g = 26 cm

27. 2 – A superfície lateral de um cone é um setor
circular de 12 cm e ângulo central de 120º. Calcule
a área total desse cone.
.122 _____ 360º
AL _____ 120º
AL = 144.
3
AL = 48 cm2
AL = .r.g AT = .r.(r + g)
48. = .r.12 AT = .4.(4 + 12)
r = 4 cm AT = 64 cm2

28. 3 – calcule a área total e o volume de um cone
equilátero cuja geratriz mede 20 cm. (Obs.: em um
cone equilátero, a geratriz é igual ao diâmetro da
base.)
g = 2.r g2 = h2 + r2 AT = .r.(r + g)
g = 20 cm 202 = h2 + 102 AT = .10.(10 + 20)
R = 10 cm h2 = 300 AT = 300 cm2
h = 10. 3 cm

29. 4 – Um cone é gerado pela rotação completa de um
triângulo retângulo, de catetos medindo 15 cm e 8
cm, em torno do cateto maior. Calcule a área total
e o volume desse cone.
g2 = h2 + r2 AT = .r.(r + g)
g2 = 152 + 82 AT = .8.(8 + 17)
g2 = 225 + 64 AT = 200 cm2
g2 = 289
g = 17 cm

30. 5 – Considere um triângulo retângulo de catetos
medindo 5 cm e 12 cm. Gira-se o triângulo em
torno do cateto maior, obtendo-se um cone
circular reto. Analise as proposições abaixo,
marcando (V) para as verdadeiras e (F) para as
falsas.
( V ) A geratriz do cone mede 13 cm.
( F ) A área lateral do cone é igual a 60 cm2.
( V ) O volume do cone é igual a 100 cm3.
( V ) A área total do cone é igual a 90 cm2.
( F ) O volume do cone obtido em torno do cateto
menor é o mesmo que daquele que se obtém em
torno do cateto maior.g

31. 6 – Um cone reto tem 4 cm de altura e o raio da
base mede 3 cm. Vamos calcular a área lateral e o
volume:
g2 = 42 + 32
g2 = 16 + 9 = 25 g = 5 cm
AL = .r.g
AL = .3.5
AL = 15 cm2
V=1.9 .4 V = 12 cm3
3

32. 7 – Vamos calcular o volume a área lateral de um
cone reto cuja geratriz é igual ao diâmetro da
base.
4r2 = h2 + r2
h2 = 3r2 h = r. 3
AB = .r2 V = .r2.r 3
h = r. 3 3
V = .r3 3
3
AL = .r.g
AL = .r.2r
AL = 2 r2 cm2

33. 8 – Calcule a área lateral e o volume de um cone
equilátero, sabendo que o raio da base mede 5 cm.
9 – Em um cone reto, o raio da base e a altura
medem respectivamente 5 cm e 12 cm. Determine:
a) Sua área lateral;
b) Sua área total;
c) Seu volume.
10 – Em um cone reto, a área lateral é igual a
48 cm2 e o raio da base mede 6 cm. Calcule a
geratriz.

34. 11 – Em um cone reto, o raio da base é a metade da
medida da geratriz e a área lateral 18 cm2 .
Calcule o raio da base e o volume do cone.
12 – A base de um cone reto está inscrita em um
quadrado de 6m de lado. Sabendo que a geratriz
do cone mede 5m, calcule o volume e a área lateral
do cone.
13 – Qual a geratriz de um cone equilátero cujo
volume é igual a . 3 cm3 ?

35. 14 – Qual o volume de
um cone circular reto
inscrito em um cilindro
de 4m de altura e raio
da base igual a 3m ?
15 – Qual o volume de
um cone reto inscrito
em um cubo de 3m de
aresta ?

36. 16 – Uma ampulheta é formada por dois cones
retos idênticos, tendo cada um deles 6 cm de
diâmetro na base e 10 cm de altura. Um deles está
completamente cheio de areia e esta ecoa para o
outro cone à razão de 0,5 cm3 por segundo.O
tempo necessário para escoar totalmente a areia
de um cone para outro é:
a) Menor que 2 min;
b) Entre 2min e 3 min;
c) Entre 3min e 4min;
d) Entre 4min e 5 min;
e) Maior que 5min.