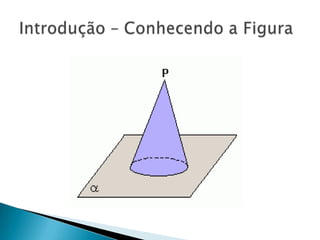
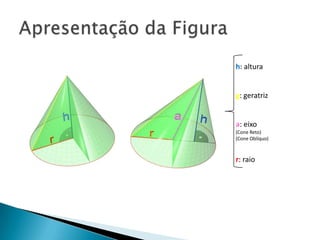
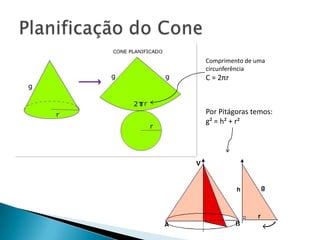
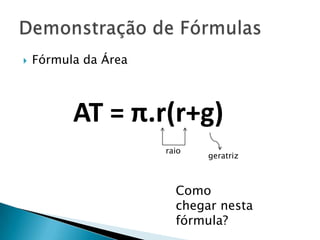
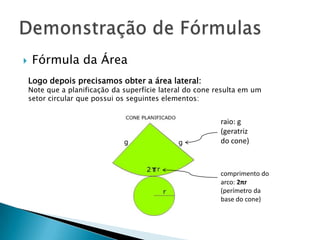
O documento apresenta fórmulas e exemplos relacionados a cones circulares retos. Inclui as fórmulas para calcular a área total, área da base e lateral, e volume de um cone, explicando os passos para chegar em cada uma. Também apresenta exemplos numéricos para ilustrar o uso das fórmulas.

1. Apresentação, planificação, demonstração de fórmulas e
exemplos
Daniel Oliveira
Danrley Moreira
João Robson
Matheus Marcelino
Samuel Ferreira
Tamires Nobre

4. 
Arquitetura
Catedral Metropolitana de São Sebastião do Rio de Janeiro

5. 
Trânsito

6. 
Natureza

7. 
Recuperação
Colar Elizabetano

8. 
Culinária

10. h: altura
g: geratriz
a: eixo
(Cone Reto)
(Cone Oblíquo)
r: raio

12. Comprimento de uma
circunferência
C = 2πr
Por Pitágoras temos:
g² = h² + r²

14. 
Fórmula da Área
AT = π.r(r+g)
raio
geratriz
Como
chegar nesta
fórmula?

15. 
Fórmula da Área
Devemos ter em mente que a área total é a soma da área da base e a área
da lateral.
AT = AL + AB

16. 
Fórmula da Área
Primeiro precisamos obter a área da base:
Como a base de um cone é uma circunferência, é dada pela
seguinte expressão:
Ab = π. r²
circ

17. 
Fórmula da Área
Logo depois precisamos obter a área lateral:
Note que a planificação da superfície lateral do cone resulta em um
setor circular que possui os seguintes elementos:
raio: g
(geratriz
do cone)
comprimento do
arco: 2πr
(perímetro da
base do cone)

18. 
Fórmula da Área
Para encontrarmos a área da superfície lateral, devemos
calcular a área do setor circular. Utilizando uma regra de três
simples:
Comprimento do arco
Área do setor
2πg
-----------πg²
2πr
-----------Alateral
2πg . Alateral = 2πr . πg²
Alateral = πrg

19. 
Fórmula da Área
Finalmente, para encontrarmos a área total de um
cone, basta somarmos a área lateral e a área do
circunferência:
Ab = πr²
área da
base
Al = πrg
At = Ab + Al
At = πr² + πrg
At = πr(g + r)
área
lateral

20. 
Fórmula do Volume
O volume do cone é dado pelo produto da área da base pela
altura divido por três.
Por que é dividido por
três (um terço) ?

22. 
Fórmula do Volume
Por que é um terço ?
Sabemos que a fórmula para encontrarmos o volume de um cilindro é
dada pela expressão:
V = πr²h
E a fórmula para encontrar o volume do cone é:
V = πr²h
3

23. 
Fórmula do Volume
Portanto, colocando as fórmulas lado a lado:
V = πr²h V = πr²h
3
Podemos afirmar que:
“O volume do cone é a terça parte do volume
do cilindro, de mesma base e de mesma
altura.”

24. 
Fórmula do Volume - Experiência
Se enchermos o cone com areia, será necessário despejar três vezes
seu conteúdo no interior do cilindro, para enchê-lo completamente.

25. 
Samuel
Ferreira
Fórmula do Volume
Logo, teremos a expressão do volume de um cone:
V = πr²h
3
π = 3,14
r = raio da
circunferência
h = altura do
cone

27. 
1) Calcule a área total de um cone de 8cm de
altura, sabendo que o raio da base mede 6cm.
h = 8cm
rbase = 6cm
g=?
At = ?
h
Por Pitágoras:
g² = h² + r²
g
8
6
r

28. 
1) Calcule a área total de um cone de 8cm de
altura, sabendo que o raio da base mede 6cm.
g² = h² + r²
g² = 8² + 6²
Utilizando a fórmula da área do cone:
g² = 64 + 36
AT = πr(r+g)
g² = 100
AT = 3,14.6.(6+10)
g = √ 100
AT = 18,84.16
g = 10
AT = 301,44 cm²

29. 
2) Deseja-se construir um cone circular reto, utilizando para isso papel.
Sabendo que o cone deve apresentar 20 cm de altura e que a geratriz terá 25
cm de comprimento, quantos centímetros quadrados de papel serão gastos
para confeccionar esse cone? (Use π= 3,14).
h = 20cm
g = 25cm
r=?
At = ?
h
25
20
Por Pitágoras:
g² = h² + r²
g
r