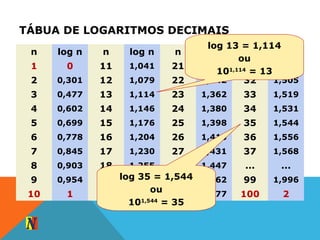
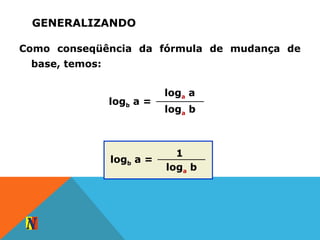
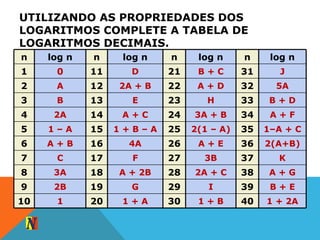
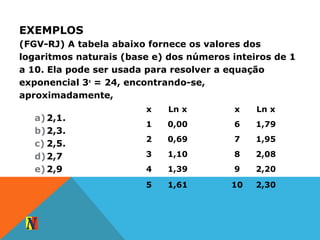
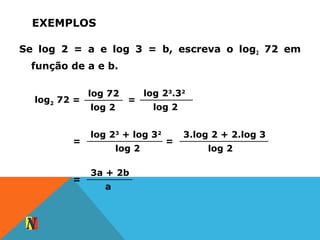
O documento apresenta exemplos de cálculos envolvendo logaritmos decimais e neperianos. Inicialmente, explica como Giovanna calculou o tempo necessário para que seu dinheiro aplicado a juros compostos atingisse o valor desejado para comprar um computador. Posteriormente, discute a história dos logaritmos e suas aplicações em equações exponenciais e potenciações.

1. LOGARITMOS

2. QUAL É O TEMPO?
Giovanna ganhou 1 000 reais de seu pai pra fazer
sua festa de 15 anos. Ao receber o dinheiro, no
entanto, resolveu abri mão da festa. É que ela
queria comprar um computador.
Mas havia um problema: o computador que ela
queria custava 1 500 reais. O jeito era aplicar o
dinheiro que tinha, até conseguir o valor
necessário.

3. QUAL É O TEMPO?
Giovanna foi ao banco e conseguiu uma taxa de 5
% ao mês, capitalizados mensalmente.
Chegando em casa, ficou curiosa. Em quanto
tempo os 1000 reais aplicados se transfor-
mariam nos 1500 reais de que precisava?
Ela havia acabado de aprender a calcular juros
compostos. Fez, então, as suas contas.

4. VEJA OS CÁLCULOS
Capital aplicado: C = 1 000
Taxa: 5 % ao mês = 0,05 ao mês
Montante pretendido: M = 1 500,00
M = C.(1 + i)t ⇒ 1 500 = 1 000 . (1,05)t
⇒ 1,05t
= 1,5
Giovanna concluiu, portanto, que seu objetivo seria
atingido no final do 9º mês de aplicação.
1,057
≈ 1,407
1,058
≈ 1,477
1,059
≈ 1,551

5. QUAL É O EXPOENTE?
Como poderia ser obtido, com uma aproximação
razoável e sem utilizar o método das tentativas,
o valor de t na equação 1,05t
= 1,6?
A teoria dos logaritmos é muito útil em problemas
como esse, que envolve a determinação de um
expoente.

6. HISTÓRIA
A invenção dos logaritmos ocorreu no início do
século XVII e é creditada ao escocês John
Napier e ao suiço Jobst Burgi.
Inicialmente seu objetivo era simplificar os
cálculos numéricos, principalmente em
problemas ligados à Astronomia e à Navegação.
A partir dessa fabulosa invenção, tornaram-se
mais simples e mais ágeis cálculos de
expressões como

7. HISTÓRIA
A partir dessa fabulosa invenção, tornaram-se
mais simples e mais ágeis cálculos de
expressões como
2,382,5
5,13,8
. √12,43
O valor dessa expressão equivale ao valor de
102,5.log 2,38 + (1/3).log 12,4 – 3,8.log 5,1

8. HISTÓRIA
Foi o matemático inglês Henry Briggs (1561 –
1631) quem propôs, inicialmente, a utilização do
sistema de logaritmos decimais. Afinal, o nosso
sistema de numeração utiliza justamente a base
10.

9. HISTÓRIA
Atualmente, são inúmeras as aplicações
tecnológicas dos logaritmos. Eles são úteis, por
exemplo, na resolução de problemas que
envolvem desintegração radiotiva, o
crescimento de uma população de animais ou
bactérias, etc.

10. TRABALHANDO COM
POTÊNCIAS DE BASE
10

11. A BASE 10
Todo número positivo pode ser escrito como uma
potência de base 10, ou como uma aproximação
dessa potência. Veja os exemplos:
1 = 100
0,1 = 10–1
10 = 101
0,01 = 10–2
100 = 102
0,001 = 10–3
1 000 = 103
0,0001 = 10–4
10 000 = 104
0,00001 = 10–5

12. A BASE 10
2 = 100,301
3 = 100,477
7 = 100,845
11 = 101,041
13 = 101,114
Na maioria dos casos, torna-se difícil escrever um
número como potência de base 10. Em valores
aproximados apresentamos os exemplos:

13. EXEMPLOS
Usando as igualdades 2 = 100,301
e 3 = 100,477
, escreva
os números 4, 5 e 6 como potência de base 10.
 4 = 22
= (100,301
)2
= 100,602
 5 = = = 101 – 0,301
10
2
10
100,301
= 100,699
 6 = 2.3 = 100,301
. 100,477 = 100,301 + 0,477
= 100,778

14. EXEMPLOS
Usando as igualdades 2 = 100,301
e 3 = 100,477
, escreva
o número 60 como potência de base 10.
 60 = 2.3.10 = 100,301
. 100,477
. 10
⇒ 60 = 100,301 + 0,477 + 1
⇒ 60 = 101,778

15. EXEMPLOS
Usando as igualdades 2 = 100,301
e 3 = 100,477
, resolva
a equação exponencial 2x
= 12.
2x
= 12 ⇒ 2x
= 22
.3
⇒ (100,301
)x
= (100,301
)2
. 100,477
⇒ 100,301.x
= 100,602
. 100,477
⇒ 100,301.x
= 101,079 ⇒ 0,301.x = 1,079
⇒ x =
1,079
0,301
⇒ x ≈ 3,585

16. LOGARITMO
COMO
EXPOENTE

17. LOGARITMO COMO EXPOENTE
O conceito de logaritmo está associado à operação
potenciação: mais precisamente à determinação
do expoente. Veja:
2x
= 8 ⇒ x = 3
No caso, dizemos, que o logaritmo de 8, na base 2 ,
é igual ao expoente 3. Em símbolos,
log2 8 = 3

18. LOGARITMO COMO EXPOENTE
Observe: calcular o log2 8 é descobrir o expoente
ao qual se deve elevar a base 2, para obter,
como resultado, a potência 8.
Vale, portanto a equivalência:
log2 8 = 3 ⇔ 23
= 8
Calcular um logaritmo é obter um expoente.
Logaritmo é o mesmo que expoente.

19. DEFINIÇÃO
Suponhamos dois reais positivos a e b (a ≠ 1). Se
ax
= b, dizemos que x é o logaritmo de b na base
a (simbolicamente loga b = x).
loga b = x ⇔ ax
= b
 a é a
base; b é o logaritmando ou antilogaritmo;
 x é o logaritmo;

20. EXEMPLOS
 log5 √25 = 2/3, porque 52/3
= √252
 log2 32 = 5, porque 25
= 32
 log3 (1/81) = –4, porque 3–4
= 81
 log10 0,001 = –3, porque 10–3
= 0,001
3 3
De acordo com a definição, calcular um logaritmo
é descobrir o expoente, ou seja, resolver uma
equação exponencial.

21. EXEMPLOS
 Calcular log4 8.
log4 8 = x ⇒ 4x
= 8 ⇒ (22
)x
= 23
⇒ 22x
= 23 ⇒ x = 3

22. EXEMPLOS
 Calcular log1/3 √9.5
log1/3 √9 = x5
⇒
1
3
x
= √95
⇒ (3–1
)x
= 32/5 ⇒ 3–x
= 32/5
⇒ –x = 2/5
⇒ x = –2/5

23. CONDIÇÃO DE EXISTÊNCIA DO
LOGARITMO
Da definição, concluímos que o logaritmo só existe
sob certas condições:
loga b = x ⇔
b > 0
a > 0
a ≠ 1

24. CONDIÇÃO DE EXISTÊNCIA
 Analise quais seriam os significados de log2 (–4),
log(–2) 8, log7 0, log1 6 e log0 2, caso fossem
definidos.
log2 (–4) = x ⇒ 2x
= –4 impossível
log–2 8 = x ⇒ (–2)x
= 8 impossível
log7 0 = x ⇒ 7x
= 0 impossível
log1 6 = x ⇒ 1x
= 6 impossível
log0 2 = x ⇒ 0x
= 2 impossível

25. OBSERVAÇÃO
Muitas vezes, um logaritmo envolve variáveis.
Nesse caso, devemos analisar o domínio dessas
variáveis. Para isso, usamos as condições de
existência do logaritmo.

26. EXEMPLOS
 Resolver a equação logx (2x + 8) = 2.
1o
. Vamos analisar a condição de existência do logaritmo.
2x + 8 > 0
x > 0
x ≠ 1
⇒
x > –4
x > 0
x ≠ 1
⇒
x > 0
x ≠ 1
2o
. Usando a definição de logaritmo.
logx (2x + 8) = 2 ⇒ x2
= 2x + 8 ⇒ x2
– 2x – 8 = 0
⇒ x = –2 ou x = 4. ⇒ S = {4}

27. CONSEQÜÊNCIA
S DA
DEFINIÇÃO

28. CONSEQÜÊNCIAS DA DEFINIÇÃO
Admitindo-se válidas as condições de existência
dos logaritmos, temos os seguintes casos
especiais, que são conseqüências da definição.
loga 1 = 0
loga a = 1
loga ak
= k
porque a0
= 1
porque a1
= a
porque ak
= ak

29. EXEMPLOS
 log3 3 = log10 10 = log3,7 3,7 = 1
 log3 1 = log10 1 = log3,7 1 = 0
 log3 39
= 9
 log10 10–3
= –3

30. CONSEQÜÊNCIAS DA DEFINIÇÃO
Sabemos que loga k é o expoente ao qual se deve
elevar a base a para se obter k. Vale por isso, a
seguinte igualdade:
loga k
a = k

31. EXEMPLOS
log5 3
 5 = 3
1 + log2 6
 2 = 21
.2
log2 6
= 2.6 = 12
log3 5
 9 = (32
)
log3 5
3
log3 5 2
= = 52
= 25
1 – log15 3
 15 = log15 3
151
15
=
15
3
= 5

32. SISTEMA DE
LOGARITMOS

33. SISTEMA DE LOGARITMOS
Sistema de logaritmos é o conjunto de todos os
logaritmos numa determinada base. Entre os
infinitos sistema de logaritmos, destacam-se dois:
O sistema de logaritmos decimais utiliza a base 10.
No cálculo de logaritmos decimais, convenciona-se
não escrever a base, ou seja, log x é o mesmo que
log10 x.
log x logaritmo decimal de x (→ base 10)

34. EXEMPLOS
 log 1000 = log10 1000 = 3
 log 0,01 = log10 10–2
= –2
 log 1 = log10 1 = 0
 log 100 = log10 100 = 2

35. SISTEMA DE LOGARITMOS
O sistema de logaritmos naturais ou neperianos,
utiliza, como base, o número irracional e.
Esse número foi introduzido por Euler, em meados do
século XVIII. Seu valor aproximado é e =
2,71828.
O logaritmo natural de um número x pode ser
indicado por Ln x.
Ln x logaritmo natural de x (→ base e)

36. EXEMPLOS
 Ln e = loge e = 1
 Ln 10 = loge 10 ≈ 2,3
 Ln e3
= loge e3
= 3

37. OBSERVAÇÃO
Chama-se co-logaritmo de a na base b (em
símbolos, cologb a) o oposto do logaritmo de a
na base b.
cologb a = – logb a
 colog2 8 = – log2 8 = –3
 colog3 (1/9) = – log3 (1/9) = 2

38. LOGARITMOS
DECIMAIS

39. LOGARITMOS DECIMAIS
O primeiro a utilizar os logaritmos decimais foi o
matemático inglês Henry Briggs (1561-1631).
Foi ele quem construiu a primeira tábua de
logaritmos decimais.

40. TÁBUA DE LOGARITMOS DECIMAIS
n log n n log n n log n n log n
1 0 11 1,041 21 1,322 31 1,491
2 0,301 12 1,079 22 1,342 32 1,505
3 0,477 13 1,114 23 1,362 33 1,519
4 0,602 14 1,146 24 1,380 34 1,531
5 0,699 15 1,176 25 1,398 35 1,544
6 0,778 16 1,204 26 1,415 36 1,556
7 0,845 17 1,230 27 1,431 37 1,568
8 0,903 18 1,255 28 1,447 ... ...
9 0,954 19 1,279 29 1,462 99 1,996
10 1 20 1,301 30 1,477 100 2
log 13 = 1,114
ou
101,114
= 13
log 35 = 1,544
ou
101,544
= 35

41. EXEMPLOS
 Calcule os logaritmos decimais
a) log 10
b) log 10 000
c) log 1013
d) log 10–30
e) log 0,000001

42. EXEMPLOS
 Consultando a tábua de logaritmos calcule
a) log 60 + log 31 – log 5
b) 100,903
+ 101,505
– 1000,69
c) os valores de x e y tais que 10x
= 26 e
1000y
= 15

43. EXEMPLOS
 Em valores aproximados, a tábua de logaritmos
mostra que log 13 = 1,114 ou 101,114
= 13. A partir
desses valores, sem uso de calculadora, obtenha
os números seguintes.
a) 102,114
; 104,114
; 100,114
e 1001,557
.
b) log 130; log 13000; log 1,3 e log 1300
c) os valores de x e y tais que 10x
= 0,13 e
13y
= 103,342
.

44. MUDANÇA DE
BASE

45. MUDANÇA DE BASE
Observe uma calculadora científica. Ela permite o
cálculo apenas dos logaritmos decimais (tecla
log) e dos logaritmos naturais (tecla Ln).
Como obter então, numa calculadora, logaritmos
em outras bases?
Será possível achar, por exemplo, os valores de
log3 5 e log7 23?

46. MUDANÇA DE BASE
Na tábua de logaritmos decimais, encontramos
que log10 23 = 1,362 e log10 7 = 0,845. A partir
deles, determine o valor log7 23.
log10 23 = 1,362 ⇒ 101,362
= 23
log10 7 = 0,845 ⇒ 100,845
= 7
log7 23 = x ⇒ 7x
= 23
⇒ (100,845
)x
= 101,362
⇒ 100,845.x
= 101,362
⇒ 0,845.x = 1,362
1,362
0,845
⇒ x = = 1,612
log7 23 =
log10 23
log10 7

47. FÓRMULA DE MUDANÇA DE BASE
De modo geral, podemos calcular logba, utilizando
uma outra base k arbitrária. Para isso, dividimos
o logaritmo de a pelo logaritmo de b, na base k
escolhida.
logk a
logk b
Logb a =

48. EXEMPLOS
 Pela tecla Ln (logaritmo natural) de uma
calculadora, obtemos Ln 6 = 1,792 e Ln 2 = 0,693.
A partir desses valores, calcular log2 6.
loge 6
loge 2
log2 6 =
Ln 6
Ln 2
=
1,792
0,693
= = 2,586

49. EXEMPLOS
 Resolver a equação 5x
= 20, dados os logaritmos
decimais log 5 = 0,699 e log 20 = 1,301.
5x
= 20 ⇒ x = log5 20
log10 20
log10 5
log5 20 =
log 20
log 5
=
1,301
0,699
= = 1,861

50. EXEMPLOS
 Se logk x = 2, calcular logx (1/k).
logk (1/k)
logk x
logx (1/k) =
–1
2
=

51. EXEMPLOS
 Se log 2 = 0,30 e log 3 = 0,48, calcular log2 3.
log 3
log 2
log2 3 =
0,48
0,30
=
1o
. Vamos a fórmula de mudança de base.
= 1,6
Observe que, log2 3 = 1,6 ⇔ 21,6
= 3.

52. EXEMPLOS
 Escrevendo os logaritmos numa mesma base,
obtenha o valor mais simples do produto
log2 7 . Log7 13 . Log13 2
log 7
log 2
.
1o
. Vamos a fórmula de mudança de base.
log 13
log 7
. log 2
log 13
= 1
1
1
1
1
1
1

53. CONSEQÜÊNCIA – MUDANÇA DE BASE
 Compare os valores dos log5 25 e log25 5.
 Compare, também, os valores log2 8 e log8 2.
 Que conclusão se pode tirar dessas comparações?
 Se logx y = 3/5, calcule logy x.
log5 25 = 2 e log25 5 = 1/2
log2 8 = 3 e log8 2 = 1/3
logb a = 1/loga b
logy x = 5/3

54. GENERALIZANDO
Como conseqüência da fórmula de mudança de
base, temos:
loga a
loga b
logb a =
1
loga b
logb a =

55. PROPRIEDADE
S DOS
LOGARITMOS

56. PROPRIEDADES DOS LOGARITMOS
O logaritmo tem uma particularidade importante. Ele
transforma operações mais complicadas em
operações mais simples.
Com as propriedades dos logaritmos podemos
transformar:
 multiplicações em adições;
 divisões em subtrações;
 potenciações em multiplicações;
 radiciações em divisões.

57. LOGARITMO DO PRODUTO
Vamos calcular o valor do log 21, a partir dos
valores de log 3 = 0,477 e log 7 = 0,845.
log 3 = 0,477 ⇒ 100,477
= 3
log 7 = 0,845 ⇒ 100,845
= 7
log 21 = x ⇒ 10x
= 21
⇒ 10x
= 3.7 ⇒ 10x
= 100,477
.100,845
⇒ x = 0,477 + 0,845 ⇒ x = 1,322
⇒ 10x
= 100,477 + 0,845
log 21 = log (3.7) = log 3 + log 7

58. LOGARITMO DO PRODUTO
De modo geral, o logaritmo do produto de dois
números, numa certa base, é a soma dos
logaritmos desses números, na mesma base.
Loga (x.y) = loga x + loga y
Para o produto de três ou mais fatores, a propriedade
continua válida.

59. EXEMPLOS
A partir de log 2 = 0,301 e log 13 = 1,114, calcular log 26 e log 2000.
 log 26 = log (2.13) = log 2 + log 13
log 26 = 0,301 + 1,114 = 1,415
 log 2000 = log (2.1000) = log 2 + log 1000
log 2000 = 0,301 + 3 = 3,301

60. EXEMPLOS
Sendo x e y reais positivos, decompor log3 (9xy)
numa soma de logaritmos.
log3 (9xy) = log3 9 + log3 x + log3 y
log3 (9xy) = 2 + log3 x + log3 y

61. EXEMPLOS
Transformar num único logaritmo e calcular o
valor da expressão log 4 + log 5 + log 50.
log 4 + log 5 + log 50 = log (4.5.50)
log 4 + log 5 + log 50 = log 1000 = 3

62. LOGARITMO DO QUOCIENTE
Vamos calcular o valor do log (3/2), a partir dos
valores de log 2 = 0,301 e log 3 = 0,477.
log 2 = 0,301 ⇒ 100,301
= 2
log 3 = 0,477 ⇒ 100,477
= 3
log (3/2) = x ⇒ 10x
= 3/2
⇒ 10x
=
3
2
=
100,477
100,301
= 100,477 – 0,301
⇒ x = 0,477 – 0,301 ⇒ x = 0,176
log (3/2) = log 3 – log 2

63. LOGARITMO DO QUOCIENTE
De modo geral, o logaritmo do quociente de dois
números, numa certa base, é a diferença dos
logaritmos desses números, na mesma base.
Loga = loga x – loga yx
y

64. EXEMPLOS
A partir de log 2 = 0,301 obter log 5.
log 5 = log
10
2
= log 10 – log 2 = 1 – 0,301
⇒ log 5 = 0,699

65. EXEMPLOS
Se x e y são reais positivos, decompor em parcelas
log2 (x/4y).
log2
x
4y
= log2 x – log2 4y
= log2 x – (log2 4 + log2 y)
= log2 x – (2 + log2 y)
= log2 x – 2 – log2 y
= log2 x – log2 y – 2

66. EXEMPLOS
Compor (transformar num único logaritmo) a
expressão E = log m – log 3 + 2 – log n.
1º. Vamos transformar a parcela 2 na forma de logaritmo
decimal. log 100 = 2.
E = log m – log 3 + log 100 – log n
E = (log m + log 100) – (log 3 + log n)
E = (log 100m) – (log 3n)
E = log
100m
3n

67. LOGARITMO DA POTÊNCIA
Vamos calcular o valor do log 34
, a partir do valor
de log 3 = 0,477.
log 3 = 0,477 ⇒ 100,477
= 3
log 34
= x ⇒ 10x
= 34
⇒ 10x
= (100,477
)4
⇒ x = 4 . 0,477 ⇒ x = 1,908
log 34
= 4 . log 3

68. LOGARITMO DA POTÊNCIA
Generalizando, o logaritmo de uma potência, é
igual ao produto do expoente da potência pelo
logaritmo da base.
Loga xk
= k . loga x

69. EXEMPLOS
A partir do log 3 = 0,477, calcular log 0,009.
log 0,009 = log
9
100
= log 9 – log 100
= log 32
– 2 = 2 . log 3 – 2
= 2 . 0,477 – 2
= 0,954 – 2 = – 1,046

70. EXEMPLOS
Calcular log , a partir dos valores log 2 =
0,301, log 3 = 0,477 e log 13 = 1,114.
13√3
4
log
13√3
4
= log 13 + log √3 – log 4
= log 13 + log 31/2
– log 22
= log 13 + . log 3 – 2 . log 21
2
= 1,144 + 0,5.0,477 – 2.0,301
= 1,144 + 0,2385 – 0,601 = 0,7505

71. EXEMPLOS
Compor e simplificar a expressão
E = 2.log3 12 – log3 8 – 2
1
3
1º. Vamos transformar a parcela 2 na forma de logaritmo
de base 3. (log3 9 = 2).
E = 2.log3 12 – log3 8 + log3 9
1
3
E = log3 122
– log3 81/3
+ log3 9
E = log3 144 – log3 2 + log3 9 = log3 144 – log3 (2.9)
E = log3 144 – log3 18 ⇒ E = log3
144
18
= log3 8

72. UTILIZANDO AS PROPRIEDADES DOS
LOGARITMOS COMPLETE A TABELA DE
LOGARITMOS DECIMAIS.
1 + 2A401 + B301 + A20110
B + E39I29G192B9
A + G382A + C28A + 2B183A8
K373B27F17C7
2(A+B)36A + E264A16A + B6
1–A + C352(1 – A)251 + B – A151 – A5
A + F343A + B24A + C142A4
B + D33H23E13B3
5A32A + D222A + B12A2
J31B + C21D1101
log nnlog nnlog nnlog nn

73. EXEMPLOS
(FGV-RJ) A tabela abaixo fornece os valores dos
logaritmos naturais (base e) dos números inteiros de 1
a 10. Ela pode ser usada para resolver a equação
exponencial 3x
= 24, encontrando-se,
aproximadamente,
x Ln x x Ln x
1 0,00 6 1,79
2 0,69 7 1,95
3 1,10 8 2,08
4 1,39 9 2,20
5 1,61 10 2,30
a)2,1.
b)2,3.
c) 2,5.
d)2,7
e)2,9

74. EXEMPLOS
Se log 2 = a e log 3 = b, escreva o log2 72 em
função de a e b.
log2 72 =
log 72
log 2
=
log 23
.32
log 2
=
log 23
+ log 32
log 2
=
3.log 2 + 2.log 3
log 2
=
3a + 2b
a