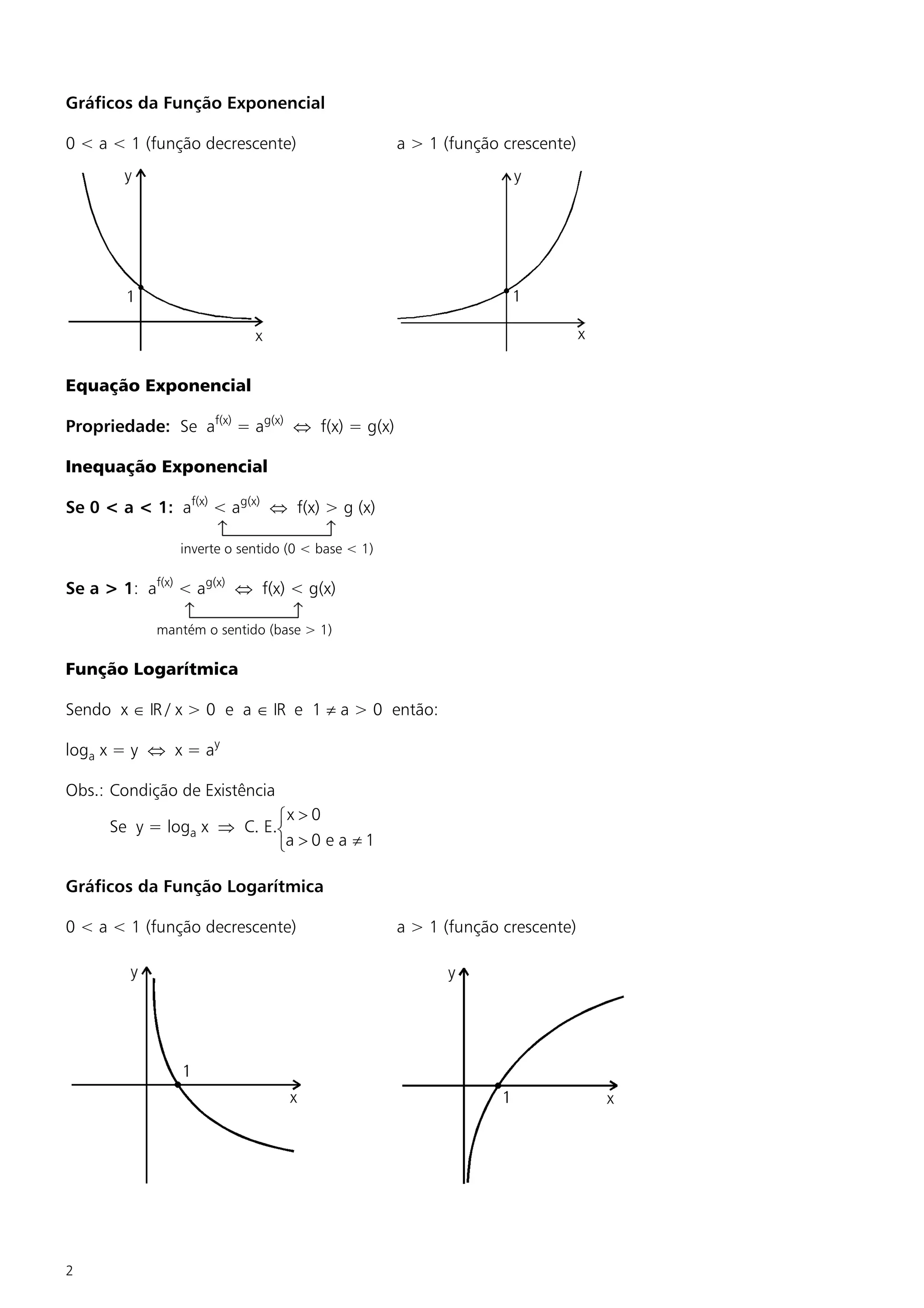
1) O documento apresenta um resumo teórico sobre funções exponenciais e logaritmos, incluindo propriedades das potências, funções exponenciais, gráficos, equações e inequações exponenciais e logaritmos. 2) São fornecidos exercícios sobre o assunto com dicas de resolução. 3) As resoluções dos exercícios aplicam as propriedades apresentadas no resumo teórico.

1. Matemática
Fascículo 01
Álvaro Zimmermann Aranha

2. Índice
Função Exponencial e Logaritmos
Resumo Teórico ..................................................................................................................................1
Exercícios............................................................................................................................................4
Dicas ..................................................................................................................................................5
Resoluções .........................................................................................................................................6

3. Função Exponencial e Logaritmos
Resumo Teórico
Potência
Sendo a Î IR e n Î IN , temos:
ìa 0 = 1
Def.: í n+ 1
îa = an × a
Consequência: a n = a ×4× a 4 a
1a 2 K 3
n vezes
Propriedades das Potências
P1: a m × a n = a m+ n
am
P2: = am - n
n
a
P3: (a m ) n = a m × n
P4: (a × b)m = am × bm
m
æaö am
P5: ç ÷ =
è bø bm
1
Obs. 1: a -n = (a ¹ 0)
an
n m
Obs. 2: am = a n (n Î IN* e am ³ 0)
Função Exponencial
É toda função da forma y = ax com a Î IR , a > 0 e a ¹ 1.
1

4. Gráficos da Função Exponencial
0 < a < 1 (função decrescente) a > 1 (função crescente)
Equação Exponencial
Propriedade: Se af(x) = ag(x) Û f(x) = g(x)
Inequação Exponencial
Se 0 < a < 1: af(x) < ag(x) Û f(x) > g (x)
inverte o sentido (0 < base < 1)
Se a > 1: af(x) < ag(x) Û f(x) < g(x)
mantém o sentido (base > 1)
Função Logarítmica
Sendo x Î IR / x > 0 e a Î IR e 1 ¹ a > 0 então:
loga x = y Û x = ay
Obs.: Condição de Existência
ìx > 0
Se y = loga x Þ C. E.í
îa > 0 e a ¹ 1
Gráficos da Função Logarítmica
0 < a < 1 (função decrescente) a > 1 (função crescente)
2

5. Propriedade dos logaritmos
P1: loga (b . c) = loga b + loga c
b
P2: loga æ ö = loga b – loga c
ç ÷
èc ø
P3: loga bn = n loga b
1
P4: logan b = loga b
n
logc a
Fórmula de mudança de base: logb a =
logc b
Equação Logarítmica
1.o Tipo: loga f(x) = loga g(x) Û f(x) = g(x)
2.o Tipo: loga f(x) = a Û f(x) = aa (a Î IR)
Obs.: Ao resolver as equações logarítmicas, é necessário verificar as condições de existência da
equação inicial.
Inequação Logarítmica
1.o Tipo: log < log
Se 0 < a < 1
loga f(x) < loga g(x) Û f(x) > g(x)
inverte o sentido (0 < base < 1)
Se a > 1
loga f(x) < loga g(x) Û f(x) < g(x)
mantém o sentido (base > 1)
2.o Tipo: log < a (a Î IR)
Se 0 < a < 1
loga f(x) < a Û f(x) > aa
inverte o sentido (0 < base < 1)
Se a > 1
loga f(x) < a Û f(x) < aa
mantém o sentido (base > 1)
Obs.: Ao resolver as inequações logarítmicas, é necessário verificar as condições de existência da
inequação inicial.
3

6. Exercícios
01. A figura ao lado mostra o gráfico da função logaritmo na base b.
O valor de b é:
1
a.
4
b. 2
c. 3
d. 4
e. 10
02. O número x > 1 tal que logx2 = log4x é:
2 2 2
a. b. 2 c. 2 d. 2 2 e. 4
4
03. O número real x que satisfaz a equação log2 (12 – 2x) = 2x é
a. log25 b. log2 3 c. 2 d. log2 5 e. log23
04. Em que base o logaritmo de um número natural n, n > 1, coincide com o próprio número n?
1 1
a. nn b. c. n2 d. n e. n n
n
05. Considere a função f, definida por f(x)= logax. Se f(a) = b e f(a+2) = b + 1, os valores respectivos de
a e b são:
a. 2 e 1 b. 2 e 2 c. 3 e 1 d. 3 e 2 e. 4 e 1
06. O mais amplo domínio real da função dada por f(x) = log3 (2x - 1) é
1
a. ì x Î IR | x ¹ ü
í ý
î 2þ
1
b. ì x Î IR | x > ü
í ý
î 2þ
1
c. ì x Î IR | < x £ 1ü
í ý
î 2 þ
d. { x Î IR | x ³ 1}
e. { x Î IR | x ¹ 1}
ì x + y = 2y
ï
07. Se o par ordenado (a; b) é a solução do sistema í 2 , então a × b é igual a
ïlog10 (3x + 4) = 1 + log10 (y - 1)
î
a. 2 b. 4 c. 6 d. 8 e. 9
4

7. Dicas
01. Observando o gráfico, vemos que para x = 0,25 temos y = –1. Substituindo x e y em y = logbx,
obtemos b.
02. Resolver a equação na base 2, utilizando a propriedade de mudança de base:
logc a
logab = (b > 0, a > 0 e a ¹ 1, c > 0 e c ¹ 1)
logc b
03. Devemos ter 12 – 2x > 0 (condição de existência). Para resolver a equação, use a definição de
logaritmo (logab = c Û b = ac ) e substitua 2x por y.
04. É dado no enunciado que logxn = n (0 < x ¹ 1 e n > 1). Para obter a base x, aplique a definição de
logaritmo.
05. Como f(x) = loga(x), f(a) = b e f(a + 2) = b + 1, trocando-se x por a e por a + 2, obtemos os valores
de a e b.
06.
1. Para determinar o domínio de f(x) = log3 (2x - 1) ,devemos ter log3(2x – 1) ³ 0.
2. Para resolver a inequação logarítmica, basta notarmos que são equivalentes as inequações:
logaf(x) ³ c Û logaf(x) ³ c × logaa Û
Û logaf(x) ³ logaac Û f(x) ³ ac se a > 1 e c Î IR
07.
1. Obtenha uma relação entre x e y na 1.a equação do sistema, lembrando que
a n = n a m (a Î IR * , m Î Z e n Î IN*) e ab = ac Û
m
+
b = c (0 < a ¹ 1).
2. Na 2.a equação do sistema, use a propriedade do logaritmo do produto:
loga(b × c) = logab + logac e a consequência da definição:
logab = logac Û b = c (0 < a ¹ 1, b > 0 e c > 0).
3. Resolva o sistema obtido, equivalente ao sistema dado.
5

8. Resoluções
01. Alternativa d.
Do gráfico, temos: x = 0,25 e y = – 1.
1 –1 1
Sendo y = logbx, vem: – 1 = logb0,25 Þ – 1 = logb Þb = Þb=4
4 4
02. Alternativa b.
logx2 = log4x
Aplicando a propriedade de mudança de base:
logc b log2 2 log2 x
logab = (b > 0, a > 0 e a ¹ 1, c > 0 e c ¹ 1) temos: =
logc a log2 x log2 4
1 log2 x
Como log22 = 1 e log24 = 2 vem: =
log2 x 2
(log2 x) 2 = 2
ìlog2 x = 2
ï
log2 x = ± 2 Þ íou
ïlog2 x = - 2(não serve pois x > 1)
î
2
De log2x = 2 obtemos, pela definição de logaritmo, que x = 2
03. Alternativa e.
Devemos ter 12 – > 0 (condição de existência)
log (12 – 2x) = 2x Û 22x = 12 – 2x Û 22x + 2x – 12 = 0 Û
2
Û (2x)2 + 2x – 12 = 0
Seja 2x = y
y2 + y – 12 = 0
-1 ± 7
y= Þ y = – 4 ou y = 3
2
Se y = – 4 temos que 2x = – 4 (não convém, pois 2x > 0 para todo x real)
Se y = 3 temos que 2x = 3, que satisfaz a condição 12 – 2x > 0.
Sendo 2x = 3, conclui-se que x = log23
04. Alternativa e.
Seja x a base procurada. É dado no enunciado que:
logxn = n para 0 < x ¹ 1 e n > 1
1 1 1
Assim, logxn = n Û x n = n Û (x n ) n = (n) n Û x = n n
6

9. 05. Alternativa a.
f(x) = loga(x)
ì0 < a ¹ 1
ï
condições de existência íe
ïx > 0
î
Se f(a) = b, temos que loga(a) = bb = 1
Se f(a + 2) = b + 1, temos que loga(a + 2) = 2a2 = a + 2
1± 3
a2 – a – 2 = 0 Þ a = Þ a = 2, a = – 1 (não serve)
2
Resposta: a = 2 e b = 1
06. Alternativa d.
f(x) = log3 (2x - 1)
Para que exista f(x) Î IR, devemos ter:
log3(2x – 1) ³ 0
log3(2x – 1) ³ 0 × log33 Þ log3(2x – 1) ³ log33º
log3(2x – 1) ³ log31 Þ 2x – 1 ³ 1 Þ 2x ³ 2 Þ x ³ 1
Então: D(f) = { x Î IR | x ³ 1}
07. Alternativa b.
ì 2 x+y = 2 y
ï 
í
ïlog10 (3x + 4) = log10 10 + log10 (y – 1) ‚
î
x+ y
x+y
 2 2 = 2y Û = y Û x + y = 2y Û x = y
2
‚ log10(3x + 4) = log1010(y – 1) Û 3x + 4 = 10(y – 1) Û
Û 3x + 4 = 10y – 10 Û 3x = 10y – 14
condição de existência: 10(y – 1) > 0 Þ y > 1
ìx = y
Assim, o sistema dado é equivalente a: í
î3x = 10y - 14
3x = 10x – 14 Þ – 7x = – 14 Þ x = 2
Como x = y temos que y = 2 (satisfaz a condição y > 1)
Logo, a solução do sistema (a; b) é (2; 2)
Então: a × b = 2 × 2 = 4
7