O documento discute noções básicas de probabilidade, incluindo: 1) Definição de espaço amostral e evento; 2) Definição formal de probabilidade como a razão entre o número de elementos do evento e o número total de elementos do espaço amostral; 3) Exemplos de cálculo de probabilidades para lançamento de dados, sorteios numéricos e retirada de bolas de urnas.

1. NOÇÕES DE PROBABILIDADE
1. Espaço Amostral e Evento
Espaço Amostral (E) é o conjunto de todos os resultados
possíveis de um dado experimento.
Exemplo: No lançamento de um dado, o espaço amostral é:
E = {1, 2, 3, 4, 5, 6} seis possíveis (lados do dado).
No lançamento de uma moeda, o espaço amostral é:
E = {1, 2} dois possíveis (cara e coroa).
Evento (A) é qualquer subconjunto de um espaço amostral.
Exemplo: No lançamento de um dado, o evento
A = {2} é um evento considerando os seis possíveis
números (1, 2, 3, 4, 5, 6).
A = {2} é um evento considerando a possível
ocorrência de um número par (2, 4, 6).

2. 2. Definição
Probabilidade é o quociente entre o número de elementos do evento desejado
[n(A)] e o número de elementos do espaço amostral [n(E)], desde que as
amostras desse espaço amostral possam ocorrer de maneira eqüiprováveis
(mesmas chances de ocorrer).
)(
)(
)(
En
An
AP
1)(0 AP
n(A) é o número de elementos
do evento desejado
n(E) é o número de elementos
do espaço amostral
Exemplo:
Num sorteio com número de 1 a 30, a
probabilidade de ser sorteado um número múltiplo
de 5 é:
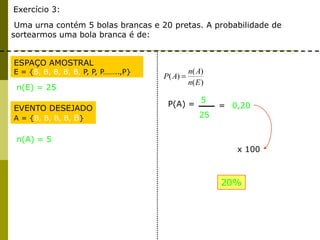
ESPAÇO AMOSTRAL
E = {1, 2, 3, ….., 23, 24, 30}
n(E) = 30
EVENTO DESEJADO
A = {5, 10, 15, 20, 25, 30}
n(A) = 6
)(
)(
)(
En
An
AP =
6
30
=0,20 ou 20%

3. Exercício 1:
Joga-se um dado “honesto” de seis faces e lê-se o número da face
voltada para cima. Calcular a probabilidade de se obter:
ESPAÇO AMOSTRAL
E = {1, 2, 3, 4, 5, 6}
a) EVENTO DESEJADO
A = {3 }
n(A) = 1
n(E) = 6
)(
)(
)(
En
An
AP
P(A) =
1
6
= 0,16667..
a) o número 3
b) um número par
c) um número maior que 2
d) um número menor que 7
e) um número maior que 6
n(A) = 3
)(
)(
)(
En
An
AP
P(A) =
3
6
= 0,50 ou 50%
b) EVENTO DESEJADO
A = {2, 4, 6}

4. c) EVENTO DESEJADO (> 2)
A = {3, 4, 5, 6 }
n(A) = 4
)(
)(
)(
En
An
AP P(A) =
4
6
= 0,6666….
n(A) = 6
)(
)(
)(
En
An
AP
P(A) =
6
6
= 1 ou 100%
d) EVENTO DESEJADO (< 7)
A = {1, 2, 3, 4, 5, 6}
EVENTO CERTO
e) EVENTO DESEJADO (> 6)
A = { }
n(A) = 0
P(A) =
0
6
= 0
)(
)(
)(
En
An
AP
EVENTO
Impossível

5. Exercício 2:
Em um sorteio envolvendo os números naturais de 1 a 5000, a probabilidade de
neste sorteio sair um número que seja múltiplo de cinco é:
ESPAÇO AMOSTRAL
E = {1, 2, 3, ….., 4998, 4999, 5000}
EVENTO DESEJADO
A = {5, 10, 15,…, 4990, 4995, 5000 }
n(A) = ?
n(E) = 5000
)(
)(
)(
En
An
AP
n(A) = 1000
an = a1 + (n – 1).r
P.A!
5000 = 5 + (n – 1).5
5000 = 5 + 5n – 5
1000 = n
P(A) =
1000
5000
= 0,20
x 100
20%

6. Exercício 3:
Uma urna contém 5 bolas brancas e 20 pretas. A probabilidade de
sortearmos uma bola branca é de:
ESPAÇO AMOSTRAL
E = {B, B, B, B, B, P, P, P……..,P}
EVENTO DESEJADO
A = {B, B, B, B, B}
n(A) = 5
n(E) = 25
)(
)(
)(
En
An
AP
P(A) =
5
25
= 0,20
x 100
20%

7. Exercício 4:
A probabilidade de uma bola branca aparecer ao se retirar uma única
bola de uma urna contendo 4 bolas brancas, 3 vermelhas e 5 azuis, é:
ESPAÇO AMOSTRAL
E = {B, B, B, B, V, V, V, A, A, A, A, A}
EVENTO DESEJADO
A = {B, B, B, B }
n(E) = 4
n(E) = 12
)(
)(
)(
En
An
AP
P(A) =
4
12
= 0,333…
x 100
33%

8. Exercício 5:
Joga-se dois dados. Qual a probabilidade de obtermos, nas faces
voltadas para cima, a soma 9.:
ESPAÇO AMOSTRAL
E = {(1,1), (1,2), (1, 3),…...….
(6, 4),…….(6,5), ….(6,6)}
EVENTO DESEJADO
A = {(3,6); (4, 5); (5, 4); (6, 3)}
n(A) = 4
n(E) = 36
)(
)(
)(
En
An
AP
P(A) =
4
36
= 0,11…
x 100
11%

9.  Matheus Martins