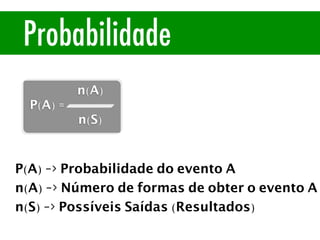
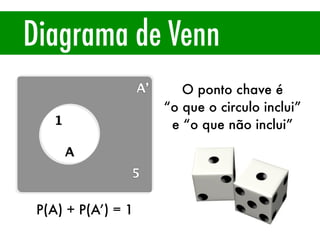
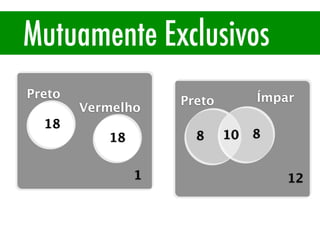
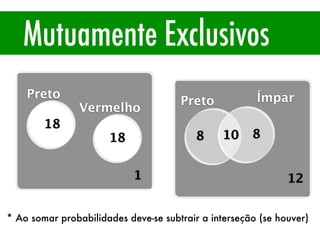
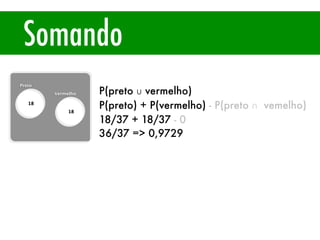
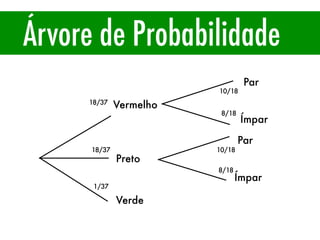
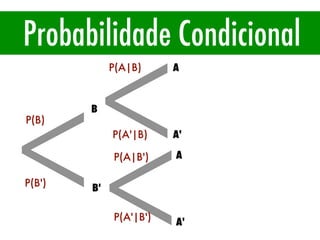
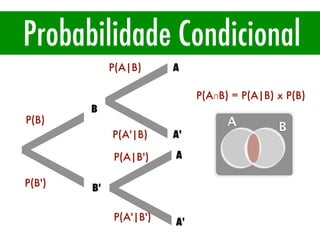
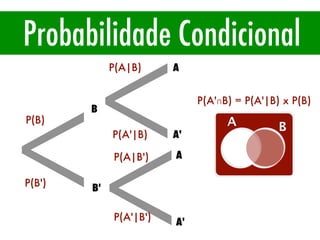
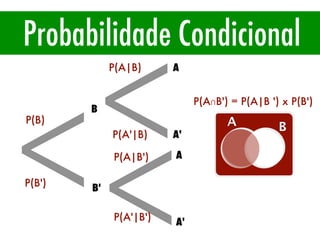
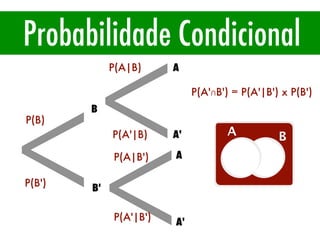
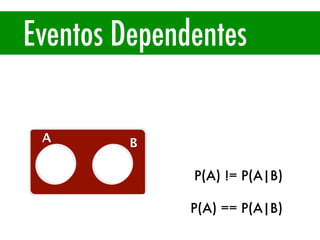
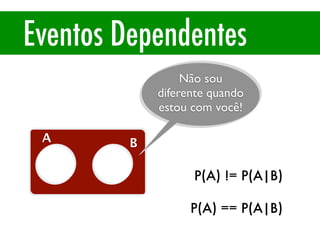
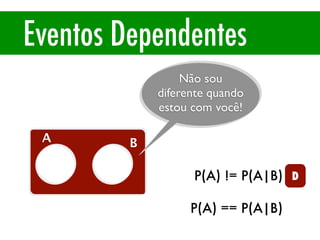
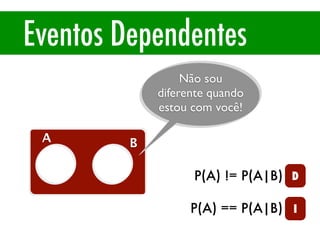
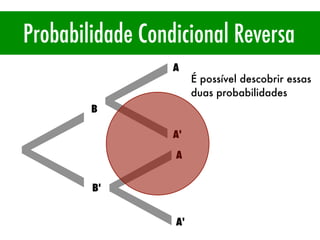
O documento apresenta conceitos básicos de estatística e probabilidade, incluindo média, mediana, moda, probabilidade, eventos dependentes e independentes. Discute como calcular a probabilidade de eventos e introduz os conceitos de probabilidade condicional e reversa.

1. Estatística Básica
Probabilidade
André Faria Gomes

2. Recapitulando...
Média
Mediana
Moda
Outliers
Amplitude
Variância
Desvio Padrão
Z-Score

3. Agenda
Introdução à Probabilidade
Probabilidade Condicional
Probabilidade Condicional Reversa (Bayes)
Eventos Dependentes e Independentes

5. Como medir
quais são as
chances de algo
acontecer?

6. Sempre
quis saber qual a
probabilidade de
ganhar na loteria!
Como medir
quais são as
chances de algo
acontecer?

7. Sempre
quis saber qual a
probabilidade de
ganhar na loteria!
Como medir
quais são as
chances de algo
acontecer?
Probabilidade

8. Mede-se a probabilidade numa escala de 0 a 1

9. Um evento impossível tem probabilidade 0.
Mede-se a probabilidade numa escala de 0 a 1

10. Um evento impossível tem probabilidade 0.
Mede-se a probabilidade numa escala de 0 a 1
Um vento com absoluta certeza tem probabilidade 1.

11. P(A) =
n(A)
n(S)
Probabilidade
P(A) -> Probabilidade do evento A
n(A) -> Número de formas de obter o evento A
n(S) -> Possíveis Saídas (Resultados)

12. A
5
Diagrama de Venn
1
O ponto chave é
“o que o circulo inclui”
e “o que não inclui”
A’
P(A) + P(A’) = 1

13. Calculando...

14. Calculando...
P(3) = 1 / 6

15. Calculando...
P(3) = 1 / 6
P(3) = 0,16666667

16. Calculando...
P(3) = 1 / 6
P(3) = 0,16666667
P(3) = 16%

17. Calculando...
P(3) = 1 / 6
P(3) = 0,16666667
P(3) = 16%
P(PAR) = 3 / 6

18. Calculando...
P(3) = 1 / 6
P(3) = 0,16666667
P(3) = 16%
P(PAR) = 3 / 6
P(PAR) = 0.5

19. Calculando...
P(3) = 1 / 6
P(3) = 0,16666667
P(3) = 16%
P(PAR) = 3 / 6
P(PAR) = 0.5
P(PAR) = 50%

20. Roleta

21. Roleta
18 Pretos

22. Roleta
18 Pretos
18 Vemelhos

23. Roleta
18 Pretos
18 Vemelhos
1 Verde

24. Roleta
18 Pretos
18 Vemelhos
1 Verde
P(0) = 1 / 37

25. Roleta
18 Pretos
18 Vemelhos
1 Verde
P(0) = 1 / 37
P(0) = 0.027027

26. Roleta
18 Pretos
18 Vemelhos
1 Verde
P(0) = 1 / 37
P(0) = 0.027027
P(0) = 2,7%

27. Beleza!
Quer dizer que a
minha chance de ganhar é
bem menor que a de
perder....

28. Beleza!
Quer dizer que a
minha chance de ganhar é
bem menor que a de
perder....

29. Beleza!
Quer dizer que a
minha chance de ganhar é
bem menor que a de
perder....
Isso, Isso,
Isso! Mas lembre-se que
a probabilidade é apenas um
indicador. Não uma
garantia.

30. Beleza!
Quer dizer que a
minha chance de ganhar é
bem menor que a de
perder....
Isso, Isso,
Isso! Mas lembre-se que
a probabilidade é apenas um
indicador. Não uma
garantia.
Mesmo que
pouco provável ainda
sim, um evento pode
acontecer!

31. Roleta
P(verde) = 0,027027
P(vermelho) = 0,48648
P(preto) = 0,48648
Probabilidade de não vermelho
P(vermelho') = 1 - 0,48648
P(vermelho') = 0,513513
P(vermelho') = 1 - P(vermelho)

32. Roleta
1
Preto
Vermelho
18
18

33. Mutuamente Exclusivos
Preto
Vermelho
18
18 8 8
10
Preto Ímpar
12
1

34. Mutuamente Exclusivos
Preto
Vermelho
18
18 8 8
10
Preto Ímpar
* Ao somar probabilidades deve-se subtrair a interseção (se houver)
12
1

35. Somando
Preto
Vermelho
18
18
P(preto ∪ vermelho)
P(preto) + P(vermelho) - P(preto ∩ vemelho)
18/37 + 18/37 - 0
36/37 => 0,9729

36. Somando
Preto
Vermelho
18
18
P(preto ∪ vermelho)
P(preto) + P(vermelho) - P(preto ∩ vemelho)
18/37 + 18/37 - 0
36/37 => 0,9729
8 8
10
Preto
Ímpar
P(preto ∪ impar)
P(preto) + P(impar) - P(preto ∩ impar)
18/37 + 18/37 - 10/37
26/37 => 0,7027

37. Probabilidade Condicional

38. Probabilidade Condicional

39. Probabilidade Condicional
Mas se
você já sabe que a bola
caiu em uma casa preta qual
a probabilidade de ser
ímpar?

40. Probabilidade Condicional
8 8
10
Preto
Ímpar
P(A|B) = P(A ∩ B) / P(B)
P(A|B) = 10 / 18
P(A|B) = 0,556
Mas se
você já sabe que a bola
caiu em uma casa preta qual
a probabilidade de ser
ímpar?

41. Probabilidade Condicional
P(A|B) ≠ P(B|A)
P(A|B) = obter A dado que B já ocorreu
P(B|A) = obter B dado que A já ocorreu

42. Probabilidade Condicional
P(A|B) ≠ P(B|A)
P(A|B) = obter A dado que B já ocorreu
P(B|A) = obter B dado que A já ocorreu

43. Árvore de Probabilidade
Vermelho
Preto
Verde
1/37
18/37
18/37
Par
Ímpar
Par
Ímpar
10/18
10/18
8/18
8/18

44. Probabilidade Condicional
<
P(B)
P(B')
B
B'
<
<
A
A'
A
A'
P(A|B)
P(A'|B)
P(A|B')
P(A'|B')

45. Probabilidade Condicional
P(A∩B) = P(A|B) x P(B)
<
P(B)
P(B')
B
B'
<
<
A
A'
A
A'
P(A|B)
P(A'|B)
P(A|B')
P(A'|B')
A B

46. Probabilidade Condicional
<
P(B)
P(B')
B
B'
<
<
A
A'
A
A'
P(A|B)
P(A'|B)
P(A|B')
P(A'|B')
P(A'∩B) = P(A'|B) x P(B)
A B
Probabilidade Condicional

47. Probabilidade Condicional
<
P(B)
P(B')
B
B'
<
<
A
A'
A
A'
P(A|B)
P(A'|B)
P(A|B')
P(A'|B')
P(A∩B') = P(A|B ') x P(B')
A B

48. Probabilidade Condicional
<
P(B)
P(B')
B
B'
<
<
A
A'
A
A'
P(A|B)
P(A'|B)
P(A|B')
P(A'|B')
P(A'∩B') = P(A'|B') x P(B')
A B

49. Probabilidade Condicional
P(B) = P(B ∩ A) + P(B ∩ A')
P(A∩B) = P(A|B) x P(B)
P(A'∩B) = P(A'|B) x P(B)
A = Preto
B = Ímpar
P(A∩B) = P(A|B) x P(B)
P(A∩B) = 10/18 x 18/37
P(A∩B) = 10/37
P(A∩B) = 0,27

50. Eventos Dependentes
A B
P(A) != P(A|B)
P(A) == P(A|B)

51. Eventos Dependentes
A B
Não sou
diferente quando
estou com você!
P(A) != P(A|B)
P(A) == P(A|B)

52. Eventos Dependentes
A B
Não sou
diferente quando
estou com você!
P(A) != P(A|B)
P(A) == P(A|B)
D

53. Eventos Dependentes
A B
Não sou
diferente quando
estou com você!
P(A) != P(A|B)
P(A) == P(A|B)
D
I

54. Eventos Independentes
É mais fácil trabalhar com eventos independentes!
P(A) == P(A|B)
P(A|B) == P(A∩B) ÷ P(B)
P(A∩B) = P(A) x P(B)
você já sabe que
mas dado que
então

55. Eventos Independentes
É mais fácil trabalhar com eventos independentes!
P(A) == P(A|B)
P(A|B) == P(A∩B) ÷ P(B)
P(A∩B) = P(A) x P(B)
você já sabe que
mas dado que
então

56. Eventos Independentes
É mais fácil trabalhar com eventos independentes!
P(A) == P(A|B)
P(A|B) == P(A∩B) ÷ P(B)
P(A∩B) = P(A) x P(B)
você já sabe que
mas dado que
então
Qual a
probabilidade de a
bola cair duas vezes
na casa preta na
roleta?

57. Probabilidade Condicional
Em uma escola com 60% de meninos e 40% de meninas .
As meninas usam calças e saias em números iguais, todos
os meninos usam somente calças. Bolha vê um estudante a
distancia, e vê que está usando calças. Qual é a
probabilidade do estudante ser menina?
Fonte: http://en.wikipedia.org/wiki/Bayes'_theorem

58. Probabilidade Condicional
Probabilidade Condicional Reversa
P(A|B) = P(A ∩B) / P(B)
Teorema de Bayes

59. Probabilidade Condicional
Probabilidade Condicional Reversa
P(A|B) = P(A ∩B) / P(B)
Teorema de Bayes

60. Probabilidade Condicional
Até agora encontramos
A|B em uma arvore de
probabilidade que já
conhecíamos. E quando não a
conhecemos?
Probabilidade Condicional Reversa
P(A|B) = P(A ∩B) / P(B)
Teorema de Bayes

61. Probabilidade Condicional
Até agora encontramos
A|B em uma arvore de
probabilidade que já
conhecíamos. E quando não a
conhecemos?
Probabilidade Condicional Reversa
P(A|B) = P(A ∩B) / P(B)
Teorema de Bayes

62. Probabilidade Condicional
Probabilidade Condicional Reversa
P(A|B) = P(A ∩B) / P(B)
<
B
B'
<
<
A
A'
A
A'
É possível descobrir essas
duas probabilidades

63. Probabilidade Condicional
A
B
Menina
Calças
P(A|B)
Probabilidade de o estudante ser
menina dado que está usando calças

64. Probabilidade Condicional
A
B
Menina
Calças
P(A|B)
Probabilidade de o estudante ser
menina dado que está usando calças

65. Probabilidade Condicional
P(A|B)
Há 40% de meninas e 60% de meninos
P(A) = 0,4
Meninas vestem tanto calças quanto saias
P(B|A) = 0,5
50% das garotas e 100% dos garotos vestem calças.
P(B) = 0,5 × 0,4 + 1,0 × 0,6 = 0,8

66. Probabilidade Condicional
P(A|B)

67. Probabilidade Condicional
P(A|B)

68. Probabilidade Condicional
P(A|B)
Só 25% de
chance de ser uma
garota... Melhor não
arriscar!

69. Obrigado!!!