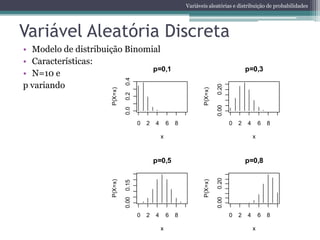
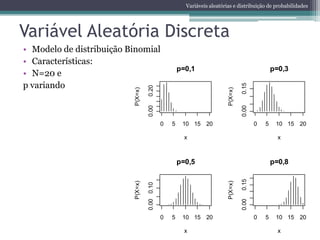
O documento apresenta uma aula sobre bioestatística. Aborda conceitos como variáveis quantitativas e qualitativas, apresentação de dados em gráficos e tabelas, medidas de tendência central e variabilidade, noções de probabilidade e cálculo de probabilidades, incluindo espaço amostral, eventos, probabilidade de eventos e soma de probabilidades. Também introduz conceitos sobre variáveis aleatórias discretas e distribuição de Bernoulli.







































![Variáveis aleatórias e distribuição de probabilidades
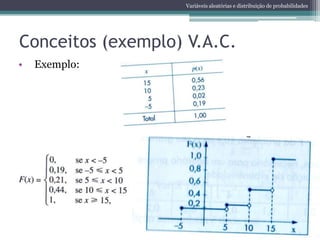
Conceitos V. A. C.
2. Variância de uma v.a. significa o quanto os dados
variam em relação a média.
Assim, se X for uma v.a que assume valores x1, ,xn, então
a variância da v.a. X é dada por:
Var( X ) ( x E ( X ))2 f ( x)dx
2 2
Var( X ) E ( X ) [ E ( X )]](https://image.slidesharecdn.com/aula2-educaofsica-120509173023-phpapp02/85/Aula-2-educacao-fisica-43-320.jpg)