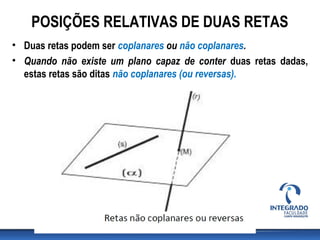
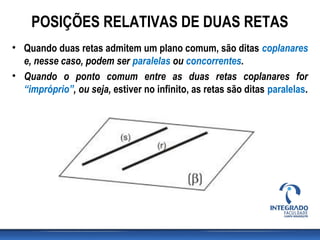
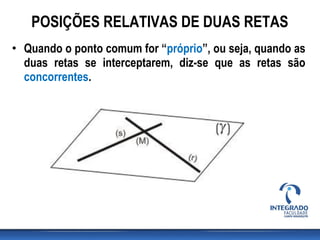
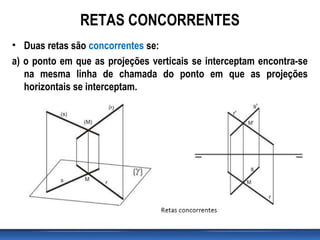
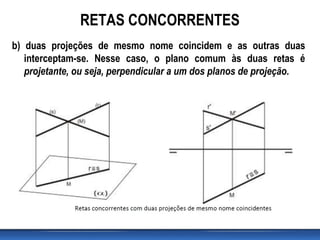
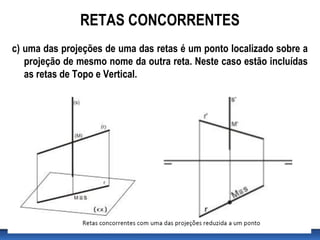
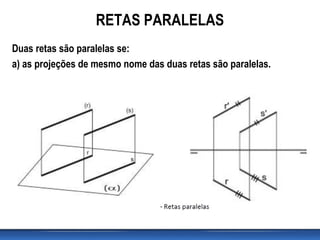
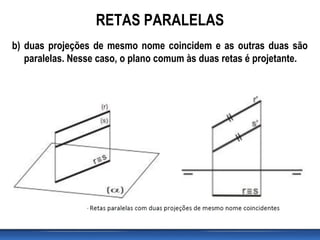
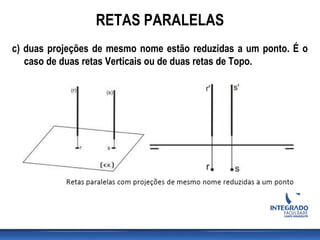
Este documento discute posições relativas de retas em geometria descritiva. Ele explica que duas retas podem ser coplanares ou não coplanares, e que retas coplanares podem ser paralelas ou concorrentes. O documento também fornece critérios para determinar se duas retas são paralelas ou concorrentes e inclui exercícios para identificar posições relativas de retas.

1. AULA 21
GEOMETRIA DESCRITIVA
Professor: João Alessandro
ESTUDO DA RETA
PARTE 2

2. POSIÇÕES RELATIVAS DE DUAS RETAS
• Duas retas podem ser coplanares ou não coplanares.
• Quando não existe um plano capaz de conter duas retas dadas,
estas retas são ditas não coplanares (ou reversas).

3. • Quando duas retas admitem um plano comum, são ditas coplanares
e, nesse caso, podem ser paralelas ou concorrentes.
• Quando o ponto comum entre as duas retas coplanares for
“impróprio”, ou seja, estiver no infinito, as retas são ditas paralelas.
POSIÇÕES RELATIVAS DE DUAS RETAS

4. • Quando o ponto comum for “próprio”, ou seja, quando as
duas retas se interceptarem, diz-se que as retas são
concorrentes.
POSIÇÕES RELATIVAS DE DUAS RETAS

5. RETAS CONCORRENTES
• Duas retas são concorrentes se:
a) o ponto em que as projeções verticais se interceptam encontra-se
na mesma linha de chamada do ponto em que as projeções
horizontais se interceptam.

6. b) duas projeções de mesmo nome coincidem e as outras duas
interceptam-se. Nesse caso, o plano comum às duas retas é
projetante, ou seja, perpendicular a um dos planos de projeção.
RETAS CONCORRENTES

7. c) uma das projeções de uma das retas é um ponto localizado sobre a
projeção de mesmo nome da outra reta. Neste caso estão incluídas
as retas de Topo e Vertical.
RETAS CONCORRENTES

8. Duas retas são paralelas se:
a) as projeções de mesmo nome das duas retas são paralelas.
RETAS PARALELAS

9. b) duas projeções de mesmo nome coincidem e as outras duas são
paralelas. Nesse caso, o plano comum às duas retas é projetante.
RETAS PARALELAS

10. c) duas projeções de mesmo nome estão reduzidas a um ponto. É o
caso de duas retas Verticais ou de duas retas de Topo.
RETAS PARALELAS

11. EXERCÍCIOS
1) Determinar a posição relativa entre as retas (E)(F) e (G)(H).
Dados:
(E) [ 0 ; 2 ; 2 ] (G) [ 0 ; -1 ; 3]
(F) [ 4 ; 2 ; 4 ] (H) [ 4 ; -1 ; 5 ]
2) Determinar a posição relativa entre as retas (I)(J) e (K)(L).
Dados:
(I) [ 0 ; 4 ; -1 ] (K) [ 1 ; 2,5 ; 0,5 ]
(J) [ 6 ; 1 ; 2 ] (L) [ 6 ; 2,5 ; 0,5 ]

12. 3) Determinar a posição relativa entre as retas (A)(B) e (C)
(D). Dados:
(A) [ 1 ; 2 ; 2 ] (C) [ 0 ; 4 ; 0,5 ]
(B) [ 6 ; 3 ; 1 ] (D) [ 5 ; 2 ; 3 ]
4) Por um ponto (O), traçar uma reta paralela à reta (M)(N).
Dados:
(M) [ 1 ; 1,5 ; 1 ] (O) [ 3 ; -1 ; -3,5]
(N) [ 5 ; 1,5 ; 2,5 ]
EXERCÍCIOS

13. REFERÊNCIAS BIBLIOGRÁFICAS
• Cruz, D. C.; Amaral, L. G. H. do. APOSTILA DE GEOMETRIA
DESCRITIVA. UFBA. Barreiras, Bahia, 2012.
• PRÍNCIPE JUNIOR, A. dos R. Noções de Geometria Descritiva.
v.1. São Paulo: Nobel, 1983.
• MONTENEGRO, G. Geometria descritiva. v.1. São Paulo: Edgard
Blücher, 2004.

14. DÚVIDAS?
joaoalessandro.luz@gmail.com