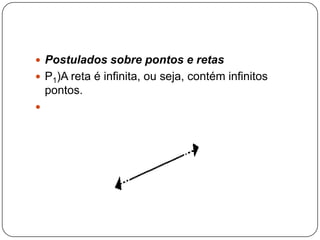
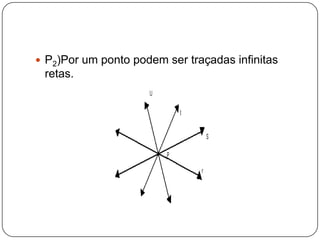
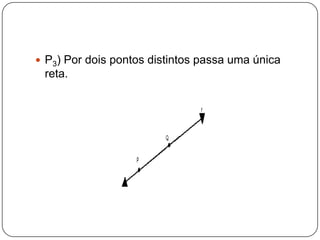
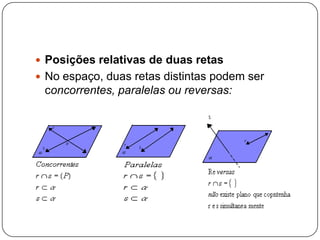
[1] O documento apresenta os conceitos básicos da geometria espacial, incluindo pontos, retas, planos e suas posições relativas no espaço tridimensional. [2] Aborda também os axiomas e postulados sobre esses elementos geométricos, bem como a definição de ângulos diedrais formados por planos concorrentes. [3] Tem como objetivo fornecer uma introdução aos principais conceitos e propriedades da geometria no espaço.

1. GEOMETRIA ESPACIALALUNAS: Denise; Luana Ramos e ThaísNº 05,15,253º ”A”

2. IntroduçãoA Geometria espacial (euclidiana) funciona como uma ampliação da Geometria plana (euclidiana) e trata dos métodos apropriados para o estudo de objetos espaciais assim como a relação entre esses elementos. Os objetos primitivos do ponto de vista espacial, são: pontos, retas, segmentos de retas, planos, curvas, ângulos e superfícies. Os principais tipos de cálculos que podemos realizar são: comprimentos de curvas, áreas de superfícies e volumes de regiões sólidas. Tomaremos ponto, reta e plano como conceitos primitivos, os quais serão aceitos sem definição.

3. Conceitos primitivos São conceitos primitivos ( e, portanto, aceitos sem definição) na Geometria espacial os conceitos de ponto, reta e plano.

4. Axiomas Axiomas, ou postulados (P), são proposições aceitas como verdadeiras sem demonstração e que servem de base para o desenvolvimento de uma teoria. Temos como axioma fundamental:existem infinitos pontos, retas e planos.

5. Postulados sobre pontos e retasP1)A reta é infinita, ou seja, contém infinitos pontos.

6. P2)Por um ponto podem ser traçadas infinitas retas.

7. P3) Por dois pontos distintos passa uma única reta.

8. Posições relativas de duas retasNo espaço, duas retas distintas podem ser concorrentes, paralelas ou reversas:

9. Um plano no espaço R3 pode ser determinado por qualquer uma das situações:Três pontos não colineares (não pertencentes à mesma reta).Um ponto e uma reta ou um segmento de reta que não contém o ponto.Um ponto e um segmento de reta que não contém o ponto.Duas retas paralelas que não se sobrepõe.Dois segmentos de reta paralelos que não se sobrepõe.Duas retas concorrentes.Dois segmentos de reta concorrentes.

10. Posições entre planosPlanos concorrentes no espaço R3 são planos cuja interseção é uma reta.Planos paralelos no espaço R3 são planos que não tem interseção.Diedro: Quando dois planos são concorrentes, dizemos que tais planos formam um diedro.

11. Exemplo

12. Ângulo diedral: É ângulo formado por dois planos concorrentes. Para obter o ângulo diedral, basta tomar o ângulo formado por quaisquer duas retas perpendiculares aos planos concorrentes.Planos normais são aqueles cujo ângulo diedral é um ângulo reto (90 graus).