O documento apresenta o Sistema de Avaliação da Educação do Estado do Rio de Janeiro (Saerj) que avaliou alunos em 2013 nas áreas de Língua Portuguesa e Matemática. O Saerj vem sendo aplicado desde 2006 e tem ajudado a melhorar a qualidade do ensino no estado através do fornecimento de diagnósticos.










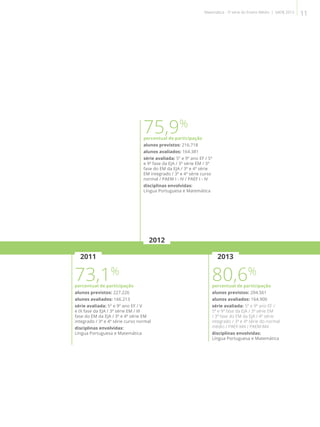



























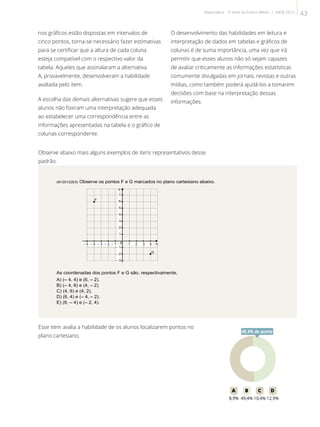


![(M120445ES) O gráfico abaixo representa uma função definida no intervalo [– 4, 6].
7
8
Essa função é decrescente no intervalo
A) [– 4, 0]
B) [0, 2]
C) [0, 6]
D) [0, 8]
E) [2, 6]
Esse item avalia a habilidade de os alunos analisarem crescimento e
decrescimento de funções reais apresentadas em gráficos.
Para resolvê-lo, eles devem identificar o intervalo do domínio no
qual a função é decrescente. Nesse caso, eles devem associar o
intervalo de decrescimento da função ao intervalo [-4, 0]. Os alunos
que assinalaram a alternativa A, provavelmente, desenvolveram a
habilidade avaliada pelo item.
Os alunos que marcaram a alternativa B, provavelmente, não se
apropriaram do significado de decrescimento de uma função,
confundindo com seu crescimento. Aqueles que assinalaram a
alternativa C, possivelmente, não compreenderam o comando do
item, marcando o complementar da resposta, ou seja, justamente o
intervalo no qual a função não é decrescente. Os alunos que optaram
pela alternativa D, provavelmente, compreenderam o enunciado do
item, entretanto, fizeram, de forma equivocada, a correspondência do
intervalo do domínio em que a função decresce com a imagem desse
intervalo. Já a escolha pela alternativa E sugere que tais respondentes
não compreendem o significado de decrescimento de uma função,
40A B C D E
40,7% 18,3% 9,4% 20,7%9,8%
40,7% de acerto
47Matemática - 3ª série do Ensino Médio | SAERJ 2013](https://image.slidesharecdn.com/provasaerjmatemticaterceiroano-141114195053-conversion-gate02/85/Prova-saerj-matematica-terceiro-ano-47-320.jpg)