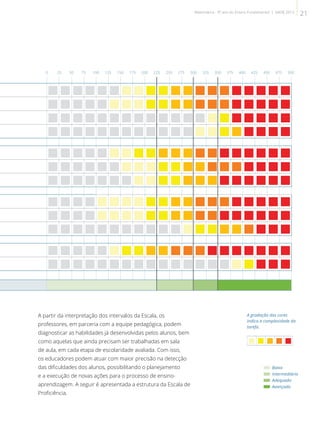
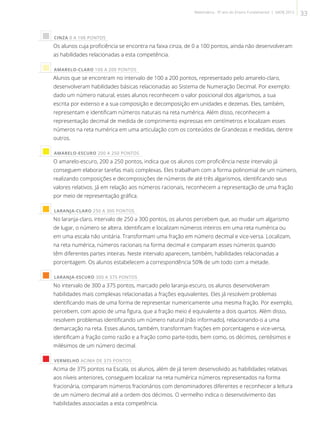
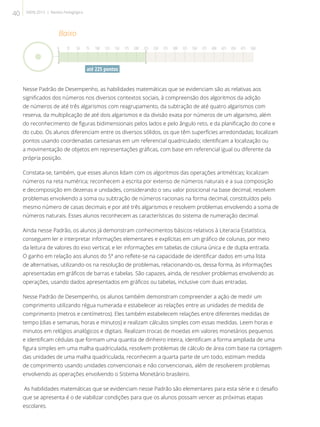
O documento apresenta o Sistema de Avaliação da Educação do Estado do Rio de Janeiro (Saerj), que avaliou alunos em 2013 nas áreas de Língua Portuguesa e Matemática. O Saerj tem se consolidado ao longo dos anos, fornecendo informações sobre o desempenho dos alunos para apoiar políticas educacionais.