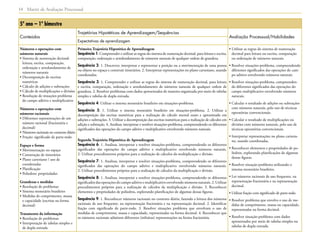
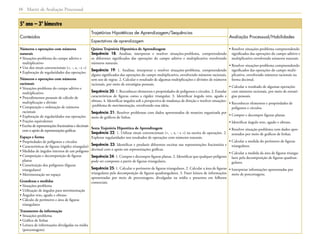
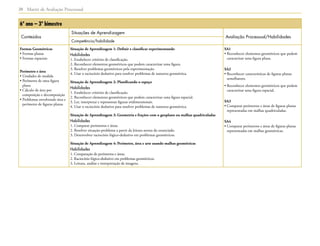
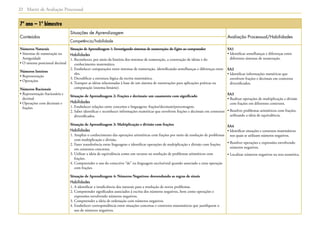
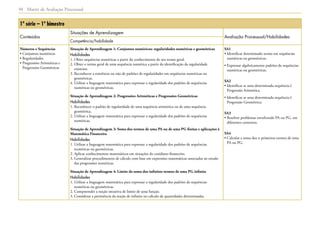
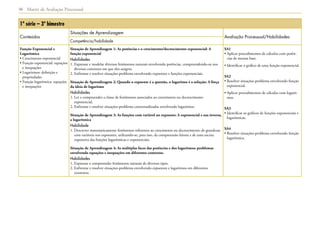
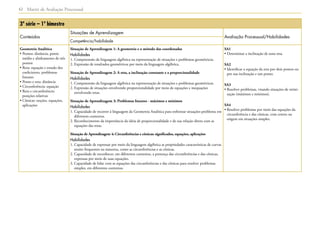
1) O documento apresenta as matrizes de referência para a avaliação processual nas disciplinas de Língua Portuguesa, Matemática e outras nos anos iniciais, finais do Ensino Fundamental e Ensino Médio.
2) As matrizes definem os conteúdos, competências e habilidades que devem ser desenvolvidos ao longo do percurso escolar e orientar a elaboração das provas de avaliação da aprendizagem em processo.
3) As matrizes visam apoiar professores e gestores na implementação do currículo oficial e