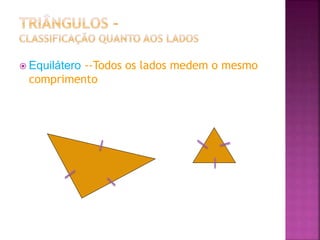
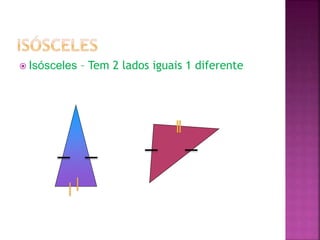
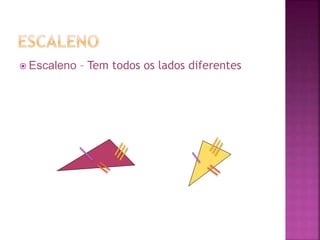
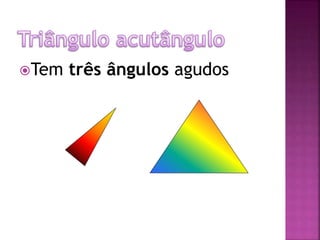
O documento discute conceitos geométricos básicos como retas, segmentos de reta, ângulos e triângulos. Ele define o que são retas, semi-retas e segmentos de reta e como representá-los. Também explica os tipos de ângulos e como medir ângulos. Por fim, classifica triângulos de acordo com o tamanho de seus lados e ângulos internos e estabelece que a soma dos ângulos internos de um triângulo é sempre 180 graus.

1. Rectas , semi-rectas e
segmentos de recta
Ângulos
Triângulos

2.  linha sem princípio nem fim
A
G
r
Representa-se = NOTAÇÃO
AG os dois pontos da recta em letra maiúscula
Ou r designação de recta por uma letra minúscula

3.  Tem princípio e não tem fim
A
J
Como tem início no ponto A e
passa pelo ponto J ,
representa-se pela NOTAÇÃO =
ÅJ

4.  É um conjunto de pontos, tem inicio num ponto e
finda noutro ponto
A
B
Representa-se pela NOTAÇÃO:
• [AB], lê-se o segmento de recta AB (coloca-se o ponto de
inicio A e de fim B entre parênteses rectos
•AB – lê-se comprimento do segmento de recta ( coloca-se
um traço por cima das letras que definem o segmento de
recta
•exemplo AB = 3 cm

5.  Rectas concorrentes - tem um ponto em
comum
s
r
Rectas oblíquas
s é oblíqua a r
m
t
m é perpendicular a t
NOTAÇÃO m t
A recta m ao cruzar-se com t divide o
plano em 4 partes iguais, formando
um ângulo de 90º

6.  Duas rectas do plano dizem-se paralelas
quando:
Não têm pontos em comum
NOTAÇÃO m // v
Lê-se: m paralela a v
m
v
p
n São coincidentes n e p

7.  Um ângulo é a porção compreendida entre
duas semi-rectas com a mesma origem
 NOTAÇÃO:
 O ângulo UOV =
 A amplitude (medida) do ângulo
 Mede-se a amplitude de um ângulo com o
transferidor

8. Å Ů
P
Um ângulo diz-se raso
se mede 180º.

9.  Para medir a amplitude de um ângulo:
 Fazer coincidir o centro do transferidor com o vértice do
ângulo
 Sobrepor as linhas dos zeros
a um dos lados do ângulo
 Ler a medida da amplitude no outro lado do ângulo
Escreve-se DÊF = 40º Escreve-se PÂR = 125º
A

10.  Para desenhar o ângulo STU com 70º
 Desenhar uma semi-recta ŤU
 Fazer coincidir o centro do
transferidor com o ponto T
(vértice do ângulo)
 A partir do zero, medir 70º e assinalar
 Traçar a semi-recta com origem em T
passando no ponto assinalado e nessa
semi-recta marcar o ponto S.

11.  Podem-se estudar em relação:
 Ao comprimento dos lados
 À amplitude dos ângulos internos

12.  Equilátero --Todos os lados medem o mesmo
comprimento

13.  Isósceles – Tem 2 lados iguais 1 diferente

14.  Escaleno – Tem todos os lados diferentes

15.  Tem um ângulo recto outros dois agudos

16.  Tem um ângulo obtuso e os outros dois
agudos

17. Tem três ângulos agudos

18.  Cortam-se os três ângulos internos de um
triângulo
 Juntam-se os ângulos recortados
 Obtém-se um ângulo raso
ou seja 180º
 Logo a soma dos ângulos internos de um
Triângulo é de 180º