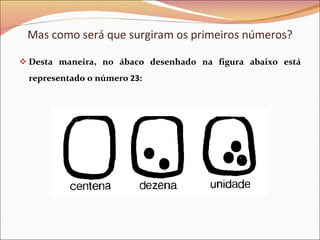
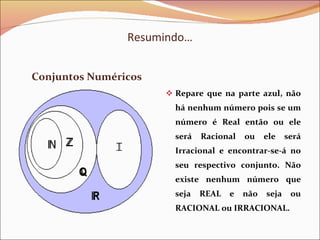
O documento descreve a evolução histórica dos números, desde os primeiros sistemas de contagem usados por humanos primitivos até o desenvolvimento dos diferentes conjuntos numéricos. Os egípcios criaram um dos primeiros sistemas de numeração com símbolos e os hindus introduziram o zero para representar classes vazias no ábaco. Pitágoras descobriu os números irracionais ao tentar medir a diagonal de um quadrado. Finalmente, surgiram os números reais, que englobam todos os outros conjuntos numéricos.