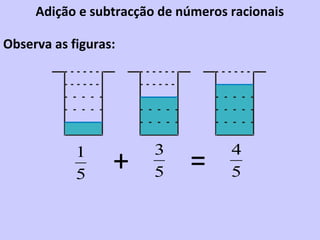
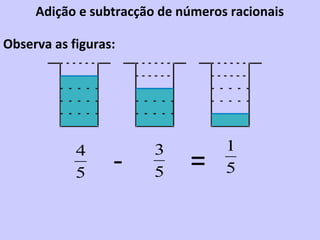
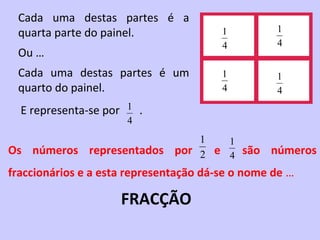
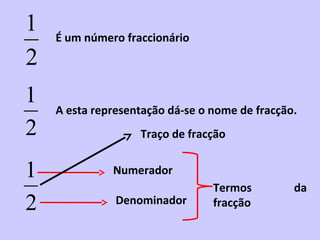
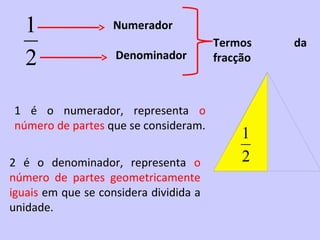
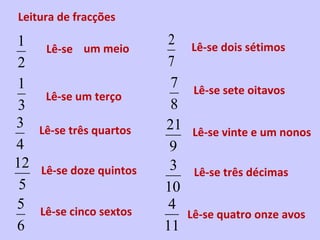
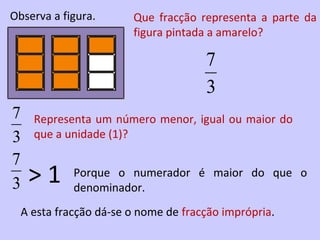
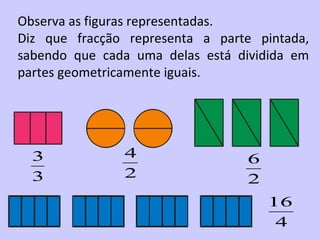
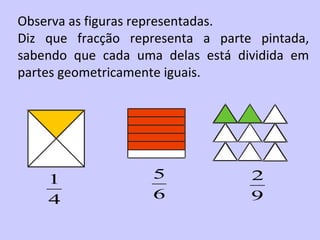
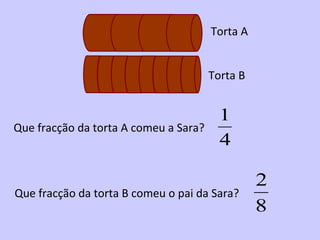
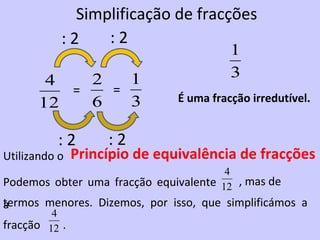
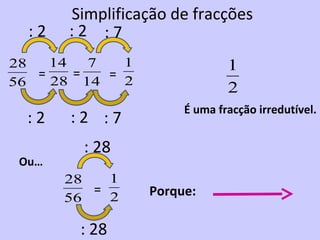
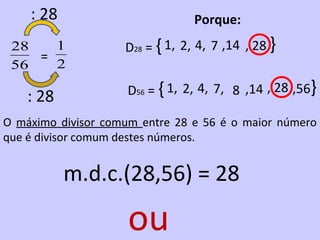
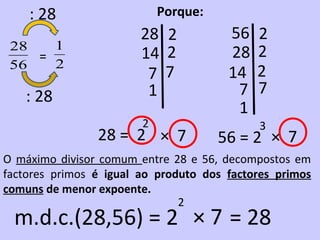
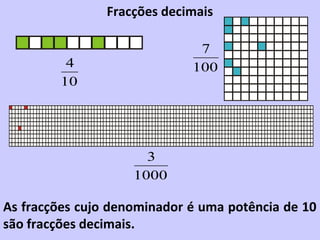
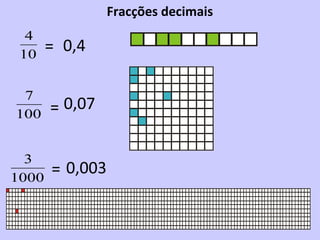
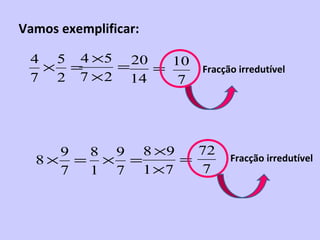
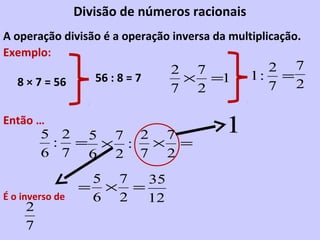
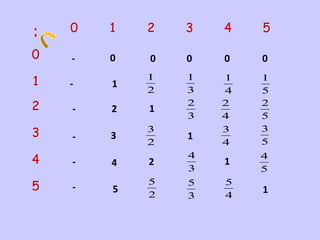
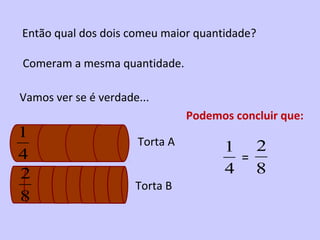
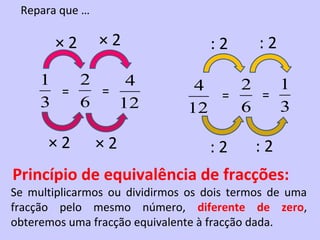
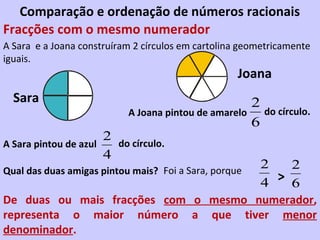
1) O documento apresenta conceitos sobre números racionais, incluindo números inteiros, fracionários e operações com frações. 2) É introduzido o conceito de fração como uma forma de representar partes de um todo através de um numerador e denominador. 3) São apresentadas regras para comparar e ordenar frações, dependendo de terem o mesmo denominador, mesmo numerador ou diferentes.

1. NÚMEROS RACIONAIS
5 1 1
6 2 +
7 2 3
11
2,34
12 2
5− 3×
5 4 1
÷ 5
3 7 Teresa Nascimento
Zulmira Castro Lobo

2. NÚMEROS FRACCIONÁRIOS
A Sara quis fazer um painel que representasse as quatro
estações do ano.
1
Começou por dividi-lo em 2
duas partes geometricamente 1
iguais.
2
Cada uma destas partes do painel é uma metade do
painel.
1
E representa-se por:
2

3. A seguir, a Sara dividiu, por sua vez, cada uma das metades do
painel também em duas partes geometricamente iguais.
Obteve o painel dividido em quatro partes geometricamente
iguais.

4. Cada uma destas partes é a
quarta parte do painel. 1 1
4 4
Ou …
Cada uma destas partes é um 1 1
quarto do painel. 4 4
E representa-se por 1 .
4
1 1
Os números representados por 2 e 4 são números
fraccionários e a esta representação dá-se o nome de …
FRACÇÃO

5. A parte do painel que representa o
Inverno e o Verão corresponde a
metade do painel e é, por isso,
representada por:
1
1:2 ou
2
1
É o quociente exacto da divisão de 1 por 2.
2
Como,
1 : 2 = 0,5 logo …
1
= 0,5
2
0,5 é, também, o quociente exacto da divisão de 1 por 2.

6. Assim, o número fraccionário um meio pode representar-
se por:
1
(fracção)
2
ou
0,5 (numeral decimal)

7. Pensemos no número fraccionário um quarto.
1 1 1
=1:4 e
4 4 4
1 : 4 = 0,25 1
1
4
1 4
Logo, = 0,25
4
Portanto, este número, um quarto, pode representar-se
por: 1
(fracção)
4
ou
0,25 (numeral decimal)

8. 1 É um número fraccionário
2
1
A esta representação dá-se o nome de fracção.
2 Traço de fracção
1 Numerador
Termos da
2 Denominador fracção

9. 1 Numerador
Termos da
2 Denominador fracção
1 é o numerador, representa o
número de partes que se consideram.
1
2 é o denominador, representa o 2
número de partes geometricamente
iguais em que se considera dividida a
unidade.

10. Leitura de fracções
1 Lê-se um meio 2 Lê-se dois sétimos
2 7
1 7 Lê-se sete oitavos
Lê-se um terço
3 8
3 Lê-se três quartos 21 Lê-se vinte e um nonos
4 9
12 Lê-se doze quintos 3 Lê-se três décimas
5 10
5 Lê-se cinco sextos 4
Lê-se quatro onze avos
6 11

11. Observa a figura que vai ser dividida em três partes
geometricamente iguais.
1
3
A parte pintada de vermelho corresponde a …
1
3

12. 1
=1:3
3
1 : 3 = 0, 3333…
O quociente que vai aparecendo em cada momento
0,3 ; 0,33 ; 0, 333 ; 0,3333 e assim sucessivamente
É uma aproximação, por defeito, do quociente da
divisão de 1 por 3.

13. Como 0, 3333… não é um quociente exacto, não
podemos representar o número um terço por um
numeral decimal.
Por isso, representamo-lo por: 1
3
Estes novos números, os NÚMEROS FRACCIONÁRIOS,
vieram tornar sempre possível a operação divisão.

14. 1 Representa um número menor, igual ou maior do
que a unidade (1)?
3
1
3 <1 Porque o numerador é menor do que o
denominador.
A esta fracção dá-se o nome de fracção própria.

15. Fracções que representam números inteiros
Observa os três rectângulos geometricamente
iguais, divididos em partes geometricamente
iguais.
Que fracção representa a parte pintada de
amarelo?
2 4 8
2 4 8
2 4 8
= 1 =1 =1
2 4 8

16. Cada uma das fracções:
2 4 8
2 4 8
Representam a unidade (1).
2:2=1 4:4=1 8:8=1
O numerador e o denominador de cada uma delas
são representados pelo mesmo número.

17. Observa a figura. Que fracção representa a parte da
figura pintada a amarelo?
7
3
7 Representa um número menor, igual ou maior do
3 que a unidade (1)?
7
3 >1 Porque o numerador é maior do que o
denominador.
A esta fracção dá-se o nome de fracção imprópria.

18. Observa as figuras representadas.
Diz que fracção representa a parte pintada,
sabendo que cada uma delas está dividida em
partes geometricamente iguais.
3 4 6
3 2 2
16
4

19. 3 Estas fracções representam
= 1
3 números inteiros.
4
= 2 És capaz de definir uma regra que
2 permita verificar se uma fracção
6 representa um número inteiro?
= 3
2
Uma fracção representa um
número inteiro se o numerador
16
= 4 for múltiplo do denominador.
4

20. Observa as figuras representadas.
Diz que fracção representa a parte pintada,
sabendo que cada uma delas está dividida em
partes geometricamente iguais.
1 5 2
4 6 9

21. Será que estas fracções representam números
inteiros?
1 5 2
4 6 9
Não!
Representam números … FRACCIONÁRIOS.
Porque …
Nestas fracções o numerador NÃO É múltiplo do
denominador.

22. O que é então um número racional?
1 6
3
4 2
3
Qualquer número que se possa representar por
uma fracção ou por uma razão é um número
racional.
NOTA: Razão é o mesmo que quociente.
Assim, qualquer número inteiro ou fraccionário é
um número racional.

23. Observa a recta numérica.
Coloca na recta os seguintes números racionais.
2 4 15 8 5 11
5 5 5 5 5 5
5 8 11
5 5 5
0 2 4 1 2 3
15
5 5
5

24. Agora já podemos preencher a tabela de dupla entrada
da divisão utilizando números inteiros.

25. : 0 1 2 3 4 5
0 - 0 0 0 0 0
1 - 1
1 1 1 1
2 3 4 5
2 - 2 1
2 2 2
3 4 5
3 - 3
3
1
3 3
2 4 5
4 - 4 2
4
1
4
3 5
5
5 - 5
5 5
1
2 3 4

26. Fracções equivalentes
A mãe da Sara fez duas deliciosas tortas de chocolate (que
são iguais).
À sobremesa, dividiu uma delas em quatro fatias iguais e a
outra em oito, tal como mostra a figura.
Torta A A Sara comeu uma
fatia da torta A e o
pai comeu duas
Torta B fatias da torta B.
Qual dos dois comeu maior porção de torta?

27. Torta A
Torta B
1
Que fracção da torta A comeu a Sara?
4
2
Que fracção da torta B comeu o pai da Sara?
8

28. Então qual dos dois comeu maior quantidade?
Comeram a mesma quantidade.
Vamos ver se é verdade...
Podemos concluir que:
1
Torta A 1 2
4 =
2 4 8
Torta B
8

29. 1 2
=
4 8
Estas fracções representam a mesma porção…
Dizem-se, por isso, fracções equivalentes.
As fracções que representam o mesmo número chamam-
se fracções equivalentes.

30. Princípio de equivalência de fracções
Vamos observar as figuras:
Que fracção representa
a parte pintada, de
4
cada uma das figuras?
12
Podemos concluir que:
2
6
1 2 4
1 = =
3 6 12
3

31. Repara que …
×2 ×2 :2 :2
1 2 4 4 2 1
= = = =
3 6 12 12 6 3
×2 ×2 :2 :2
Princípio de equivalência de fracções:
Se multiplicarmos ou dividirmos os dois termos de uma
fracção pelo mesmo número, diferente de zero,
obteremos uma fracção equivalente à fracção dada.

32. Simplificação de fracções
:2 :2
1
4 2 1 3
= =
12 6 3 É uma fracção irredutível.
:2 :2
Utilizando o Princípio de equivalência de fracções
4
Podemos obter uma fracção equivalente 12 , mas de
termos menores. Dizemos, por isso, que simplificámos a
a
4
fracção 12 .

33. Simplificação de fracções
:2 :2 :7
28 14 7 1 1
= = = 2
56 28 14
2
É uma fracção irredutível.
:2 :2 :7
: 28
Ou…
28 1
= Porque:
56 2
: 28

34. : 28 Porque:
28 1 D28 = { 1, 2, 4, 7 ,14 , 28 }
=
56 2
: 28 D56 = { 1, 2, 4, 7, 8 ,14 , 28 ,56}
O máximo divisor comum entre 28 e 56 é o maior número
que é divisor comum destes números.
m.d.c.(28,56) = 28
ou

35. : 28 Porque:
28 2 56 2
28 1
= 14 2 28 2
56 2
7 7 14 2
: 28 1 7 7
1
2 3
28 = 2 × 7 56 = 2 × 7
O máximo divisor comum entre 28 e 56, decompostos em
factores primos é igual ao produto dos factores primos
comuns de menor expoente.
2
m.d.c.(28,56) = 2 × 7 = 28

36. Comparação e ordenação de números racionais
Fracções com o mesmo denominador
A Sara e a Joana estão a comer dois chocolates.
Sara Joana
3 1
A Sara já comeu A Joana já comeu
5 5
3 1
Qual é a mais gulosa? É a Sara, porque >
5 5
De duas ou mais fracções com o mesmo denominador,
representa o maior número a que tiver maior numerador.

37. Comparação e ordenação de números racionais
Fracções com o mesmo numerador
A Sara e a Joana construíram 2 círculos em cartolina geometricamente
iguais.
Joana
Sara 2
A Joana pintou de amarelo do círculo.
6
2
A Sara pintou de azul do círculo.
4
Qual das duas amigas pintou mais? Foi a Sara, porque
2 2
4 > 6
De duas ou mais fracções com o mesmo numerador,
representa o maior número a que tiver menor
denominador.

38. Comparação e ordenação de números racionais
Fracções denominador e numerador diferentes
A Sara e o João comeram o que falta dos dois chocolates.
Sara João
Qual dos dois amigos comeu maior quantidade de
chocolate?
5
A Sara comeu do chocolate.
8
2
O João comeu do chocolate.
3

39. A Sara comeu
5 2
do chocolate e o João comeu do chocolate.
8 3
5 2 M8: 0, 8, 16, 24, 32, …
8 3 M3: 0, 3, 6, 9, 12, 15, 18, 21, 24, 27, …
(3) (8)
Então, vamos escrever fracções equivalentes a
15 16 5 2
e com denominador 24.
24 24 8 3
m.m.c.(8,3) = 24
5 2
Logo < Então quem comeu mais chocolate?
8 3 Foi o João!
15 16
porque 24 < 24

40. Fracções decimais
7
4 100
10
3
1000
As fracções cujo denominador é uma potência de 10
são fracções decimais.

41. Fracções decimais
4
10
= 0,4
7
100 = 0,07
3
1000
= 0,003

42. Adição e subtracção de números racionais
Observa as figuras:
1
5
+ 3
5 = 4
5

43. Adição e subtracção de números racionais
Observa as figuras:
1
4
5 - 3
5 = 5

44. Adição e subtracção de números racionais
= - =
4
+
1 3 4 3 1
5 5 5 5 5 5
Para adicionar ou subtrair dois números representados por
fracções com o mesmo denominador, adicionam-se ou
subtraem-se os numeradores e o denominador mantém-se.

45. Adição e subtracção de números racionais
m.m.c.(6,4) = 12
5 3
+ = M6: 0, 6, 12, 18, 24, …
6 4
(2) (3)
M4: 0, 4, 8, 12, 16, 20, …
10 9
= + = Então, vamos escrever fracções equivalentes a
12 12
5 e 3
19 com denominador 12.
= 6 4
12

46. Multiplicação de números racionais
A Maria comeu metade de um chocolate.
1
2
O Paulo comeu a quarta parte de um chocolate igual ao da
Maria .
1
4
Logo o Paulo comeu metade de metade do chocolate que a
Maria comeu .
1 1
Ou seja, o Paulo comeu de
2 2

47. 1 1
de É o mesmo que
2 2
1 1 1 Como se multiplicaram estes
× =
2 2 4 dois números?
Multiplicámos os numeradores e multiplicámos os
denominadores.
Então:
Para multiplicar dois números representados por
fracções, multiplicam-se os numeradores um pelo
outro e multiplicam-se os denominadores, também,
um pelo outro.

48. Vamos exemplificar:
4 5 4 ×5 20 10
× = = = Fracção irredutível
7 2 7 × 2 14 7
9 8 9 8 ×9 72
8× = × = = Fracção irredutível
7 1 7 1 ×7 7

49. Continuando a exemplificar…
5 6 5 6 ×5 30
0,6 × = × = = =1
3 10 3 10 ×3 30
4 7 4
× = =2
7 2 2
Generalizando…
a b a ×b
× =
c d c ×d

50. Potência de um número racional
7 4 = × 7 ×7 ×7 = 49 ×49 = 2401
7
3
2  2 2 2 2 ×2 ×2 8
  = × × = =
3  3 3 3 3 ×3 ×3 27
3
2  2
  É a base
3  3
3 É o expoente

51. Inverso de um número racional
Dado um número racional diferente de zero, é sempre
possível encontrar outro número que multiplicado pelo
primeiro dê de produto a unidade (1).
1 1
8 × =1 O inverso de 8 é e vice-versa.
8 8
6 5 6 5
× =1 O inverso de é e vice-versa.
5 6 5 6
Generalizando…
a b
× =1
b a

52. Divisão de números racionais
A operação divisão é a operação inversa da multiplicação.
Exemplo:
2 7 2 7
8 × 7 = 56 56 : 8 = 7 × =1 1: =
7 2 7 2
Então …
5 2 5 7 2 7 1
: = × : × =
6 7 6 2 7 2
5 7 35
= × =
É o inverso de 6 2 12
2
7

53. Para dividir dois números racionais, diferentes de zero,
multiplica-se o dividendo pelo inverso do divisor
5 2 5 7 35
: == × =
6 7 6 2 12
Generalizando…
a b
: = a ×d
c d c b