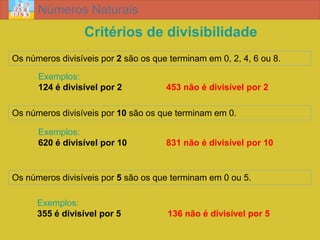
O documento discute propriedades e operações com números naturais, incluindo: 1) identidade fundamental da adição e multiplicação, 2) potências e regras de prioridade, 3) critérios de divisibilidade, 4) decomposição em fatores primos, 5) números primos e compostos, e 6) cálculo do mínimo múltiplo comum e máximo divisor comum.