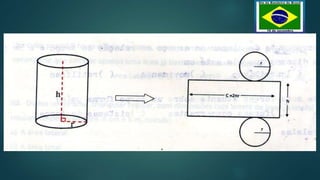
O documento discute os conceitos de cilindro, incluindo o cálculo de áreas e volumes. Explica como calcular a área da circunferência, área do retângulo, área lateral e área total de um cilindro. Também mostra como calcular o volume de um cilindro e de um prisma retangular. Apresenta exemplos de cálculos de áreas e volumes em diferentes situações.

1. CILINDRO
 INTRODUÇÃO
 COMPRIMENTO DA CIRCUNFERÊNCIA
 ÁREA DO RETÂNGULO
 ÁREA DA CIRCUNFERÊNCIA
 ÁREA LATERAL
 ÁREA DA BASE
 ÁREA TOTAL
 VOLUME DO CILINDRO

2. INTRODUÇÃO
NA FIGURA QUE REPRESENTA O CONGRESSO
NACIONAL, TEMOS OS DOIS PRÉDIO COM UM
FORMATO DE UM PARALELEPÍPEDO, E DUAS CÚPULAS
QUE SE ASSEMELHAM A DUAS
SEMICIRCUNFERÊNCIAS CASO QUISÉSSEMOS
CALCULAR A ÁREA TOTAL DESSAS FIGURAS
GEOMÉTRICAS TERÍAMOS QUE CALCULAR AS ÁREAS
DOS PRISMAS E DOS DOIS CORPOS REDONDOS.

4. Lei de formação
 COMPRIMENTO DA CIRCUNFERÊNCIA C 2ΠR
 ÁREA DA CIRCUNFERÊNCIA A Π𝑅2
 ÁREA DO RETÂNGULO A BASE ALTURA
A B X H

5. Observando a planificação do cilindro,
temos uma melhor visualização das
partes que compõem um cilindro.
Agora ficou mais fácil resolver os
cálculos das áreas laterais e total do
cilindro. Vamos tentar?

7. Área da base de raio R A = 𝜋𝑅2
Área lateral: área do retângulo formado pela
planificação do cilindro de dimensões 𝐴𝑙 =
2𝜋𝑅. ℎ
Área total Área lateral 2Área da base
𝐴 𝑡 𝐴𝑙 2𝐴 𝑏
ou
𝐴 𝑡 𝐴𝑙 2𝐴 𝑏 𝐴 𝑡 2𝜋𝑅. ℎ 2𝜋𝑅2
𝐴 𝑡 2𝜋. 𝑅(𝑅 + ℎ)

8. Observe essas duas piscinas:
Ao analisarmos essas duas piscinas observe que os
formatos são distintos, em uma piscina o formato é
circular e no outro o formado da piscina é
retangular. Isso faz com que o cálculo do volume
de ambas as piscinas sejam feitas de formas
distintas. Em ambos os casos o cálculo do volume
pode ser calculado pelo produto da área da base
pela altura, a diferença nos dois casos são
juntamente as bases das figuras, isso dá a distinção
do cálculo do volume em ambas as piscinas.

10. Cálculo do volume do cilindro:
No caso da piscina de base circular, o
cálculo do volume é feito da seguinte
forma:
Volume Área da base altura
V 𝐴 𝑏(𝑐𝑚2) h(cm)
V 𝜋𝑅2(𝑐𝑚2) h(cm)
V 𝜋𝑅2
h(𝑐𝑚3
)

11. Cálculo do volume do prisma retangular:
Agora vamos pensar na segunda piscina, onde
o formato é retangular, o cálculo é bem mais
simples:
Volume comprimento(cm) altura(cm)
largura (cm)
Volume a(cm) b(cm) c(cm), então V
a b c (𝑐𝑚3
)

12. Exercícios:
1) (ENEM – 2018)

13. 2) ENEM 2010 -
Dona Maria, diarista na casa da
Teixeira, precisa fazer café para servir
as vinte pessoas que se
encontram numa reunião na sala.
fazer o café, Dona Maria dispõe de
uma leiteira cilíndrica e copinhos
plásticos, também cilíndricos.

14. Com o objetivo de não desperdiçar café, a diarista deseja colocar a quantidade
mínima de água na leiteira para encher os vinte copinhos pela metade. Para que
isso ocorra, Dona Maria deverá
A) encher a leiteira até a metade, pois ela tem um volume 20 vezes maior que o
volume do copo.
B) encher a leiteira toda de água, pois ela tem um volume 20 vezes maior que o
volume do copo.
C) encher a leiteira toda de água, pois ela tem um volume 10 vezes maior que o
volume do copo.
D) encher duas leiteiras de água, pois ela tem um volume 10 vezes maior que o
volume do copo.
E) encher cinco leiteiras de água, pois ela tem um volume 10 vezes maior que o
volume do copo.

15. 3)(Banestes - Banco do Estado do Espirito
Santo - ES – 2018 – Analista Econômico
Financeiro – Gestão Contábil)
Certos tambores para coleta de resíduos não recicláveis são
cilindros com 40 cm de diâmetro e 60 cm de altura.
O volume de um desses recipientes, em litros, é de,
aproximadamente:
a) 75
b) 90
c) 120
d) 150
e) 180

16. 4) (SAP-SP – 2018 - Secretaria de
Administração Penitenciária -
Analista administrativo)
Em uma fazenda, foi construído um silo na forma cilíndrica, com
base medindo 4m e altura medindo 12m, para armazenar cereais.
Utilizando π =3, qual o volume desse silo?
a) 144 m2
b 216 m2
c) 288 m2
d) 576 m2
e) 1728 m2

17. 5) (SEDUC-PI -2018
Professor Temporário – Matemática)
A figura seguinte é um recipiente cilíndrico reto, e contém água até a
metade de sua altura. Uma esfera maciça, colocada no seu interior,
fica totalmente submersa, elevando a altura da água em 2 cm. Qual o
volume dessa esfera?
a) 16π cm3
b) 20π cm3
c) 24π cm3
d) 28π cm3
e) 32π cm3

18. 6) (EEAR – Escola de Sargento da Aeronáutica –
2018 – Controlado de Tráfego Aéreo – Turma 1)
Na ilustração a seguir, são apresentadas duas situações. Na primeira, o cilindro
contém um líquido que atinge uma altura h. Inserindo-se uma esfera de 3 cm de
raio nesse mesmo cilindro, o nível do líquido aumenta, conforme situação 2. O novo
volume, determinado pelo líquido somado à esfera, totaliza 588cm3 .
Considerando π = 3 e o raio da base do cilindro igual a 4 cm, a medida da altura h
corresponde a ______ cm.
a) h = 8
b) h = 10
c) h = 16
d) h = 32

20. FIM
Prof: José Américo