Baixado 47 vezes
Carregado porProfessor Carlinhos
GEOMETRIA DA POSIÇÃO
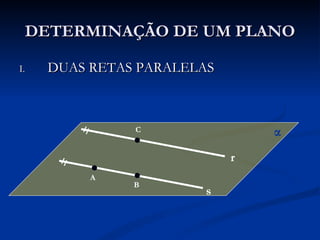
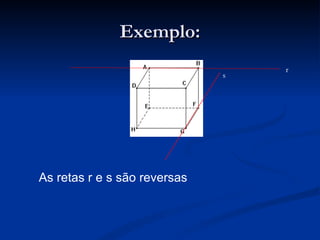
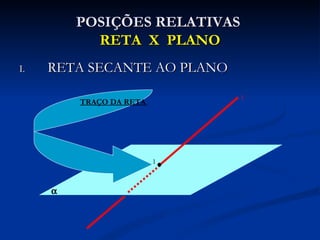
O documento discute a geometria espacial e as relações entre pontos, retas e planos no espaço. Apresenta três axiomas fundamentais e descreve como determinar e analisar as posições relativas de retas e planos, que podem ser concorrentes, paralelas ou reversas.
Mais conteúdo relacionado
Semelhante a GEOMETRIA DA POSIÇÃO
GEOMETRIA DA POSIÇÃO
- 1. GEOMETRIA DA POSIÇÃO AGeometria espacial (euclidiana) funciona como uma ampliação da Geometria plana (euclidiana) e trata dos métodos apropriados para o estudo de objetos espaciais assim como a relação entre esses elementos. PONTO RETA PLANO
- 2. AXIOMA 1 DADOS DOISPONTOS DISTINTOS NO ESPAÇO, EXISTE UMA E SOMENTE UMA, RETA QUE OS CONTÊM. AXIOMA 2 DADOS TRÊS PONTOS DISTINTOS E NÃO COLINEARES NO ESPAÇO, EXISTE UM E APENAS UM, PLANO QUE OS CONTÊM.
- 3. AXIOMA 3 SE UMARETA POSSUI DOIS DE SEUS PONTOS NUM PLANO, ELA ESTÁ CONTIDA NESSE PLANO.
- 4. DETERMINAÇÃO DE UMPLANO AXIOMA 2 UMA RETA “ S ” E UM PONTO P NÃO PERTENCENTE A RETA S. s α P A B
- 5. DETERMINAÇÃO DE UMPLANO I. DUAS RETAS CONCORRENTES. s α A P B r
- 6. DETERMINAÇÃO DE UMPLANO I. DUAS RETAS PARALELAS C α r A B s
- 7. POSIÇÕES RELATIVAS RETA X RETA CASO 1 : CONCORRENTES s s P P r r Duas retas são concorrentes se elas têm um ponto em comum. As retas perpendiculares são retas concorrentes que formam entre si um ângulo reto.
- 8. POSIÇÕES RELATIVAS RETA X RETA CASO 2 : PARALELAS r // s r s α Duas retas são paralelas se elas não possuem interseção e estão em um mesmo plano.
- 9. POSIÇÕES RELATIVAS RETA X RETA CASO 3 : REVERSAS Duas retas são ditas reversas quando uma não tem interseção com a outra e elas não são paralelas. Isto significa que elas estão em planos diferentes. D B C A
- 10. Exemplo: r s As retas r e s são reversas
- 11. POSIÇÕES RELATIVAS RETA X PLANO I. RETA CONTIDA NO PLANO α
- 12. POSIÇÕES RELATIVAS RETA X PLANO I. RETA SECANTE AO PLANO TRAÇO DA RETA r P α
- 13. POSIÇÕES RELATIVAS RETA X PLANO I. RETA PARALELA AO PLANO s r β A α Uma reta s é paralela a um plano α no espaço R3, se existe uma reta r inteiramente contida no plano que é paralela à reta dada.
- 14. POSIÇÕES RELATIVAS PLANO X PLANO Planos concorrentes no espaço R3 são planos cuja interseção é uma reta. β r B α A
- 15. POSIÇÕES RELATIVAS PLANO X PLANO Planos paralelos no espaço R3 são planos que não tem interseção. r β s α
- 16.