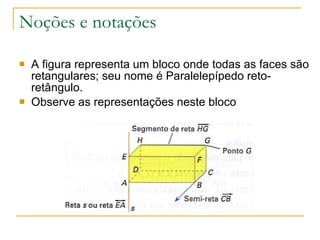
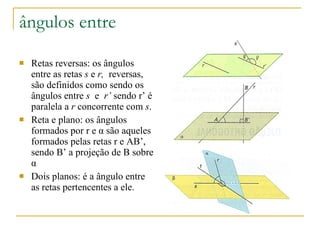
1) O documento discute conceitos fundamentais de geometria de posição, incluindo definições de retas, planos, ângulos e posições relativas entre esses objetos geométricos. 2) É apresentado um paralelepípedo retangular como exemplo para ilustrar seções planas e posições relativas entre faces e planos. 3) Conceitos como paralelismo, perpendicularidade e projeção ortogonal entre retas e planos são explicados.

1. Mate‘mágica’, de novo Só que vai dificultando

2. Hoje: Geometria de posição Secções planas: (Pergunta lá pro Sal a diferença entre seção, secção e sessão) A maioria dos objetos a nossa volta não é plana. Seccionar, é ‘cortar’ e uma secção é uma parte do que foi cortado. Secção plana é a figura resultante na superfície de separação entre as secções.

3. A geometria de Posição estuda as figuras geométricas quanto à sua forma e posição, e a Geometria métrica as estuda em relação as suas medidas. Vamos destacar os conceitos fundamentais da GP, necessários para o desenvolvimento da GM.

4. Noções e notações A figura representa um bloco onde todas as faces são retangulares; seu nome é Paralelepípedo reto-retângulo. Observe as representações neste bloco

5. Dois pontos distintos, determinam uma única reta. Duas retas distintas determinam um único ponto Todo ponto pertencente a uma reta, divide-a em duas partes. A reunião deste ponto com qualquer uma das partes se chama semi-reta. Cada face do paralelepípedo é parte de um plano, que continua infinitamente alem dos limites da face. Duas retas não coincidentes, determinam um plano Três pontos não colineares, determinam no mínimo três retas. E por tanto esses três pontos também determinam um plano.

6. Toda reta contida em um plano, divide-o em duas partes. A reunião dessa reta com qualquer uma das partes determina um semi-plano Dois planos três retas, coplanares duas a duas, determinam três planos. Três planos determinam um espaço Espaço é a reunião de todos os pontos

7. Posições relativas entre: retas Duas retas no espaço podem ser: Paralelas: se, somente se, são coplanares e não tem nenhum ponto em comum(paralelas distintas) ou têm todos os pontos em comum(retas coincidentes) Concorrentes: se são coplanares e com um único ponto em comum. Reversas: se não existe um plano que contenha as duas simultaneamente. Ou seja, retas não-coplanares

8. Posições relativas entre: reta e plano Uma reta r e um plano α podem ser: r é paralela a α se, somente se, r e α não tem nenhum ponto em comum r está contida em α se todo ponto de r pertence a α r é secante ou concorrente a α se, r e α têm um único ponto em comum

9. Posições relativas entre: planos Dois planos são: Paralelos se não tem nenhum ponto em comum(paralelos distintos) ou se tem todos os ponto em comum(paralelos coincidentes) Secantes, se tem uma única reta em comum.

10. Perpendicularidade entre Retas: duas retas são perpendiculares, se forem concorrentes e formarem ângulos retos entre si. Reta e plano: Se todas as retas(na verdade só precisa de duas) do plano que concorrem com r forem perpendiculares a esta reta Planos: se existe um reta em um dos planos que seja perpendicular ao outro.

11. Projeção A Projeção Ortogonal de um ponto A sobre a reta/plano é o ponto A’ pertencente a reta/plano tal que AA’ ┴ a reta/plano.

12. ângulos entre Retas reversas: os ângulos entre as retas s e r, reversas, são definidos como sendo os ângulos entre s e r’ sendo r’ é paralela a r concorrente com s . Reta e plano: os ângulos formados por r e α são aqueles formados pelas retas r e AB’, sendo B’ a projeção de B sobre α Dois planos: é a ângulo entre as retas pertencentes a ele.

13. Um só.. Enorme. Mas que resume: