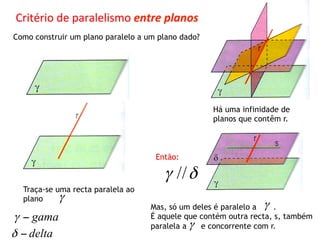
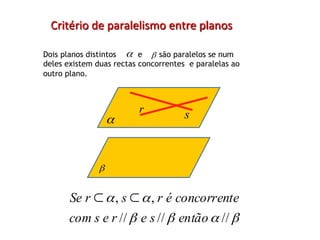
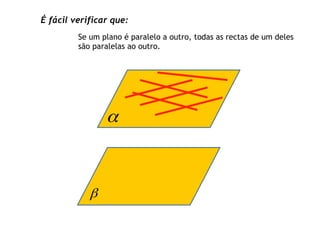
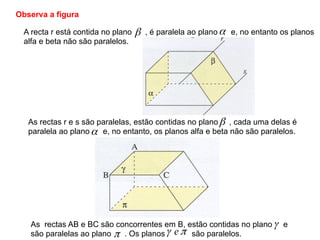
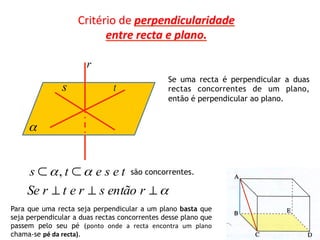
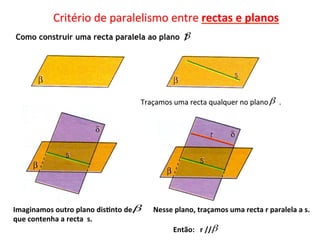
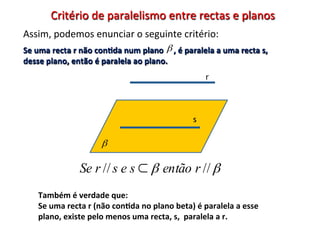
O documento descreve critérios de paralelismo e perpendicularidade entre retas e planos. Explica que uma reta é paralela a um plano se for paralela a outra reta contida nesse plano. Dois planos são paralelos se em um deles houver duas retas concorrentes e paralelas ao outro plano. Uma reta é perpendicular a um plano se for perpendicular a duas retas concorrentes desse plano.

1. Critérios de paralelismo
e de perpendicularidade

2. Critério
de
paralelismo
entre
rectas
e
planos
Como construir uma recta paralela ao plano β
?
Traçamos
uma
recta
qualquer
no
plano
β
.
Imaginamos
outro
plano
dis2nto
de
β
Nesse
plano,
traçamos
uma
recta
r
paralela
a
s.
que
contenha
a
recta
s.
β
Então:
r
//

3.
Critério
de
paralelismo
entre
rectas
e
planos
Assim,
podemos
enunciar
o
seguinte
critério:
uma
recta
r
não
con2da
num
plano
β
,
é
paralela
a
uma
recta
s,
Se
desse
plano,
então
é
paralela
ao
plano.
r
s
β
Se r // s e s ⊂ β então r // β
Também
é
verdade
que:
Se
uma
recta
r
(não
con2da
no
plano
beta)
é
paralela
a
esse
plano,
existe
pelo
menos
uma
recta,
s,
paralela
a
r.

4. Exercício:
B
A
figura
representa
um
paralelepípedo
rectângulo.
Jus2fica
que
a
recta
EF
é
paralela
à
face
[ABCD].
C

5. Critério
de
paralelismo
entre
planos
Como construir um plano paralelo a um plano dado?
Há uma infinidade de
planos que contêm r.
Então:
γ // δ
Traça-se uma recta paralela ao
plano γ
.
Mas, só um deles é paralelo a γ .
γ − gama É aquele que contém outra recta, s, também
paralela a γ e concorrente com r.
δ − delta

6. Critério
de
paralelismo
entre
planos
Dois planos distintos α e β são paralelos se num
deles existem duas rectas concorrentes e paralelas ao
outro plano.
r
α s
β
Se r ⊂ α , s ⊂ α , r é concorrente
com s e r // β e s // β então α // β

7. É fácil verificar que:
Se um plano é paralelo a outro, todas as rectas de um deles
são paralelas ao outro.
α
β

8. Exercício:
A figura representa o tronco de uma pirâmide.
As rectas AB e CD contidas no plano CAB são
paralelas ao plano EFG.
Podes concluir que os planos considerados são
paralelos?

9. Observa a figura
A recta r está contida no plano β , é paralela ao plano α e, no entanto os planos
alfa e beta não são paralelos.
As rectas r e s são paralelas, estão contidas no plano β , cada uma delas é
paralela ao plano α e, no entanto, os planos alfa e beta não são paralelos.
As rectas AB e BC são concorrentes em B, estão contidas no plano γ e
são paralelas ao plano π . Os planos γ e π são paralelos.

10. Critério
de
perpendicularidade
entre
recta
e
plano.
r
Se uma recta é perpendicular a duas
s t rectas concorrentes de um plano,
então é perpendicular ao plano.
α
s ⊂ α, t ⊂ α e s e t são concorrentes.
Se r ⊥ t e r ⊥ s então r ⊥ α
Para que uma recta seja perpendicular a um plano basta que
seja perpendicular a duas rectas concorrentes desse plano que
passem pelo seu pé (ponto
onde
a
recta
encontra
um
plano
chama-se pé
da
recta).

11. Critério
de
perpendicularidade
entre
recta
e
plano.

12. Exemplo:
A recta AC é perpendicular à recta CD do plano BCD e, no entanto, não é
perpendicular ao plano, pois teria que ser perpendicular a duas rectas
concorrentes e não a uma só.
Podemos afirmar que a recta AB é perpendicular ao plano BCD porque é
perpendicular a duas rectas concorrentes do plano: BE e BC.

13. Critério
de
perpendicularidade
entre
planos.
Se um plano contém uma recta perpendicular a outro plano, então
os dois planos são perpendiculares.
Reparem que estes dois planos
dividem o espaço em 4 regiões. A
cada uma chama-se DIEDRO.
DIEDRO é cada uma das quatro
regiões em que fica dividido o
espaço quando dois planos se
intersectam.
Se os quatro diedros forem iguais ,
os planos dizem-se PERPENDICULARES.
Caso contrário, os planos são OBLÍQUOS.
Se r ⊂ β e r ⊥ α então β ⊥ α

14. Na figura está representado um prisma hexagonal recto e regular.
Justifica as afirmações:
a) A recta AB é paralela ao plano CDE da base.
b) A recta BC é perpendicular aos planos das bases.
c) O plano BCD é perpendicular ao plano CDE.
d) O plano ABC é paralelo ao plano EFG.

15. Os
planos
β
,
γ
e
δ
,
são
perpendiculares
ao
plano
α