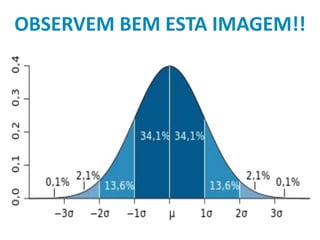
Este documento discute medidas de variabilidade e variação, definindo variabilidade como a diversificação dos valores de uma variável em torno de um valor central. Ele explica medidas como amplitude total, variância, desvio padrão e coeficiente de variação, fornecendo fórmulas e um exemplo de cálculo destas medidas para dados reais.

1. ESTATÍSTICA DESCRITIVA
Ranilson Oscar Araújo Paiva
Ranilson Oscar Araújo Paiva ranilsonpaiva@ic.ufal.br
MEDIDAS DE VARIABILIDADE

2. VARIABILIDADE E VARIAÇÃO

3.  O que é variabilidade?
 É a maior ou menor diversificação dos valores
de uma variável em torno de um valor de
tendência central.
 Para que servem as medidas de
variabilidade?
 São medidas utilizadas para caracterizar
valores de uma variável, ressaltando a
variabilidade entre esses valores e sua
medida de posição.

4.  Exemplo
 A = {70, 70, 70, 70, 70}
 B = {68, 69, 70, 71, 72}
 C = {5, 15, 50, 120, 160}
 Qual a média dos valores dos
conjuntos acima?
 Qual deles apresenta a maior
variabilidade?

5. MEDIDAS DE VARIABILIDADE

6.  Amplitude Total (Amostra)
 É a diferença entre o maior e menor valor de uma
amostra.
 Variância
 Determina o quão longe, em média, os valores de uma
amostra se encontram de um valor esperado.
 Desvio Padrão
 É a quantidade de variação que existe em relação à
média aritmética de uma amostra.
 Coeficiente de Variação
 É a estimativa de precisão de experimento, utilizada
para comparar distribuições diferentes.

7.  Amplitude Total (Amostra)
 Maior valor amostral – menor valor amostral.
 Desvio da Média
 Valor de um elemento da amostra – média aritmética.
 Desvio Quadrado
 Desvio da média elevado ao quadrado.
 Soma dos Quadrados
 Soma de todos os desvios quadrados de uma amostra.

8.  Variância
 Média aritmética dos desvios quadrados.
 Desvio Padrão
 Raiz quadrada da variância.
 Coeficiente de Variação
 É a razão entre o desvio padrão e a média.

9. FÓRMULAS
 Amplitude Total = max(n) – min(n)
 Variância (var) =
(𝑥 𝑖 − 𝑥)2
𝑛
 Desvio Padrão (σ) =
(𝑥 𝑖 − 𝑥)2
𝑛
 Coeficiente de Variação =
𝜎
𝑥

10. EXEMPLO
 QI dos Alunos Britânicos
 Consultar planilha com os dados
 Calcular:
 Média Aritmética
 Desvios da Média
 Desvios Quadrados
 Soma dos Quadrados
 Variância
 Desvio Padrão

11. OBSERVEM BEM ESTA IMAGEM!!

12. EXERCÍCIO (EST006)
 Consultar planilha com os dados dos alunos
 Link:
 Calcular:
 Média Aritmética
 Desvios da Média
 Desvios Quadrados
 Soma dos Quadrados
 Variância
 Desvio Padrão

13. LINKS RECOMENDADOS
 http://www.portalaction.com.br/estatistica-
basica/22-medidas-de-dispersao
 https://www.khanacademy.org/math/probabilit
y/descriptive-statistics#variance-std-deviation

14.  SOARES, J. F.; FARIAS, A. A.; CESAR, C. C.
Introdução à Estatística Básica.
 BUSSAD, W. O.; MORETTIN, P. A. Estatística
Básica.
 DEVORE, J. L. Probability and Statistics for
Engineering and the Sciences.
 CRESPO, Antônio – Estatística Fácil – 17ª ed. São
Paulo; Saraiva, 2002.
BIBLIOGRAFIA

15. Obrigado!
Dúvidas?