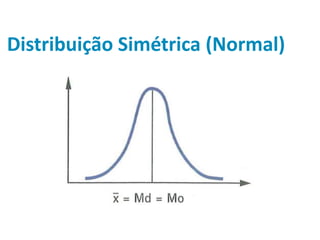
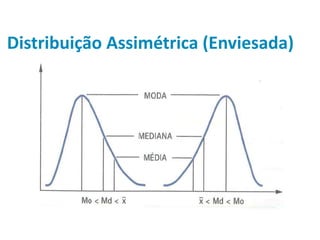
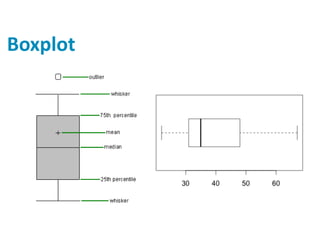
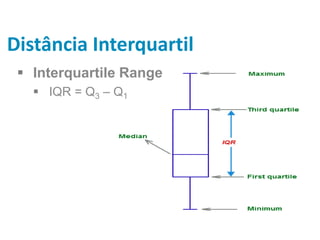
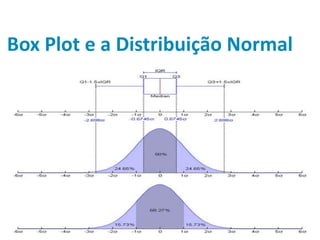
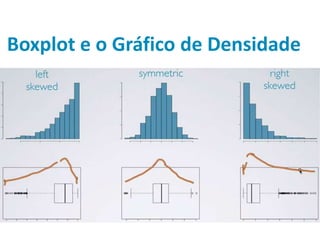
Este documento discute medidas estatísticas descritivas como assimetria, curtose e boxplot. Inclui definições de assimetria à esquerda e à direita usando coeficiente de assimetria de Pearson e explica curtose leptocúrtica, mesocúrtica e planticúrtica com o coeficiente percentílico de curtose. Também apresenta o boxplot e sua relação com a distribuição normal e o gráfico de densidade.

1. ESTATÍSTICA DESCRITIVA
Ranilson Paiva
Ranilson Paiva ranilsonpaiva@ic.ufal.br
MEDIDAS DE ASSIMETRIA,
CURTOSE E BOXPLOT

2. CONTEÚDO PROGRAMÁTICO
• INTRODUÇÃO À ESTATÍSTICA
• Estatística e Probabilidade, Grandes Áreas da Estatística
• Amostragem
• Estatística Descritiva e Estatística Inferencial
• Aplicações da Estatística na Engenharia
• Estatística Descritiva
• População e Amostra
• ESTATÍSTICA DESCRITIVA
• Apresentação e Agrupamento de Dados, Distribuições de Freqüência, Gráficos e
aplicações
• Medidas de Posição: Média, Mediana, Moda e Quartil
• Medidas de Dispersão: amplitude, desvio médio, variância, desvio-padrão, Coeficiente de
Variação e aplicações
• Medidas de Assimetria, Curtose e Boxplot
• Ditribuição Normal e Outliers

3. Agenda
 TEORIA
 Medidas de Assimetria
 Curtose
 Boxplot
• EXEMPLOS
 Medidas de Assimetria
 Curtose
 Boxplot
 Comparação com o gráfico de densidade
• EXERCÍCIOS
• LEITURA RECOMENDADA
• PERGUNTAS E RESPOSTAS
• REFERÊNCIAS

4. MEDIDAS DE ASSIMETRIA

5. Distribuição Simétrica (Normal)

6. Distribuição Assimétrica (Enviesada)

7. Medidas de Assimetria
 Tipo de Assimetria
 μ – Mo < 0
 Assimetria à Esquerda (Negativa)
 μ – Mo = 0
 Distribuição Simétrica (Normal)
 μ – Mo > 0
 Assimetria à Direita (Positiva)

8. Medidas de Assimetria
 Coeficiente de Assimetria de Pearson
 AS = 3 (μ- Md) / σ
 |AS| < 0.15
 Assimetria fraca
 0.15 < |AS| < 1
 Assimetria moderada
 |AS| > 1
 Assimetria forte
 Valor positivo = Assimetria à direita
 Valor negativo = Assimetria à esquerda

9. MEDIDAS DE CURTOSE

10. Medidas de Curtose
Curtose é o grau de achatamentos de uma
distribuição em relação à distribuição padrão
(normal).

11. Medidas de Curtose
 Coeficiente (Percentílico) de Curtose
 C = Q3 – Q1 / 2 (P90 – P10)
 C < 0.263
 Distribuição Leptocúrtica
 C = 0.263
 Distribuição Mesocúrtica
 C > 0.263
 Distribuição Planticúrtica

12. Boxplot

13. Distância Interquartil
 Interquartile Range
 IQR = Q3 – Q1

14. Box Plot e a Distribuição Normal

15. Boxplot e o Gráfico de Densidade

16. EXERCÍCIO (EST007)
1. Calcular:
• Tipo de assimetria (Qualificar)
• Coeficiente de assimetria de Pearson (Qualificar)
• Coeficiente Percentílico de Curtose (Qualificar)
• Distância Interquartil (IQR)
• Desenhar boxplot
2. Adicionar os valores: 179, 186, 192, 150, 149, 151 à
amostra.
• *Todos de uma vez
• Recalcular 1 com a nova amostra

17. LINKS RECOMENDADOS
• https://www.khanacademy.org/math/cc-sixth-grade-math/cc-6th-data-statistics/cc-6th-
box-whisker-plots/v/interpreting-box-plots
• https://www.khanacademy.org/math/probability/data-distributions-a1/box--whisker-
plots-a1/v/constructing-a-box-and-whisker-plot
• https://www.khanacademy.org/math/probability/data-distributions-a1/summarizing-
spread-distributions/v/calculating-interquartile-range-iqr

18.  SOARES, J. F.; FARIAS, A. A.; CESAR, C. C.
Introdução à Estatística Básica.
 BUSSAD, W. O.; MORETTIN, P. A. Estatística
Básica.
 DEVORE, J. L. Probability and Statistics for
Engineering and the Sciences.
 CRESPO, Antônio – Estatística Fácil – 17ª ed. São
Paulo; Saraiva, 2002.
BIBLIOGRAFIA

19. Obrigado!
Dúvidas?