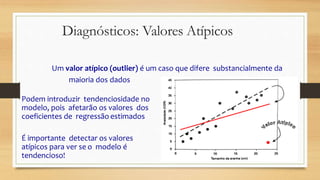
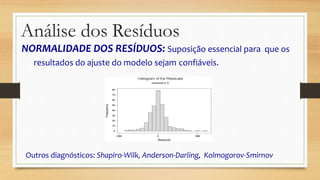
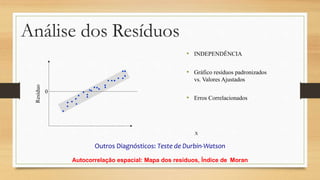
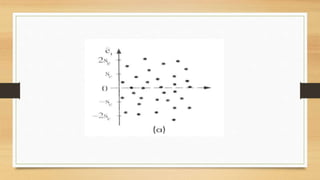
Este documento discute regressão linear, que analisa a relação entre uma variável resposta e uma ou mais variáveis preditoras. Apresenta modelos de regressão simples e múltipla, métodos de seleção de variáveis, diagnósticos de valores atípicos e pressupostos da regressão linear.

1. REGRESSÃO LINEAR

2. Análise de regressão é uma ferramenta estatística que utiliza a relação entre duas
ou mais variáveis tal que uma variável possa ser explicada (Y  variável resposta/
dependente) pela outra ou outras (X  variáveis indicadoras/ preditoras/
explicativas/ independentes).
Y = aX + b
ANÁLISE DE REGRESSÃO

3. Modelos de Regressão
Um modelo de regressão contendo somente uma variável preditora
(X) é denominado modelo de regressão simples.
Um modelo com mais de uma variável preditora (X) é
denominado modelo de regressão múltiplo.

4. Regressão Linear Simples
onde:
Yi é o valor da variável resposta na i-ésima observação;
0 e 1 são parâmetros;
Xi é uma constante conhecida; é o valor da variável preditora na i-ésima observação;
i é um termo de erro aleatório com média zero e variância constante.
Lembrando:
Saídai = (Modeloi) +erroi

5. Regressão Linear Simples

6. Yi=0+1Xi1 + 2Xi2 +…+ pXip + i
Yi é o valor da variável resposta na i-ésima observação
0, …, p são parâmetros
Xi1 ,…,Xip são os valores das variáveis preditoras na i-ésima observação
i é um termo de erro aleatório com distribuição normal, média zero e variância
constante 2 (E(i )=0 e 2 (i )= 2)
i e j são não correlacionados (independentes)para ij
Regressão Linear Múltipla

7. Superfície de Resposta:
Função de Regressão na Regressão Linear Múltipla

8. O parâmetro 0 é o intercepto do plano de regressão. Se a
abrangência do modelo inclui X1=0 e X2=0 então
0=10 representa a resposta média E(Y) neste ponto.
Em outras situações, 0 não tem qualquer outro significado
como um termo separado no modelo de regressão.
Significado dos Coeficientes de regressão:
0, 1, 2,.., p

9. Parâmetro 1 indica a mudança na resposta média E(Y) por
unidade de acréscimo em X1 quando X2 é mantido constante.
Da mesma forma, 2 indica a mudança na resposta média por
unidade de aumento em X2 quando X1 é mantido constante.
Significado dos Coeficientes de regressão:
0, 1, 2,.., p

10. Conceitualmente, a interpretação de SQTotal, SQResíduos e SQModelo permanece a mesma
SQT = SQM + SQR
Soma dos Quadrados

11. Quando existem vários previsores (X), utilizamos um
coeficiente de correlação múltiplo, denominado R Múltiplo.
R Múltiplo: É a correlação (R) entre os valores observados de Y e
os de Ŷ previstos pelo modelo de regressão múltiplo
Valores Grandes de R múltiplo  Alta correlaçãoentre os valores previstos
e observados da variável de saída.
R Múltiplo & R2

12. Resumindo: R Múltiplo é uma medida do qual bem o modelo prevê os
dados observados.
E o R2 resultante?
Pode ser interpretado da mesma forma que na regressão
simples:
É a quantidade de variação em Y que pode ser capturada pelo modelo.
R Múltiplo & R2

13. Se estamos interessados em construir um modelo complexo com vários
previsores (X1, X2, ..., Xn), como decidir qual deles considerar?
1. Avalie a importância teórica de cada variável incluída no modelo
2. Explore a relação entre Y e os previsores
3. Utilize um método de seleção dos previsores: Hierárquico (entrada em
blocos), Entrada Forçada (Enter), Métodos por passos (Stepwise)
Métodos de Regressão

14. 1. HIERÁRQUICO (ENTRADA EM BLOCOS)
Previsores selecionados com base em trabalhos anteriores. Pesquisador decide em que ordem
devem ser colocados no modelo.
2. ENTRADA FORÇADA (ENTER)
Todos os previsores são “forçados” no modelo ao mesmo tempo. Deve basear-se em
boas razões teóricas para incluir os previsores escolhidos.
Diferentemente da hierárquica, pesquisador não toma
decisões sobre a ordem em que variáveis serão acrescentadas.
Métodos de Regressão

15. 3. MÉTODOS POR PASSOS (Stepwise)
Decisão sobre a ordem em que os previsores são acrescentados ao
modelo é baseada em critérios matemáticos.
Método Forward (Para frente)
Modelo inicial contem apenas a constante (b0). Então procura-se o previsor que melhor
“prevê” a variável de saída (maior coef. de correlação) e se ele aumenta significativamente o
ajuste do modelo, ele é mantido. Procura-se então um segundo previsor e é verificada sua
capacidade de melhor significativamente o ajuste domodelo... E assim por diante.
Métodos de Regressão

16. 3. MÉTODOS POR PASSOS (Stepwise)
Decisão sobre a ordem em que os previsores são acrescentados ao
modelo é baseada em critérios matemáticos.
Método Passo a Passo (Stepwise)
Semelhante ao Forward. No entanto, cada vez que um previsor é
adicionado ao modelo, um teste de remoção é feito sobre o previsor
menos útil. Assim, a equação de regressão é acessada constantemente
para ver se algum previsor redundante pode ser removido.
Métodos de Regressão

17. 3. MÉTODOS POR PASSOS (Stepwise)
Decisão sobre a ordem em que os previsores são acrescentados ao modelo
é baseada em critérios matemáticos.
** Método Backward (Para trás) **
Oposto do método Forward (para frente). Inicia considerando todos os previsores no modelo e
vai retirando os previsores que não contribuem significativamente para o qual bem o modelo
“explica” a variável de saída (Y).
É preferível em relação ao método Forward, já que o Forward promove um maior
risco de eliminar um previsor que de fato contribui para o modelo.
Métodos de Regressão

18. Seja seletivo na inclusão de variáveis no modelo!
Priorize justificativas teóricas, baseadas em estudos
anteriores, literatura...
Como regra geral, quanto menos, melhor!!!
Métodos de Regressão

19. O quão acurado é meu modelo de regressão?
(1) O modelo representa bem os meus dados, ou ele é
influenciado por um número pequeno de casos
(valores atípicos e casos influentes)?
(2) O modelo pode ser generalizado para outras amostras?

20. (1) O modelo representa bem os meus dados, ou ele é
influenciado por um número pequeno de casos (valores
atípicos e casos influentes)?
(2) O modelo pode ser generalizado para outrasamostras?
O quão acurado é meu modelo de regressão?

21. Diagnósticos: Valores Atípicos
Um valor atípico (outlier) é um caso que difere substancialmente da
maioria dos dados
Podem introduzir tendenciosidade no
modelo, pois afetarão os valores dos
coeficientes de regressão estimados
É importante detectar os valores
atípicos para ver se o modelo é
tendencioso!

22. Diagnósticos: Valores Atípicos
RESÍDUOS: Diferença entre valores previstos pelo modelo e os valores observados na
amostra
Resíduos apresentam o erro que está presente no modelo. Modelo com bom ajuste 
Resíduos pequenos
Se qualquer caso destacar-se por ter um grande resíduo, ele poderá ser ATÍPICO
MAS COMO ESTABELECER O QUE SERIA UM “GRANDE”
RESÍDUO?

23. Diagnósticos: Valores Atípicos
Converter os resíduos (Yobservado – Yestimado) em escores-z. Ou seja,
padronizar os resíduos.
REGRAS GERAIS PARA RESÍDUOS PADRONIZADOS:
- Resíduos padronizados com valor maior do que 3,29 (3) são preocupantes porque, em uma
amostra, dificilmente acontecem por acaso
- Se mais do que 1% da nossa amostra padronizada apresenta erros maiores do que 2,58 (2,5), há
evidências de que o nível de erro dentro donosso modelo é inaceitável (modelo não se ajustabem).
- Se mais do que 5% da nossa amostra tem resíduos padronizados maiores do que 1,96 (2), também há
evidências de que nosso modelo é uma representação ruim dos dados.

24. Quando realizamos uma análise de regressão, estimamos os parâmetros de uma equação a
partir dos dados de nossa amostra.
Mas será que podemos generalizar nosso modelo, ou seja, tirar conclusões
(fazer inferências) para além da nossa amostra?
 Para generalizar um modelo de regressão, devemos estar seguros de que certas suposições foram
satisfeitas, e para testar se o modelo de fato é generalizável, podemos fazer uma validação cruzada.
 Se acharmos que nosso modelo não é generalizável, devemos restringir qualquer conclusão baseada
no modelo à amostra utilizada
Generalização

25. Pressupostos da Regressão Linear Múltipla
Os pressupostos da regressão linear simples podem ser estendidos para a regressão
linear múltipla
Existência: Para uma combinação específica das variáveis independentes X1, X2, ...,Xk,
Y é uma variável aleatória com uma certa distribuição de probabilidade, com média e
variância finitas.
Independência: As observações de Y são estatisticamente independentes umas das
outras. Este pressuposto é violado quando mais de uma observação é feita de um
mesmo indivíduo.

26. .Linearidade: O valor médio de Y para cada combinação específica de X1, X2, ...,Xk é
uma função linear de X1, X2, ...,Xk.
Ou
  componente de erro do modelo, refletindo a diferença entre o valor observado para
um indivíduo e a verdadeira resposta média
para o conjunto de indivíduos de mesmas características.
A relação entre Y e Xi é linear ou é bem aproximada por uma função linear.
Pressupostos da Regressão Linear Múltipla
XXXXXXYE kkkY XXX k
  ...)/( 2211021| 21

  kk
XXXY ...22110

27. Pressupostos da Regressão Linear Múltipla
4. Homocedasticidade: A variância de Y é a mesma para qualquer combinação fixa de X1,
X2, ...,Xk.
Este pressuposto pode parecer muito restritivo. Heterocedasticidade deve ser considerada
somente quando os dados apresentarem óbvia e significante não homogeneidade das
variâncias.
Em geral, não considerar a homocedasticidade não acarreta efeitos adversos nos resultados.
5. Amostra aleatória ou representativa da população.

28. Pressupostos da Regressão Linear Múltipla
6. Normalidade: para uma combinação fixa de X1, X2, ..., Xk, a variável
Y tem distribuição normal.
Y ~ N ( , 2)
Ou de modo equivalente
 ~N (0, 2)
 XXX k
Y 21
|

29. Pressupostos da Regressão Linear Múltipla
7. Normalidade de Y
 Este pressuposto não é necessário para o ajuste do modelo usando os mínimos quadrados, mas é
importante para a realização da inferência.
 Os testes de hipóteses paramétricos usuais e os cálculos dos intervalos de confiança utilizados nas análises
de regressão são bastante robustos, de modo que somente em casos em que a distribuição de Y se afaste muito
da distribuição normal os resultados gerados serão inadequados.
 No caso de não normalidade, transformações matemáticas de Y podem gerar conjunto de dados com
distribuição aproximadamente normal (Log Y, Y); no caso de variável Y categórica nominal ou ordinal,
métodos de regressão alternativos são necessários (logística - dados binários, Poisson - dados discretos)
 A Homocedasticidade e a Normalidade se aplicam à distribuição condicional de Y | X1, X2, ...,Xk
),(~/ 2
...,,/21 XX k21
 XYk NXXXY 

30. 1. Seleção e Preparação das Variáveis
Selecionar variáveis previsoras (X) para as quais existem razões teóricas para esperar que
prevejam bem o resultado.
Diagramas de Dispersão e Matriz de Correlações
Verificar as correlações entre variáveis: As variáveis X devem ser correlacionadas com Y, mas
não entre si  primeira análise de multicolinearidade
Verificar se as relações entre X e Y são lineares  Transformações podem ser necessárias para
linearizar relações.
Etapas da Análise de Regressão

31. 1. Seleção e Preparação das Variáveis
2. Escolha e Ajuste do Modelo de Regressão
 Uma estratégia seria executar a regressão para todos os previsores (X) selecionados e
examinar a saída para ver quais contribuem substancialmente para o modelo.
 Uma vez determinada quais são as variáveis importantes, execute novamente a análise
incluindo somente essas variáveis e utilize as estimativas dos parâmetros resultantes para
definir o modelo de regressão.
Etapas da Análise de Regressão

32. 1. Seleção e Preparação das Variáveis
2. Escolha e Ajuste do Modelo de Regressão
3. Diagnóstico para verificar se o modelo ajustado é adequado
 Ajuste do modelo (R2, Teste F, Testes t para coef.)
 Multicolinearidade (FIV)
 Análise dos Resíduos
Etapas da Análise de Regressão

33. Se modelo for adequado, resíduos devem refletir as propriedades
impostas pelo termo de erro do modelo.
LINEARIDADE DO MODELO
Análise dos Resíduos

34. NORMALIDADE DOS RESÍDUOS: Suposição essencial para que os
resultados do ajuste do modelo sejam confiáveis.
Outros diagnósticos: Shapiro-Wilk, Anderson-Darling, Kolmogorov-Smirnov
Análise dos Resíduos

35. Outros diagnósticos:
Teste de Breush-Pagan.
Análise dos Resíduos

36. PRESENÇA DE OUTLIERS
Gráfico resíduos padronizados vs. Valores Ajustados
Pontos Influentes: DFFITS, DFBETA, Distância de Cook.
Análise dos Resíduos

37. • INDEPENDÊNCIA
• Gráfico resíduos padronizados
vs. Valores Ajustados
• Erros Correlacionados
X
Outros Diagnósticos: Teste de Durbin-Watson
Autocorrelação espacial: Mapa dos resíduos, Índice de Moran
Análise dos Resíduos

38. Quais dessas plotagens mostram normalidade dos resíduos? Quais os
problemas das outras?
Análise dos Resíduos

40. Design de Experimentos

41. Tipos de Design de Experimentos
• Um único fator
• Vários fatores
• Experimentos fatoriais com 2 fatores;
• Experimentos fatoriais 2^k

42. Experimentos Fatoriais 2k
• Experimentos com k fatores e cada fator tem apenas dois níveis
• Caso especial dos experimentos fatoriais com k fatores
• Os fatores podem ser:
a) Quantitativos: dois valores de temperatura, pressão ou tempo
b) Qualitativos: níveis “alto” e “baixo”, presença e ausência de um fator, duas máquinas, dois
operadores, gênero
• Um replicação completa requer:
2 x 2 x 2 x … x 2 = 2k observações

43. Experimentos Fatoriais 2k
• Os fatoriais 2k são muito úteis no primeiros estágios da experimentação,
quando muitos fatores podem ser de interesse (screening)
• Permite testar k fatores num fatorial completo com o menor número de
rodadas
• Assume-se que a resposta é aproximadamente linear entre os dois níveis
• Continuaremos assumindo que:
1. os fatores são fixos
2. o experimento é completamente aleatorizado
3. as suposições de normalidade são satisfeitas

44. Experimentos Fatoriais 22
• Caso mais simples do experimentos fatoriais 2k
• Temos dois fatores (k=2) com 2 níveis cada
• Cada replicação completa do experimento requer 22=4
observações, ou seja, 4 tratamentos
• Os níveis dos fatores são denominados: baixo (−) e alto (+)
Fator Representação
A B Tratamento do Tratamento Observação
− − A−B−
(1) y11k
+ − A+B−
a y21k
− + A−B+
b y12k
+ + A+B+
ab y22k

45. Fatoriais 22 - Representação Geométrica
• Os quatro tratamentos podem ser representados da seguinte forma:
Fator
A B Tratamento
− − (1)
+ − a
− + b
+ + ab

46. Fatoriais 22 - Exemplo
• Pipoca de Microondas
• Problema: grãos que sobram sem estourar

47. Exemplo – Pipoca no Microondas
• Possíveis fatores que influenciam na quantidade de grãos
que sobra sem estourar
1. Marca da pipoca
2. Tempo no microondas
3. Potência
4. …
• Vamos selecionar dois fatores com dois níveis cada:
Marca da pipoca (1 e 2)
Tempo no microondas (4 e 6 minutos)
• Variável resposta: peso (g) dos grãos sem estourar
• Repetiremos o experimento 3 vezes (replicação)

48. Exemplo – Pipoca
• Existem 4 tratamentos e 3 replicações, resultando num total de 12
observações
• As 12 rodadas foram executadas em ordem completamente aleatória
• Os dados estão na tabela abaixo
Fator Replicação
Marca
(A)
Tempo
(B)
Tratamento I II III Total
− − (1) 28 25 27 80
+ − a 36 32 32 100
− + b 18 19 23 60
+ + ab 31 30 29 90

49. Exemplo – Pipoca
• O modelo linear para esse experimento ainda pode ser escrito da forma
usual:
• E as SS podem ser calculadas como antes
• No entanto, veremos um maneira alternativa de calcular as SS para esse
tipo particular de modelo
• Na notação usada aqui, letras maiúsculas denotam os fatores (A e B) e as
letras minúsculas denotam os tratamentos (a, b, ab)

50. Efeitos Principais e Interação
• No desenho fatorial 22 podemos definir o efeito médio de um fator como a
mudança na resposta produzido pela mudança no nível do fator, tirando a média
sobre os outros níveis do outro fator.
• O efeito de A no nível baixo de B é
• O efeito de A no nível alto de B é
• O efeito médio da interação AB é a diferença média entre o efeito de A no nível
alto de B e o efeito de A no nível baixo de B
[a -(1)]
n
[ab- b]
n

51. Efeitos Principais e Interação
• Efeitos principais
• Interação

52. • Efeitos principais
Efeitos Principais e Interação
• Interação

53. Exemplo - Pipoca
• Calculamos os efeitos principais e a interação no
exemplo da pipoca
• Examinar a magnitude e direção dos efeitos para
determinar quais variáveis são importantes

54. Exemplo - Pipoca
• Calculamos os efeitos principais e a interação no exemplo da pipoca
• A = 8.33, B = -5, AB = 1.67
• O efeito de A é positivo: aumentar A de “baixo” para “alto” aumenta
o peso dos grãos sem estourar
• O contrário para B
• A interação parece ser pequena em relação aos efeitos principais

55. Exemplo – Pipoca
• Tabela ANOVA:
• Ambos efeitos principais (marca da pipoca e tempo no microondas) são significantes,
isto é, influenciam na quantidade de grãos que ficam sem estourar
• E a interação?

56. Exemplo – Pipoca
• Interação AB não é significante

57. Regressão
• Em um experimento fatorial 22, é fácil expressar os resultados em um
modelo de regressão
• Para o exemplo da pipoca temos
• Onde x1 é representa o fator 1, assumindo -1 ou 1
e x2 representa o fator 2, também assumindo -1 ou 1
y = b0 +b1x1 +b2x2 +e

58. Regressão
Lembrando que
A = Marca da pipoca (1 e 2)
B = Tempo no microondas (4 e 6 minutos)
x1 =
Marca-(Marcabaixo + Marcaalto ) / 2
(Marcaalto - Marcabaixo )/ 2
x2 =
Tempo-(Tempobaixo +Tempoalto )/ 2
(Tempoalto -Tempobaixo )/ 2
x1 =
Marca-(1+2)/ 2
(2-1)/ 2
x2 =
Tempo-(4+6) / 2
(6- 4) / 2

59. Regressão
• A regressão ajustada é então
• Onde o intercepto é a média geral
y = 27.5+
8.33
2
æ
è
ç
ö
ø
÷x1 +
-5
2
æ
è
ç
ö
ø
÷x2

60. Fatoriais 23
• Experimentos com 3 fatores e 2 níveis cada
2 x 2 x 2 = 23 = 8 tratamentos
• Representação geométrica

61. Fatoriais 23
• Tabela dos sinais para calcular os efeitos
Efeito Fatorial
Tratamento I A B AB C AC BC ABC
(1) + − − + − + + −
a + + − − − − + +
b + − + − − + − +
ab + + + + − − − −
c + − − + + − − +
ac + + − − + + − −
bc + − + − + − + −
abc + + + + + + + +