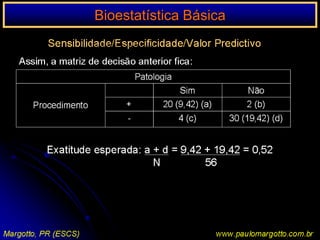
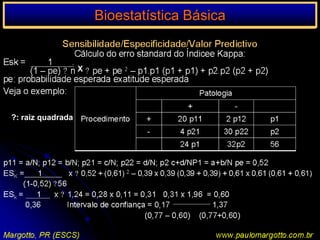
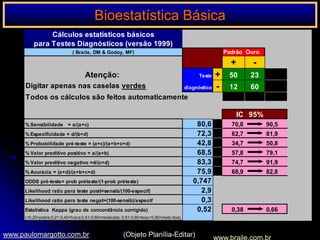
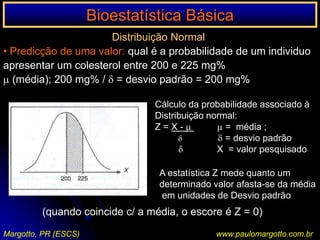
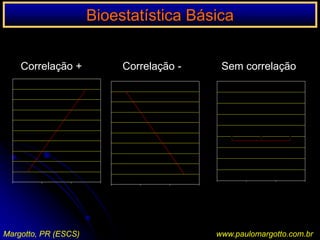
Bioestatistica basica completa-apresentacao

Bioestatística Básica Secretaria de Estado de Saúde do Distrito Federal Fundação de Ensino e Pesquisa em Ciências da Saúde (FPECS)Escola Superior de Ciências da Saúde (ESCS)Paulo Roberto MargottoProf. Do Curso de Medicina da ESCSwww.paulomargotto.com.br

Bioestatística Básica Programa:Importância da Bioestatística Variáveis População e Amostras Apresentação dos dados em tabelas Medidas de Tendência CentralDistribuição Normal Correlação e Regressão Risco Relativo / Odds Ratio Teste de Hipóteses Exercício de Medicina Baseado em Evidências Teste de Fisher Teste t Estadígrafo de Sandler Análise de Variância (ANOVA) Escolha de Teste Estatístico Testes Estatísticos não Paramétricos Sensibilidades/Especificidade Margotto, PR (ESCS)

Bioestatística Básica Todos confortavelmente acomodados !?BOA SORTE !!!!Margotto, PR (ESCS)

Bioestatística Básica Depende, em boa parte, do conhecimento sobre BioestatísticaA condução e avaliação de uma pesquisa

Comparação entre dois ou mais grupos ou amostras (grupo tratado / grupo controle)Avaliação da eficácia do tratamento (significação)Estar alerta a: variáveis interferentes nos resultados¤ Variações mostrais¤ Diferenças entre gruposMargotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaOs testes estatísticos são utilizados para:¤ Comparar amostras(houve modificação dos grupos inicialmentesemelhantes após o início da intervenção)¤ Detectar variáveis interferentes¤ Analisar se o tratamento depende de outras variáveis (peso, idade, sexo)Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaA ciência não é um conhecimento definitivo sobre a realidade, mas é um conhecimento hipotético que pode ser questionado e corrigido.Ensinar ciências não significa apenas descrever fatos, anunciar leis e apresentar novas descobertas, masEnsinar o método científico Maneira crítica e racional de buscar conhecimentoVieira S., 1991.Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaVariáveis (dados):

Qualitativos ou nominais: sexo, cor, grupo sanguíneo, causa da morte

Ordinais: (ordenação natural): Grau de instrução, aparência, estágio da doença, status social

Quantitativos ou Contínuos: (dados expressos por nº): idade, altura, peso

População: Conj. de elementos com determinada característica

Amostra:Subconjunto com menor nº de elementos

Independentes: grupo selecionados com tratamento distinto

Dependentes: para cada elemento do grupo tratado existe um grupo controle semelhante (sexo, idade, etc)

Comparação intra-individuo (o grupo submetido ao tratamento é o seu próprio controle)Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaApresentação dos Dados em Tabelas:

Corpo: Formado pelas linhas e colunas dos dados

Cabeçalho: específica o conteúdo das colunas

Coluna indicadora: específica o conteúdo das linhas

Opcional: fonte, notas, chamadasMargotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística Básica Nascidos vivos no Maternidade do HRAS segundo o ano de registro TítuloCabeçalho (separado do corpo por um traço horizontal)Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaTabela de Contingência ou de Dupla Entrada(cada entrada é relativa a um dos fatores)Gestantes sem pré-natal/gestantes com pré-natal e mortalidade perinatalMargotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaTabelas de distribuição de freqüências:Peso ao nascer de nascidos vivos, em KgMenor peso: 1570gMaior peso: 4600gComo transformar está tabela em uma Tabela de Distribuição de Freqüência ?Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaTabelas de distribuição de freqüências: 3 colunasDefinir as faixas de peso (Classes): Intervalo de classe (0,5Kg): intervalo coberto pela classe

Extremo de classe:limites dos intervalos de classe 1,5 Ι— 2,0: fechado a esquerda (não pertencem a classe os Valores  2; pertencem a classe os valores  1,5)- Ponto médio: soma dos extremos da classe ÷ 2N º de classes: K = 1+ 3,222 log n (em geral: 5-20) no exemplo: K = 1 + 3,222 log 100 = 7,444 (7 ou 8 classes)Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaMedidas de Tendência Central(Valor de ponto em torno do qual os dados se distribuem)Variância e Desvio Padrão: avalia o grau de dispersão quanto cada dado se desvia em relação a média)Média aritmética:soma dos dados  nº deles(dá a abscissa do centro de gravidade do conjunto de dados)A média aritmética (representa-se por X é: 2,5+3,0+3,5+ ... 4,0 = 2,45 10Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaMedidas de Tendência CentralMédia AritméticaCálculo da média de dados em Tabela de Distribuição de Frequêncian=100 Média (X): ponto médio de cada classe x respectiva freqüência divido pelo nX = 1,75x3 + 2,25x16 + ... 4,25x4 + 4,75x1 = 300 3 Kg 100 100Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaMedida de Tendência CentralMedida de dispersão:indicadores do grau de variabilidade dos individuos em torno das medidas de tendência central

Medir os desvios em relação a média(diferença de cada dado e a média)Não há média dos desvios pois sua soma é igual a zeroEx.: 0,4,6,8,7X (média) : 0+4+6+8+7 = 25 = 5 5 5X – X (desvio em relação a média) 0 - 5 = - 5 4 – 5 = -1 A soma dos desvios é igual a zero 6 – 5 = 1 8 – 5 = 3 (-5 + -1)+1+3+2= - 6 + 6 = 0 7 – 5 = 2Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaMedidas de Tendência CentralVariânciaSoma dos quadrados dos desviosA soma do quadrado dos desvios não é usada como medida de dispersão, porque o seu valor cresce com o nº de dados Grupo I: 60, 70 e 80 Kg - Grupo II: 60, 60, 70, 70, 80, 80 KgMargotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaMedidas de Tendência CentralVariânciaCálculo da soma dos quadrados dos desviosEntão, para medir a dispersão dos dados em relação à média, usa-se a variância (S2) que leva em consideração o nS2 = soma dos quadrados dos desviosn – 1Para os dados: 0, 4, 6, 8 e 7 a S2 = 40 = 40 = 10 5 –1 4Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística Básica IMedidas de Tendência CentralDesvio PadrãoRaiz quadrada da variância, sendo representava por S; tem a mesma unidade de medida dos dadosEx.: 0,4,6,8,7. S2 (variância) = 10 s (desvio padrão): √10 = 3,16Coeficiente de variância (CV) Razão entre o desvio padrão a a média x 100CV = 6 x 100XEx.: Grupo I: 3,1,5 anos (x = 3 anos; s2 = 4; s=2) : CV = 66,7% Grupo II: 55,57,53 anos (x = 55 anos; s2 = 4; s = 2) : CV = 3,64%Vejam à dispersão dos dados em ambos os grupos é a mesma, mas os CV são diferentes (no grupo I a dispersão relativa é ALTA) Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaDistribuição Normal Variáveis aleatórias: variam ao acaso (peso ao nascer)

Gráficos com 2 extremos um máximo e um mínimo e entre eles, uma distribuição gradativa (maioria dos valores ao redor da média) : Curva de Gauss: As medidas que originam a estesgráficos são variáveis com distribuição normalMargotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaDistribuição Normal Características:

A variável (peso ao nascer) pode assumir qualquer valor real

O Gráfico da distribuição normal é uma curva em forma de sino, simétrico em torno da média () (se lê “mi”).

A área total da curva vale 1, significando que a probabilidade de ocorrer qualquer valor real é 1.

Pelo fato da curva ser simétrica em torno da média, os valores maiores do que a média e os valores menores do que a média ocorrem com igual probabilidade.Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaDistribuição NormalPredicção de uma valor entre dois nº quaisquer:Ex.: A probabilidade de ocorrência de um valor > 0 é 0,5, mas qual é a probabilidade de ocorrer um valor entre 0 e z = 1,25?Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaDistribuição NormalPredicção de uma valor Usar tabela de Distribuição NormalComo usar esta tabela?Localizar na 1a coluna o valor 1,2 Na 1a linha, está o valor 5.n0 1,2 compõe com o algarismo 5, o n0 z = 1,25.No cruzamento da linha 1,2 com a coluna 5 está o número 0,3944. Está é a probabilidade (39,44%) do ocorrer valor entre zero e z= 1,25.Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaProbabilidade de ocorrer valor entre zero e 1,25Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaDistribuição Normal Predicção de uma valor: qual é a probabilidade de um individuo apresentar um colesterol entre 200 e 225 mg% (média); 200 mg% /  = desvio padrão = 200 mg%Cálculo da probabilidade associado à Distribuição normal:Z = X -  = média ; = desvio padrão  X = valor pesquisado A estatística Z mede quanto um determinado valor afasta-se da média em unidades de Desvio padrão(quando coincide c/ a média, o escore é Z = 0)Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaDistribuição Normal Predicção de uma valor:Z = X – 200 = 1,25 20Consultando a Tabela de Distribuição normal, vemos que a probabilidade de Z assumir valor entre 0 e Z = 1,25 é 0,3944 ou 39,44Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaDistribuição Normal Predicção de uma valorOutro exemplo: Qual é a probabilidade uma pessoa apresentar menos do que 190mg% de colesterol. Para resolver este problema, é preciso "reduzir" o valor X = 190.Obtém-se então: Z = 190 - 200 = - 0,50 . 20Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaNa Tabela de Distribuição Normal, a probabilidade de ocorrer valor maior que a média 0 é 0,5;então, a probabilidade pedida é : 0,5 – 0,1915 = 0,3085 ou 38,85%Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaCorrelação / RegressãoCorrelaçãoAssociaçao entre duas variaveis peso e altura; em quanto aumenta o peso à medida que aumenta a altura? Diagrama de dispersão:

X = Horizontal (eixo das abscissas): variável independente ou explanatória

Y = Vertical (eixo das ordenadas) : variável dependenteA correlação quantifica quão bem o X e Y variam em conjuntoMargotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaCorrelação + Correlação - Sem correlaçãoMargotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaCorrelação / RegressãoObservem que à medida que o comprimento dos cães aumenta (variável explanatória) o peso aumenta (variável dependente)Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaCorrelação / Regressão Coeficiente de correlação: (r de Pearson) :Expressa quantitativamente as relações entre duas variáveisr = 0,8 – 1 – forter = 0,5 – 0,8 – moderadaR = 0,2 – 0,5 – fracar = 0 – 0,2 – insignificanteCálculo do r:r = ∑xy - ∑x∑y n 000000000∑x2 – (∑x)2 n∑y2 – (∑y)2 nMargotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaCorrelação / Regressão Correlação: grau de associação / Regressão: capacidade entre 2 variáveis de predicção de um valor baseado no conhecimento do outro(prever Y conhecendo-se o X)Equação da Reta de Regressão:Y = a + bx (a= Y – bx)a : coeficiente angular (inclinação da reta)b: coeficiente linear (intersecção da reta com o eixo X)Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaCorrelação / Regressão Exemplo: a correlação entre o peso pré-gravídico e o peso do RN foi de 0,22. Aequação da reta: Y = 2547, 79 + 12,8 x Assim, uma gestante com peso pré-gravídico de 60 Kg espera-se um RN c/ peso de 3,315gR2 ( r squared): coeficiente de determinação: proporção da variação total que é explicada. Peso pré –gravídico e peso ao nascer : r2 = 0,22 2 = 4,84 ≈ 5%( o peso ao nascer é explicado pelo peso da mãe em apenas 5%)(Tese de Doutorado – Curvas de Crescimento Intra-uterinas Margotto, PR)Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaCorrelação / Regressão Para testar o valor de coeficiente de correlação linear, podemos empregar o teste t, aplicando a fórmula:t = r x √n – 2 graus de liberdade : n - 2 √1 – r 2Se t > tc, conclui-se que o r é significativoMargotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaCorrelação / Regressão Base excess e Pa CO2Equação de regressão: Y = 1,07 BE + 40 ,98 r = 0,94 / r = 0.88 = 88%Grafico tirado do livro cápitulo distri eq acido basicoMargotto, PR (ESCS)www.paulomargotto.com.br

INTERPRETAÇÃO DO RISCO RELATIVO/ODDSRATIO EM PERINATOLOGIA/TESTE DE HIPÓTESES272310280302582Taxa de eventos no grupo estudo: (a/(a+b)Taxa de eventos no grupo controle: (c/(c=d)Risco relativo: a/(a+b) / c(c+d)Redução do risco relativo (RRR)Redução do risco absolutoNúmero Necessário p/tratamentowww.paulomargotto.com.br(Objeto Planilia-Editar)www.braile.com.br

INTERPRETAÇÃO DO RISCO RELATIVO/ODDSRATIO EM PERINATOLOGIA/TESTE DE HIPÓTESESO Intervalo de Confiança 95% significa que há 95% de probabilidade de que o intervalo calculado contenha o verdadeiro valor do parâmetro estudado. Por exemplo RISCO RELATIVO de 1,6 com IC95% de 1,2 a 2,05. Isto quer dizer que no experimento realizado o valor encontrado foi de 1,6 e que há 95% de probabilidade que o verdadeiro valor seja um número qualquer entre 1,2 E 2,05. Quando o intervalo de confiança contém o valor 1,00 significa que não há diferença estatística entre o grupo estudado e o grupo controle. 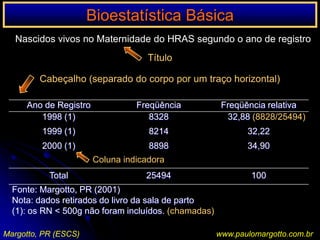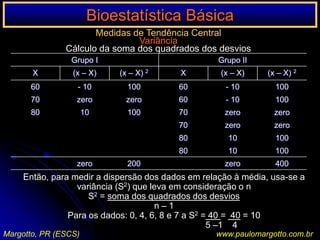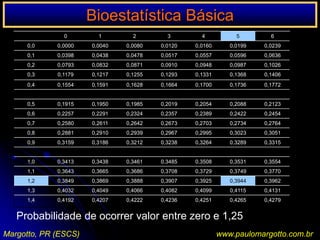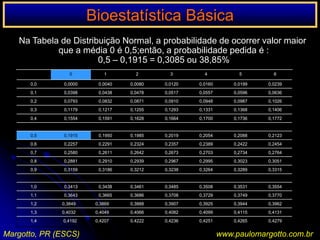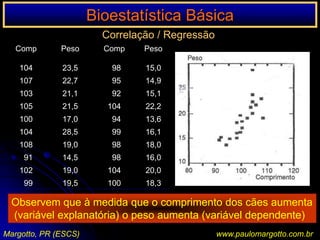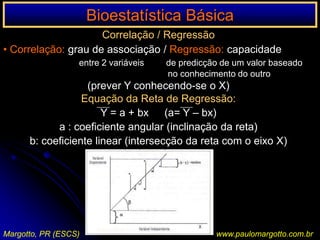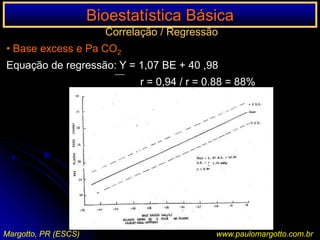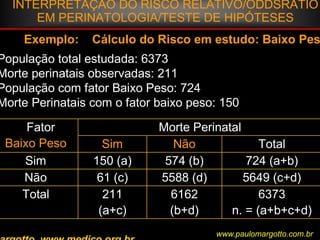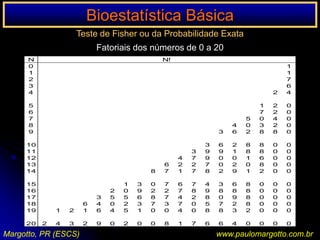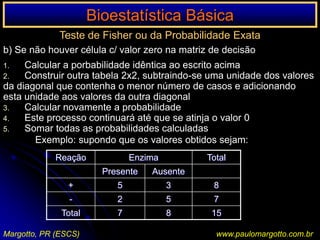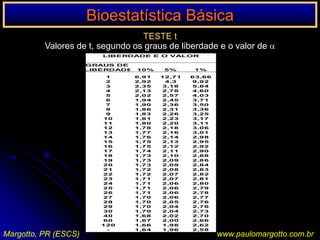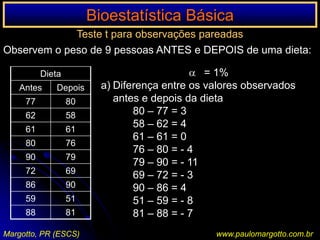Quando o valor máximo do IC95% é menor que 1,00 o grupo de estudo se comportou de modo significativamente melhor que o grupo de controle e quando o valor mínimo do IC95% for maior que 1,00 significa que o grupo de estudo foi significativamente pior que o grupo controle.www.braile.com.brwww.paulomargotto.com.br

INTERPRETAÇÃO DO RISCO RELATIVO/ODDSRATIO EM PERINATOLOGIA/TESTE DE HIPÓTESESwww.braile.com.brwww.paulomargotto.com.br

INTERPRETAÇÃO DO RISCO RELATIVO/ODDSRATIO EM PERINATOLOGIA/TESTE DE HIPÓTESES(Cálculos usando o Programa DPP Braile Biomédica)EstudoControlewww.paulomargotto.com.br(Objeto Planília-Editar)www.braile.com.br

Bioestatística BásicaTeste de HipóteseHipótese nula (H0): não há diferença

Hipótese alternativa (H1): há diferençaHipótese: resposta presumida e provisória que de acordo com critério será ou não rejeitadaProcesso para testar hipótese:1. Estabelecer Ho2. Estabelecer H13. Determinar tamanho da amostra4. Colher dados5. Estudo estabelecido para verificar se o H0 é verdadeiro6. Rejeitar ou não a H0Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaTeste de HipóteseSegundo R.A. Fisher: todo experimento existe somente com o propósito de dar os fatos uma oportinidade de afastar a H0

Erro tipo I: rejeitar a H0 sendo verdadeira (fato obtido pelo azar) :rara ocorrência estatística; amostras pequenasErro tipo II: aceita a H0 sendo falsa (erro mais frequente);significação estatística: máxima probabilidade de tolerar um erro tipo I.α= 5% (p 0,05): ≤ 5% de rejeitar a H0 (sendo verdadeira) e aceitar a H1α= 1% (p 0,01): ≤ 1% de rejeitar a H0 (sendo verdadeira) e aceitar a H1α erro tipo I e erro tipo IIα erro tipo I e erro tipo II ‘Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaExercício da Medicina Baseado em Evidências (MBE)Novo paradigma na prática clínica: decisões com evidência da pesquisa clínica

MBE – uso consciencioso da melhor evidência na tomada de decisões integrado com a experiência Sem experiência clínica – as práticas correm o risco de ser tiranizadas pela evidênciaEstratégia poderosa: busca eletrônica -www.pubmed.com -www.cochrane.org: compêncio de reevisões sistemáticas dos estudos randomizados de todos os campos da medicina(Na medicina neonatal: www.nichd.nih.gov/cohrane) -www.bireme.br -www.paulomargotto.com.br -www.neonatology.org Margotto, PR (ESCS)

Bioestatística BásicaMREConhecimento da Estrutura de um estudo da Avaliação de um tratamento:Exposição Medidas do efeito de tratamento:RR (Risco Relativo): a/n1 c/n2RRR (redução do Risco Relativo): 1 – RRDR (Diferença de Risco): a/n1 – c/n2Número necessário para tratamento (NNT): 1 Diferença de riscoMargotto, PR (ESCS)www.paulomargotto.com.br

INTERPRETAÇÃO DO RISCO RELATIVO/ODDSRATIO EM PERINATOLOGIA/TESTE DE HIPÓTESES272310280302582Taxa de eventos no grupo estudo: (a/(a+b)Taxa de eventos no grupo controle: (c/(c=d)Risco relativo: a/(a+b) / c(c+d)Redução do risco relativo (RRR)Redução do risco absolutoNúmero Necessário p/tratamentowww.paulomargotto.com.brObjeto Planília-Editarwww.braile.com.br

Bioestatística BásicaMRERR = 1 (sem efeito no tratamento)RR < 1 ( o risco de evento é menor no grupo tratado)Ex.: Redução do DAP (ductus arteriosus patente) no grupo exposto a menor ou maior oferta hídricaRR = 0,40 (IC 95% : 0,26 – 0,63): não contém 1 (é significativo)RRR = 1 – RR = 1 – 0,40 = 0,60 x 100 = 60 % (redução de 60% do DAP no grupo com menor oferta hídrica)DR: - 0,19NNT = 5,3 ( o nº necessário para tratar com restrição hídrica para prevenir um caso de DAP é 5,3 Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaMREHemorragia peri/intraventricular (HP/HIV): grupo com menor x maior oferta hídrica:RR = 0,94 (IC a 95% : 0,52 – 1,72)RRR = 1 – 0,94 = 0,06 x100 = 6% DR = - 0,011 NNT = 90,9Interpretação: A ingesta hídrica não afetou a incidência de HP/HIV (no intervalo de confiança do RR contém o 1, que quando presente significa nulidade da associação)

A restrição hídrica diminui a HP/HIV (não significativo)

É necessário restringir líquido em 90,9 RN para evitar a ocorrência de 1 caso de HP/HIVQuanto melhor o tratamento, menor o NNTMargotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaMREUso da dexametasona no tratamento da Displasia broncopulmonar (DBP) e efeito colateral Hiperglicemia : RR = 1,27 (IC a 95%: 0,99 – 1,63). Há um aumento da glicemia em 27% dos pacientes (1,25 x 100 = 127: 100 + 27). Não significativo, pois o IC contem a unidade Hipertrofia do miocárdio: RR = 9,0 (IC a 95%: 1,2 – 67,69).Aumento significativo de 9 vezes (o intervalo não contém a unidade)Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaMREA apresentação dos Dados: Vejam a apresentação dos resultados: RR (95% IC)Ingesta hídrica menor x maiorDuctus arteriosus patenteHemorragia peri/intraventricularEfeitos colaterais do uso da dexametasona na DBPHiperglicemiaHipertrofia do miocárdioQuando a linha horizontal estiver a esquerda (RR<1) redução do evento; quando à direita (RR> 1): aumento do evento Toda vez que a linha horizontal tocar a linha vertical significa qu o RR não é significativo11Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaMRE- Comparação do lucinactante (Surfaxin ®) x Colfosceril (Exosurf ® ) Comparação do lucinactante (Surfaxin ®) x Beractante (Survanta ® )Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaMREOR (Odds ratio): é uma estimativa do risco relativo(Razão de chances) mesma interpretação do RR Antigo paradigma da prática clínica:

Tomada de decisões se baseavam em:

Bastante conhecimento de fisiopatologia

Opinião de especialistas (professores)

Novo paradigma da prática clínica

Tomada de decisões se baseiam em :

Evidências das pesquisas clínicas, evidentemente com embasamento na experiênca clínicaMargotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaTeste de Fisher ou da Probabilidade ExataUsado para amostras pequenas

Menos erro tipo I e II em relação ao qui-quadrado

n < 20 / n > 20 < 40Ex.: a) célula da matriz de decisão com o valor 0Suposição de uma determinada enzima em pessoas submetidas a uma reação sorológicaP = (a+b!) x (C=d!) x (a+c!) x (b+d!) n! x 1 / a! b! c! d!P = [ (6! 3! 5! 4! / 9!] x [1/5! 1! 0! 3!)P = 0,046 = 4,76%P < 5%: as pessoas submetidas a uma reação sorológica apresentam significativamente uma determinada enzima (afastamos a H0)Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaTeste de Fisher ou da Probabilidade ExataFatoriais dos números de 0 a 20Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaTeste de Fisher ou da Probabilidade Exatab) Se não houver célula c/ valor zero na matriz de decisãoCalcular a porbabilidade idêntica ao escrito acimaConstruir outra tabela 2x2, subtraindo-se uma unidade dos valoresda diagonal que contenha o menor número de casos e adicionandoesta unidade aos valores da outra diagonalCalcular novamente a probabilidadeEste processo continuará até que se atinja o valor 0Somar todas as probabilidades calculadas Exemplo: supondo que os valores obtidos sejam:Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaTeste de Fisher ou da Probabilidade ExataCalculariamos:P = (8! 7! 7! 8!/15) )1/5! 3! 2! 5!)P = 0,1828P = (8! 7! 7! 8!/15) )1/6! 3! 2! 6!)P = 0,0305P = (8! 7! 7! 8!/15) )1/0! 7! 1! 7!)P = 0,0012p = 0,1828 + 0,0305 + 0,0012 = 0,2145 = 21,45% p> 5%: as pessoas submetidas a reação sorológica NÃO apresentam significativamente determinada enzima (aceitamos a H0)Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaTeste tTestar o QI médio entre crianças nascidas a termo e prematuras

Testar uma droga (grupo tratado/grupo controle)

Teste t: analisa grupos simples ou compara 2 grupos(variável com distribuição normal ou aproximadamente normal)Passos:Nível de significância: letra grega 

Média de cada grupo: X1: média do grupo 1 X2: média do grupo 2Variância de cada grupo: S21: variância do grupo 1 S22: variância do grupo 2N1 é o nº de elementos do grupo 1 N2 é o nº de elementos do grupo 2 Variância PonderadaS2 = (n1 – 1)2 + (n2 – 1) S22 n1 + n2 - 2O valor t é definido pela fórmulat = X 2 – X1 1 1√ S2 n1 + n2Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaTeste tt0 (t calculado)  tc (t crítico: obtido na tabela de valores de t)Significa que as médias não são iguais, podendo se afastar a H0Ex.: 1) Verificar se duas dietas para emagrecer são igualmente eficientes ou se determinada dieta foi melhor (produziu significativamente menor perda de peso) Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaPerda de peso em Kg segundo a dietaInicialmente, vamos estabelecer o nível de Significância: = 5%Cálculos: Média de cada grupoX1 = 12 + 8 + ... + 13 = 120 = 12 10 10 X2 = 15 + 19+ ... 15 = 105 = 15 7 7 Variância de cada grupo:S12 = 4 S22 = 5Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaTESTE tVerificação de duas dietas (continuação)Variância ponderada:S22 = 9x4 + 6x5 = 4,49+6Cálculo do valor de t:t= 15 – 12 = 2,902√ 4,4 1 + 1 10 7Graus de liberdade: n1 + n2 – 2 = 10 +7 – 2 = 15(Correção em função do tamanho da amostra e do nº de combinações possíveis)Na tabela de valores de t : t0 > tc: a dieta 2 produziu maior perda de peso (significativo):rejeitamos a H0Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaTESTE tValores de t, segundo os graus de liberdade e o valor de Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaTESTE tQuando as variâncias são desiguais; a fórmula do teste t é:X2 – X1t = S21 + S22√n1 n2O número de graus de liberdade é o nº inteiro mais próximo do g obitido pela fórmula:Para saber se as variâncias são iguais: se a maiorvariância for 4 vezes menor, admite-se que as duas populações têm variâncias iguaisEx.: S21 = 15,64; S22 = 6,80 15,64 < 4 (as variâncias 6,8 são iguais) S21+ S222n1 n2g =S21 2+ S222n1+ n2 n1 - 1 n2 - 1Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaTESTE tEx.: Um médico aplicou uma dieta a um grupo de pacientes e o outro (controle) continuou com os mesmos hábitos alimentares. Houve maior perda de peso com a dieta ?Nível de significância estabelecido: = 5%média de cada grupo: X1 = 12 X2 = 0,5 variância de cada grupo: S21 = 5,0 S22 = 0,23Para saber se as variâncias são ou não iguais: S21 5 S22 = 0,25 = 20 ( 4 – são desiguais )Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaTESTE tAvaliação de um grupo com dieta e outro não para emagrecimento:Continuação:Cálculo do t com variâncias desiguais: t = 0,5 – 12 t = 11,5 = 13,28√5,0 + 0,25√5,25 7 7 7O nº de graus de liberdade:5,0 + 0,2527 7g = 5,0 2+ 0,2527 7 6 + 6g = 0,5625 = 6,6  7 graus de liberdade 0,085247t0 > tc: rejeitamos a H0 de que as médias são iguais ou seja,a perda de peso é significativamente maior no grupo com a dietaMargotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaTeste t para observações pareadasÀs vezes os pesquisadores estudam os efeitos de um tratamentocomparando-se:* Pares de individuos ( um gêmeo recebe um tratamento e o outro, não). * Dois lados de um mesmo individuo (aplicação de um tratamento para aprevenção de cáries em um lado da arcada dentária eo outro lado semtratamento – controle).Como fazer o teste t:Nível de siginificância ()

Diferença entre as unidades de cada um dos n pares d = X2 – X1

Média das diferenças d = d (d:somatória das diferenças) nVariância das diferenças: S2 = d2 - (d)2 n n – 1O valor de t: t = dS2nGrau de Liberdade: n – 1 Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatística BásicaTeste t para observações pareadasObservem o peso de 9 pessoas ANTES e DEPOIS de uma dieta: = 1% Diferença entre os valores observados antes e depois da dieta 80 – 77 = 3 58 – 62 = 4 61 – 61 = 0 76 – 80 = - 4 79 – 90 = - 11 69 – 72 = - 3 90 – 86 = 4 51 – 59 = - 8 81 – 88 = - 7Margotto, PR (ESCS)www.paulomargotto.com.br

Bioestatistica basica completa-apresentacao

Mais conteúdo relacionado

Mais procurados

Destaque

Semelhante a Bioestatistica basica completa-apresentacao

Mais de Fabiano Reis

Último

Bioestatistica basica completa-apresentacao