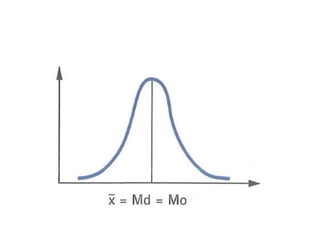
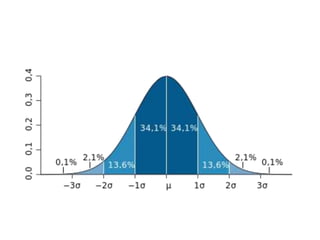
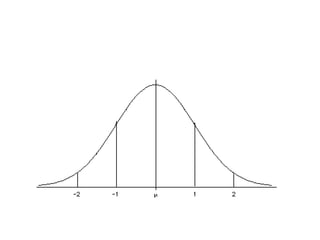
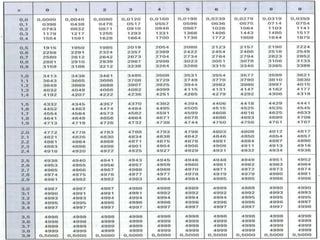
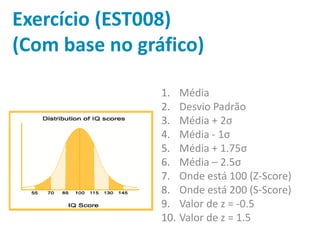
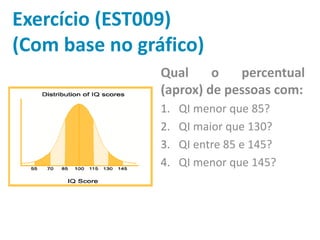
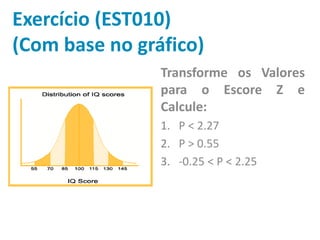
Este documento discute estatística descritiva, incluindo distribuição normal, escore z, probabilidade z e exemplos. Eventos próximos à média são mais comuns do que eventos extremos na distribuição normal. O escore z mede o quão distante um valor está da média em termos de desvios padrão. A probabilidade z calcula a probabilidade de um valor estar abaixo ou acima de um determinado escore z.

1. ESTATÍSTICA DESCRITIVA
Ranilson Paiva
Ranilson Paiva ranilsonpaiva@ic.ufal.br
A DISTRIBUIÇÃO NORMAL

2. A DISTRIBUIÇÃO NORMAL

3. Eventos extremos são pouco
comuns.
Eventos próximos a um valor
de referência (média), são
mais comuns.

6. ESCORE Z

8.  Mede o quão maior ou menor um valor
é em relação à média.
 z = (x – μ) / σ
 z = Escore Z (Escore padronizado)
 x = Valor desejado
 μ = Média aritmética amostral
 σ = Desvio padrão da amostra

9. Exemplos
O que significa um z-score negativo?
• O valor original é menor que 0
• O valor original é menor que a média
• O valor original é negativo
Se padronizarmos todos os valores de uma distribuição
para o escore-z, qual será o novo valor da média?
E o novo valor do desvio padrão?

10. Exemplos
Para μ = 60 e σ = 16, calcule:
• 1 σ acima da média
• 1 σ abaixo da média
• 2σ – μ
Você fez uma prova e sua nota foi 9,0. O professor
informou que a média das notas foi 6,0 e as notas
estavam distribuídas de forma normal, e que o
desvio padrão é 1,5. Onde na distribuição está sua
nota?

11. PROBABILIDADE Z
Relacionada ao score Z.
É a probabilidade de uma variável aleatória Z, ser
menor que um valor z, ou seja, o percentual de
valores z que são menores que um dado valor.

13. EXEMPLOS
Encontrar:
• p(Z < 1.65)
• p(Z > 1.65)
• p(Z < 0.01)
• p(Z < 0.01)
• p(Z < 0.00)
• p(Z < 1.96)
• p(Z < -1.96)
• p(Z > -1.96)

15. Exercício (EST008)
(Com base no gráfico)
1. Média
2. Desvio Padrão
3. Média + 2σ
4. Média - 1σ
5. Média + 1.75σ
6. Média – 2.5σ
7. Onde está 100 (Z-Score)
8. Onde está 200 (S-Score)
9. Valor de z = -0.5
10. Valor de z = 1.5

16. Qual o percentual
(aprox) de pessoas com:
1. QI menor que 85?
2. QI maior que 130?
3. QI entre 85 e 145?
4. QI menor que 145?
Exercício (EST009)
(Com base no gráfico)

17. Transforme os Valores
para o Escore Z e
Calcule:
1. P < 2.27
2. P > 0.55
3. -0.25 < P < 2.25
Exercício (EST010)
(Com base no gráfico)

18. Leitura Recomendada
 https://pt.wikipedia.org/wiki/Distribuição_nor
mal

19. Obrigado!
Dúvidas?

20. Referências
 SOARES, J. F.; FARIAS, A. A.; CESAR, C. C. Introdução à Estatística
Básica.
 BUSSAD, W. O.; MORETTIN, P. A. Estatística Básica.
 DEVORE, J. L. Probability and Statistics for Engineering and the
Sciences.
 CRESPO, Antônio – Estatística Fácil – 17ª ed. São Paulo; Saraiva,
2002.
 Grubbs, F. E. (February 1969). "Procedures for detecting outlying
observations in samples". Technometrics 11 (1): 1–21.
 Maddala, G. S. (1992). "Outliers". Introduction to Econometrics (2nd
ed.). New York: MacMillan. pp. 88–96 [p. 89].