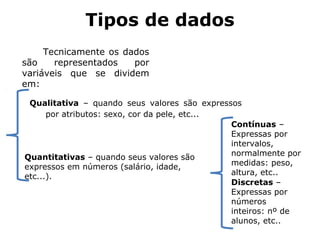
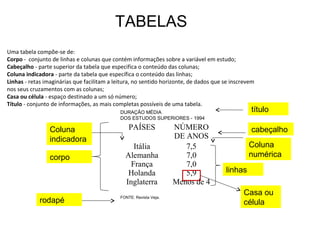
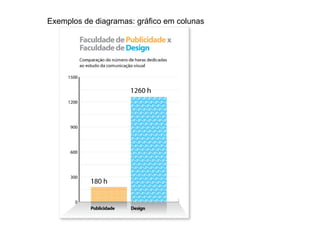
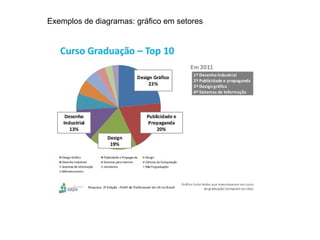
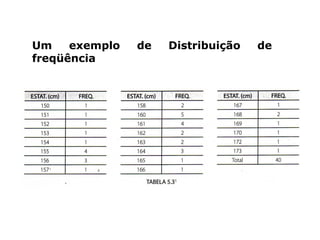
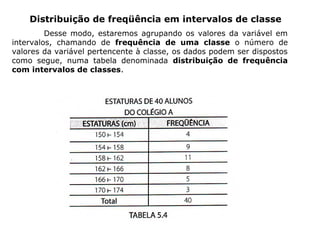
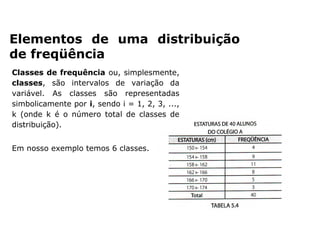
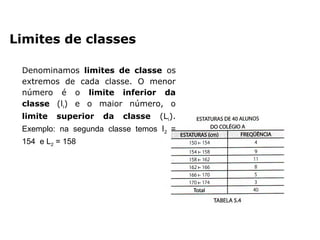
O documento fornece uma introdução sobre estatística, definindo-a como uma parte da matemática aplicada que fornece métodos para coleta, organização, análise e interpretação de dados para tomada de decisões. Apresenta os principais conceitos como população, amostra, tipos de dados, métodos estatísticos e formas de organizar e apresentar dados como tabelas e gráficos.

1. Definição de Estatística
A Estatística é uma parte da Matemática
Aplicada que fornece métodos para a
coleta, organização, descrição, análise e
interpretação de dados e para a utilização
dos mesmos na tomada de decisões.
DADOS: Consistem em
informações que vêm
de observações,
contagens, medições ou
respostas.

2. População e amostra
Ao conjunto de entes portadores de, pelo menos,
uma característica comum denominamos população
estatística ou universo estatístico.
Uma amostra é um subconjunto finito de uma população.
Ramificações
da Estatística
Descritiva: Envolve a
organização, o resumo
e a apresentação dos
dados.
Inferencial: Envolve o
uso da amostra para
chegar a conclusão
sobre uma população.

3. TIPOS DE AMOSTRAGEM
• Amostragem casual ou aleatória simples
Tipo de amostragem equivalente a um sorteio, feita ao acaso.
Ex: escolher um número qualquer da lista de presenças de uma turma.
• Amostragem proporcional estratificada
Muitas vezes a população se divide em subpopulações, estratos.
Ex: De uma a turma de 40 homes e 60 mulheres, total 100, escolher 10%: 10
pessoas ( 4 homens e 6 mulheres).
• Amostragem sistemática
A seleção dos elementos que constituirão a amostra pode ser feita por um
sistema imposto pelo pesquisador.
Ex: numa rua o pesquisador escolher apenas as casas cuja a numeração seja
ímpar.

4. Tipos de dados
Tecnicamente os dados
são representados por
variáveis que se dividem
em:
Qualitativa – quando seus valores são expressos
por atributos: sexo, cor da pele, etc...
Quantitativas – quando seus valores são
expressos em números (salário, idade,
etc...).
Contínuas –
Expressas por
intervalos,
normalmente por
medidas: peso,
altura, etc..
Discretas –
Expressas por
números
inteiros: nº de
alunos, etc..

5. Metodologia, normalmente usada na Estatística descritiva,
que visa estruturar e organizar as fases que devem ser
estabelecidas num estudo estatístico qualquer.
As principais fases do método estatístico são: Coleta de
Dados, Crítica dos Dados, Apuração dos Dados,
Apresentação dos Dados e Análise dos resultados.
FASES DO MÉTODO
ESTATISTICO

6. Uma tabela compõe-se de:
Corpo - conjunto de linhas e colunas que contém informações sobre a variável em estudo;
Cabeçalho - parte superior da tabela que especifica o conteúdo das colunas;
Coluna indicadora - parte da tabela que específica o conteúdo das linhas;
Linhas - retas imaginárias que facilitam a leitura, no sentido horizonte, de dados que se inscrevem
nos seus cruzamentos com as colunas;
Casa ou célula - espaço destinado a um só número;
Título - conjunto de informações, as mais completas possíveis de uma tabela.
PAÍSES NÚMERO
DE ANOS
Itália
Alemanha
França
Holanda
Inglaterra
7,5
7,0
7,0
5,9
Menos de 4
FONTE: Revista Veja.
DURAÇÃO MÉDIA
DOS ESTUDOS SUPERIORES - 1994
título
cabeçalho
Coluna
numérica
linhas
Coluna
indicadora
corpo
rodapé
Casa ou
célula
TABELAS

7. GRÁFICOS ESTATÍSTICOS
• Os gráficos estatísticos são representações
dos dados estatísticos, com o objetivo de
permitir uma visão mais completa e rápida
dos fatos estudados.
• Os principais gráficos são os diagramas,
gráfico polar, cartas cartográficas e
pictogramas.
• Os diagramas são os gráficos formados em
dois eixos ortogonais.

8. http://iabbrasil.net/portal/wp-
content/uploads/2013/04/img_graficos_iab
_investimento.jpg
Exemplos de diagramas: gráfico em barras

9. Exemplos de diagramas: gráfico em colunas

10. Exemplos de diagramas: gráfico em setores

11. GRÁFICO POLAR

12. CARTOGRAMA

13. PICTOGRAMA

14. ORGANIZAÇÃO DE DADOS
DADOS BRUTOS: São os dados que ainda não foram
numericamente organizados.
Exemplo: coleta da estatura de quarenta alunos, em
centímetros, que compõem uma amostra dos alunos de um
colégio A:
166, 161, 162, 165, 164, 162, 168, 156, 160, 164, 155, 163, 155, 169,
170, 154, 156, 153, 156, 158, 160, 150, 160, 167, 160, 161, 163, 173,
155, 168, 152, 160, 155, 151, 164, 161, 172, 157, 158 e 161
Rol: Certa ordenação de dados, de forma crescente ou decrescente.

15. Distribuição de
Freqüência
Quando desejamos resumir uma
grande quantidade de dados,
costumamos distribuí-los em um
arranjo tabular, denominado
distribuição de freqüência ou tabela
de freqüência.

16. Um exemplo de Distribuição de
freqüência

17. Distribuição de freqüência em intervalos de classe
Desse modo, estaremos agrupando os valores da variável em
intervalos, chamando de frequência de uma classe o número de
valores da variável pertencente à classe, os dados podem ser dispostos
como segue, numa tabela denominada distribuição de frequência
com intervalos de classes.

18. Elementos de uma distribuição
de freqüência
Classes de frequência ou, simplesmente,
classes, são intervalos de variação da
variável. As classes são representadas
simbolicamente por i, sendo i = 1, 2, 3, ...,
k (onde k é o número total de classes de
distribuição).
Em nosso exemplo temos 6 classes.

19. Limites de classes
Denominamos limites de classe os
extremos de cada classe. O menor
número é o limite inferior da
classe (li) e o maior número, o
limite superior da classe (Li).
Exemplo: na segunda classe temos l2 =
154 e L2 = 158

20. Amplitude de um intervalo
de classe, ou simplesmente
intervalo de classe, é a
medida do intervalo que define
a classe. Ela é obtida pela
diferença entre os limites
superior e inferior dessa classe
e indicada por hi.
Temos h2= L2- l2 = 158- 154 =
4 cm
iii lLh −=Amplitude de um intervalo de classe

21. Amplitude total da distribuição
Amplitude total da distribuição
(AT) é a diferença entre o limite
superior da última classe (limite
superior máximo) e o limite
inferior da primeira classe (limite
inferior mínimo).
AT = L máx – l min
Em nosso exemplo:174 – 150 = 24
cm

22. Amplitude Amostral
Amplitude Amostral(AA) é a
diferença entre o valor máximo e o
valor mínimo da amostra.
AA = x máx – x min
Em nosso exemplo:173 – 150 = 23
cm

23. Ponto médio de uma classe
Ponto médio de uma classe (xi) é, como o próprio nome
indica, o ponto que divide o intervalo de classe em duas
partes iguais. Para obtermos o ponto médio de uma classe,
calculamos a semi-soma dos limites da classe:
2
ii
i
Ll
x
+
=
Exemplo: o ponto médio da classe 2
X2 = (l2 + L2)/2 = (154 + 158)/2 =
X2 = 156 cm
X2 = 156

24. Freqüência simples ou absoluta
Frequência simples ou
frequência absoluta ou,
simplesmente, frequência de
uma classe ou de um valor
individual é o número de
observações correspondentes a
essa classe ou a esse valor. A
frequência simples é
simbolizada por fi.
Exemplos: f1 = 4, f4 = 8, etc.
A soma de todas as
freqüências é representada
por:Σ fi
Σ fi =40

25. Frequências relativas (fri) são os valores das razões entre as
frequências simples e a frequência total:
Frequência acumulada (Fi) é o total das frequências de
todos os valores inferiores ao limite superior do intervalo de
uma dada classe:
Frequência acumulada relativa (Fri) de uma classe é a
frequência acumulada da classe, dividida pela frequência total
da distribuição:
OUTROS TIPOS DE FREQUÊNCIA
i ESTATURA
( cm)
fi xi fri Fi Fri
1 150 |­­___
154 4 152 0,100 4 0,100
2 154 |­­___
158 9 156 0,225 13 0,325
3 158 |­­___
162 11 160 0,275 24 0,600
4 162 |­­___
166 8 164 0,200 32 0,800
5 166 |­­___
170 5 168 0,125 37 0,925
6 170 |­­___
174 3 172 0,075 40 1,000
∑=40 ∑=1,000

26. Distribuição de freqüência
sem intervalos de classe
Quando se trata de variável discreta de variação
relativamente pequena, cada valor pode ser tomado como um
intervalo de classe (intervalo degenerado) e, nesse caso, a
distribuição é chamada distribuição sem intervalos de
classe.