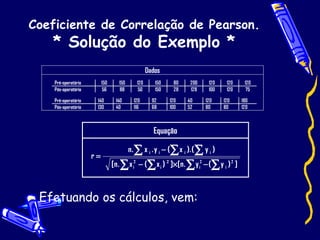
Este documento explica o coeficiente de correlação de Pearson, que é uma métrica usada para medir a força da relação linear entre duas variáveis. Ele varia de -1 a 1, onde valores mais próximos de -1 ou 1 indicam uma relação mais forte, e valores próximos de zero indicam nenhuma relação. O documento também apresenta um exemplo de cálculo do coeficiente de correlação para dados médicos e sua interpretação.

1. Inferência – Parte 4 Análise de Regressão Linear Correlação Linear.

6. Co-Variância * Definição *

14. * Solução do Exemplo * Cálculos Intermediários