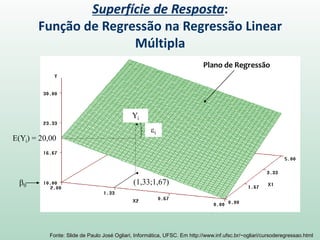
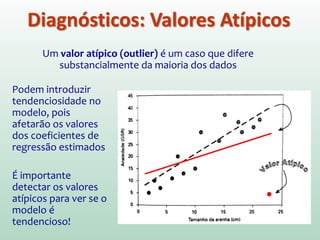
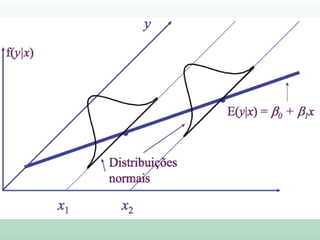
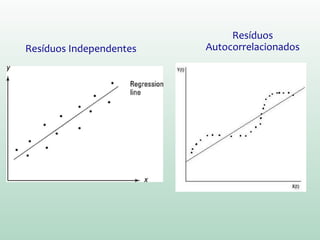
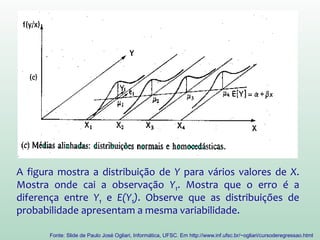
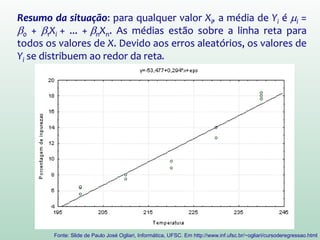
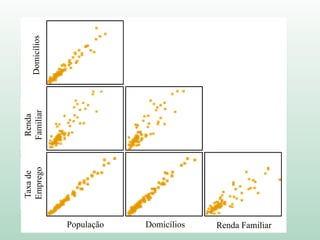
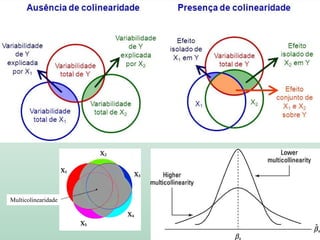
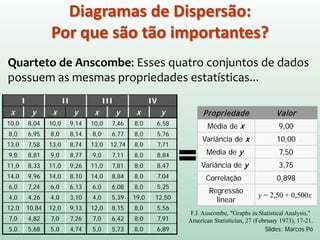
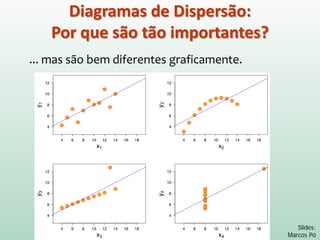
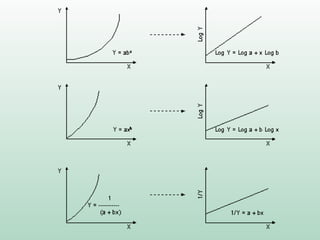
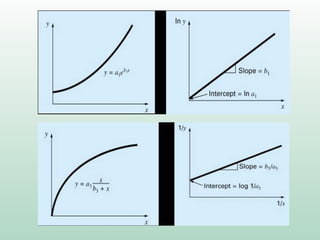
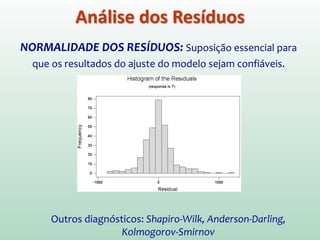
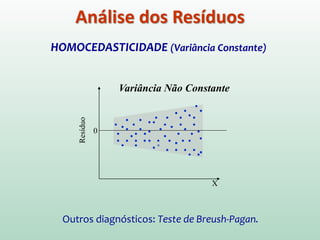
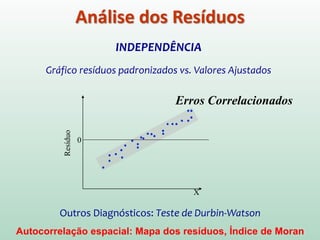
Este documento discute conceitos e métodos de análise de regressão linear. Ele explica o que é regressão simples e múltipla, como interpretar os coeficientes de regressão, e métodos para selecionar variáveis preditoras, como entrada forçada, hierárquica e passo a passo. Também aborda diagnósticos para identificar valores atípicos e casos influentes e a importância de validar se um modelo pode ser generalizado.