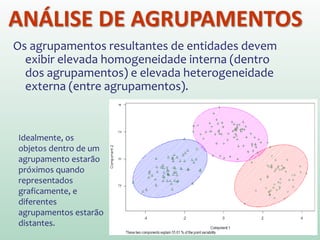
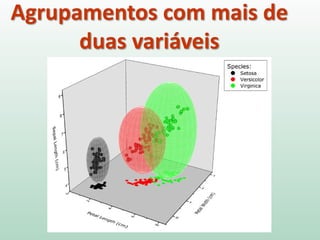
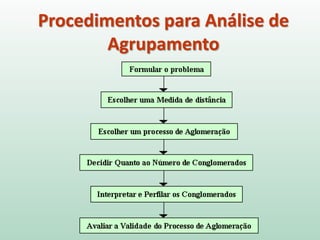
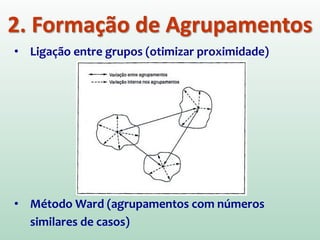
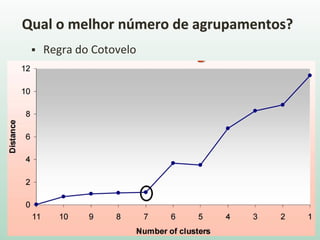
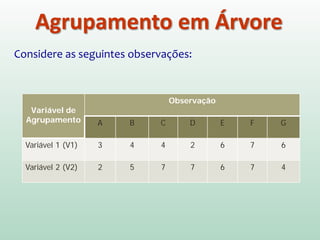
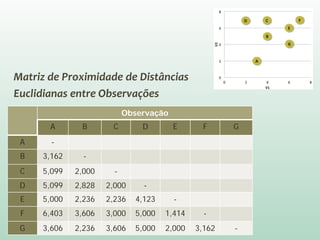
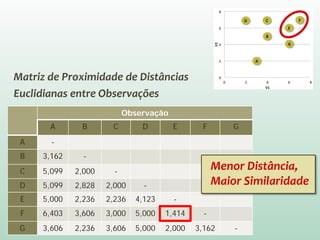
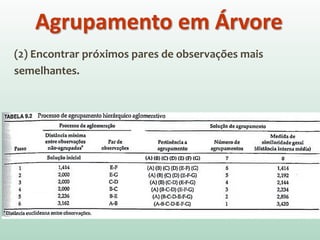
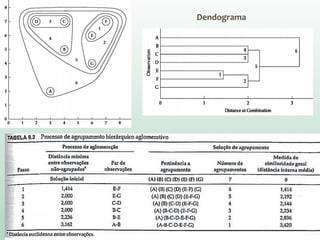
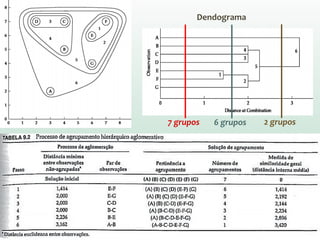
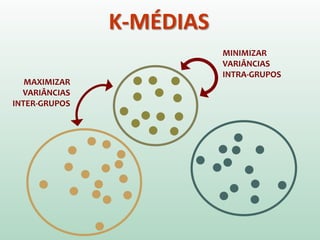
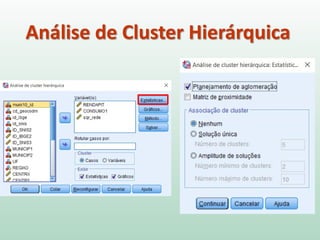
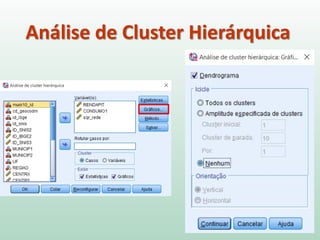
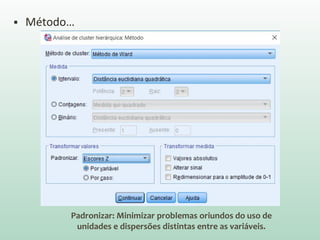
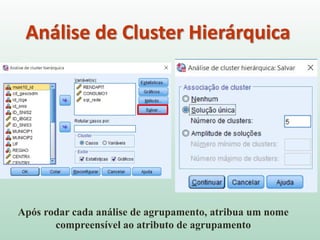
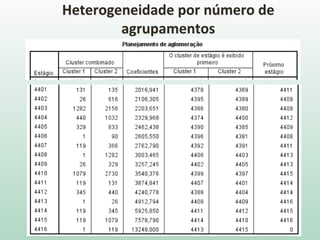
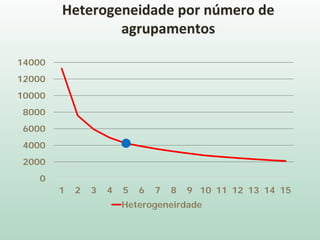
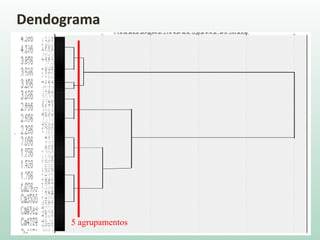
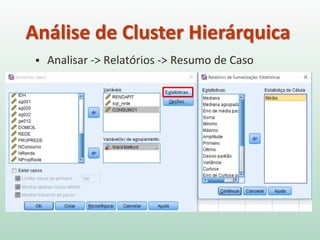
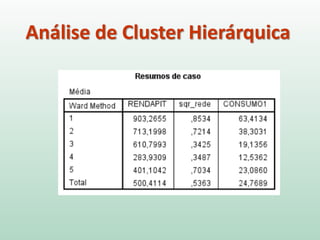
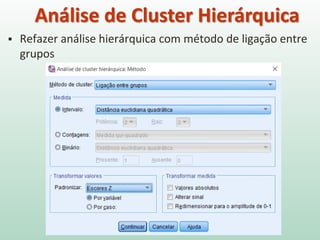
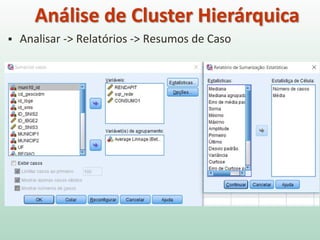
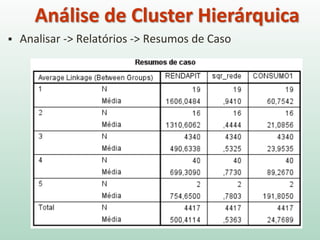
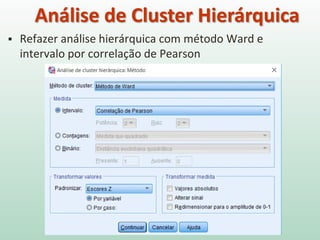
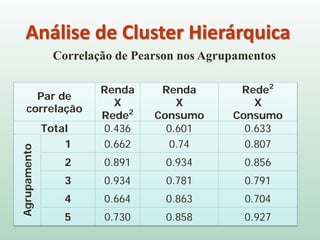
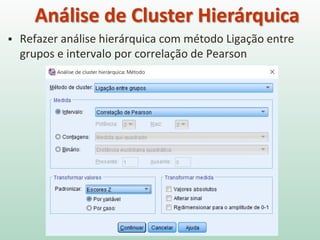
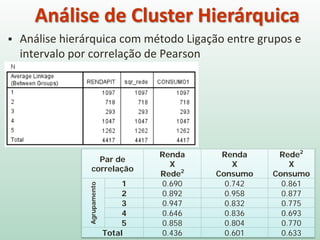
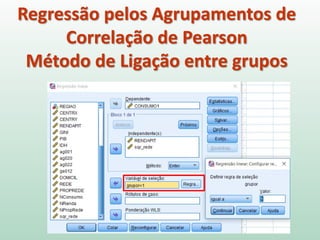
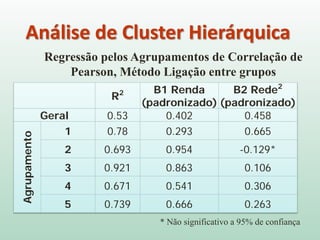
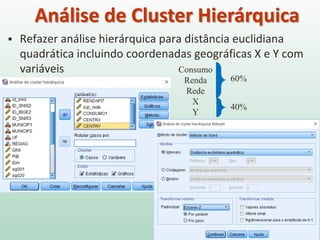
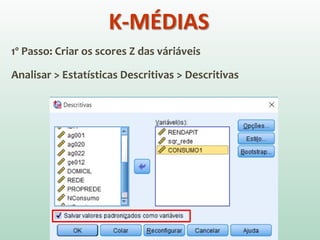
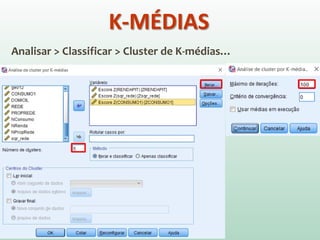
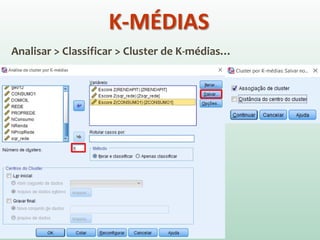
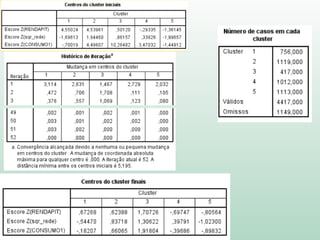
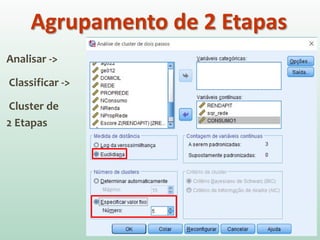
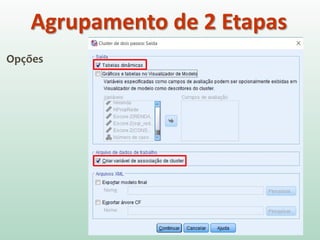
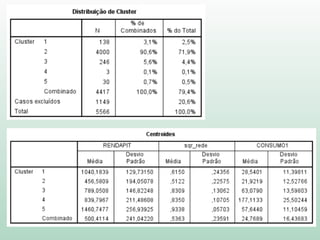
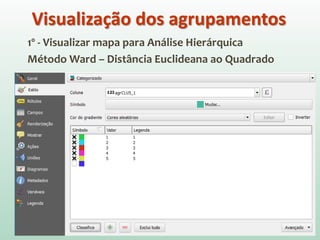
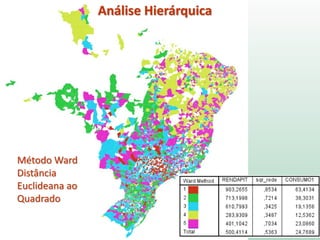
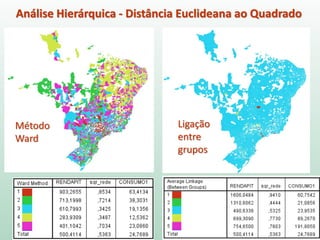
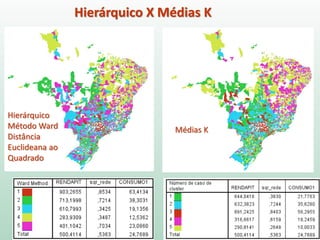
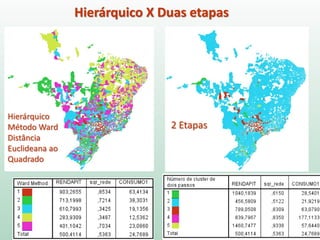
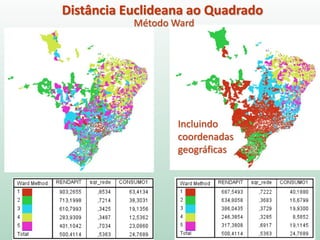
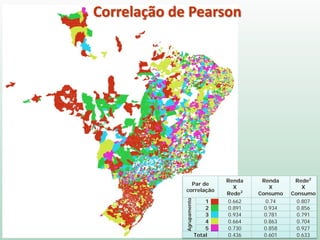
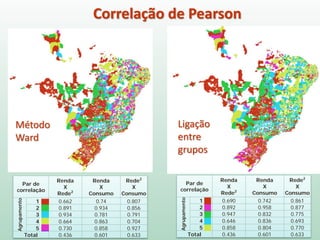
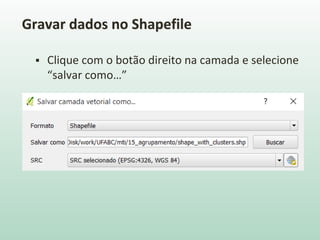
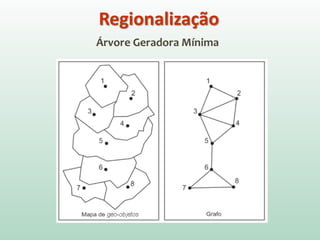
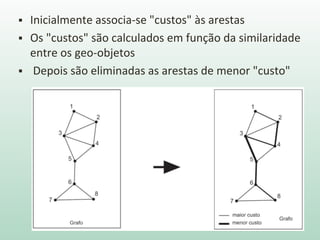
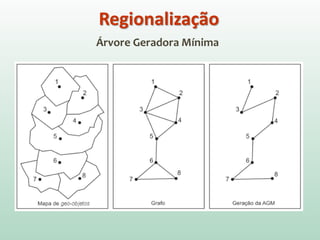
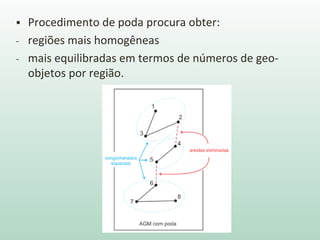
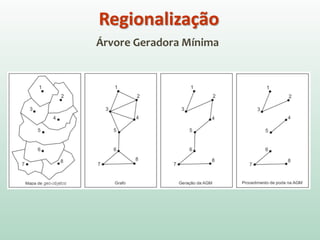
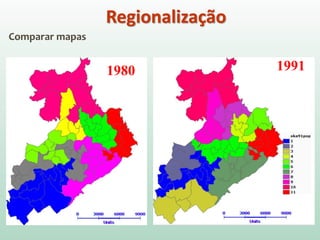
O documento discute análise de agrupamentos, um método estatístico para classificar observações em grupos homogêneos com base em suas similaridades. Aborda medidas de similaridade, métodos de agrupamento como hierárquico e k-médias, e práticas no SPSS e QGIS para visualizar os resultados espacialmente.

1. ANÁLISE DE AGRUPAMENTOS
(Cluster Analysis)
Vitor Vieira Vasconcelos
BH1350 – Métodos e Técnicas de Análise da Informação para o Planejamento
Agosto de 2016

2.  Análise de Agrupamentos
 Medidas de similaridade
 Métodos de agrupamento
 Em árvore (hierárquico)
 Médias K
 Prática no SPSS e QGIS
 Regionalização
 Método Skater
 Prática no Terraview
HAIR; BLACK; BABIN; ANDERSON; TATHAM. Análise Multivariada de Dados. 6ª ed., 2009.
Conteúdo

3. HAIR; BLACK; BABIN; ANDERSON; TATHAM. Análise
Multivariada de Dados. 6ª ed., 2009.
Capítulo 9 – Análise de Agrupamentos
Referência Principal

4. É uma técnica analítica pra identificar subgrupos
significativos de entidades homogêneas
(pessoas/objetos/lugares).
O objetivo é classificar uma amostra de entidades
em um número menor de grupos mutuamente
excludentes, com base nas similaridades entre as
entidades.
Busca por uma estrutura “natural” entre as
observações com base em um perfil multivariado.
HAIR; BLACK; BABIN; ANDERSON; TATHAM. Análise Multivariada de Dados. 6ª ed., 2009.
ANÁLISE DE AGRUPAMENTOS

5. Os agrupamentos resultantes de entidades devem
exibir elevada homogeneidade interna (dentro
dos agrupamentos) e elevada heterogeneidade
externa (entre agrupamentos).
ANÁLISE DE AGRUPAMENTOS
Idealmente, os
objetos dentro de um
agrupamento estarão
próximos quando
representados
graficamente, e
diferentes
agrupamentos estarão
distantes.

6. Agrupamentos com mais de
duas variáveis

7. 1. Classificar os setores censitários de acordo com as
diferentes dimensões de justiça/injustiça ambiental.
2. Classificar os municípios de SP em função das diferentes
dimensões de violência contra a mulher
3. Classificar os bairros do ABC de acordo com a
quantidade/perfil dos lançamentos residenciais
4. Classificar os distritos de SP de acordo com as variáveis de
infraestrutura e entorno dos domicílios
5. …
Exemplos “inspirados” nos trabalhos
propostos pelos alunos

8. Conjunto de variáveis que representam as
características usadas para comparar objetos da
análise de agrupamentos. Deve ser especificado pelo
analista.
Variável Estatística de Agrupamento

9. Procedimentos para Análise de
Agrupamento

10. Características da Análise
de Agrupamentos
1. É descritiva, não-teórica e não-inferencial
2. Sempre criará agrupamentos, independente da
existência real de alguma estrutura dos dados
3. Variedade de vias e critérios para a definição dos grupos,
o que possibilita a obtenção de soluções diferentes
4. Não é generalizável, pois é totalmente dependente das
variáveis usadas como base para a medida de
similaridade

11. QUESTÕES-CHAVE
1. Como medir similaridade?
2. Como formar os agrupamentos?
3. Quantos grupos formar?

12. 1. Medição de Similaridade
Agrupamentos são grupos de objetos semelhantes.
Precisamos, portanto, definir uma medida do grau de
similaridade/dissimilaridade entre os objetos.
É possível medir similaridade, por exemplo, de acordo com a
distância euclidiana entre cada par de observações.

13. 1. Medição de Similaridade
• Medidas de proximidade
o Distância Euclidiana (ou Euclidiana Quadrática)
o Log da Verossimilhança (logLikelihood)
Pode incluir variáveis categóricas
• Medidas de Padrões
o Coeficiente de correlação “r” de Pearson

14. 2. Formação de Agrupamentos
Definida a medida de similaridade a ser adotada,
precisamos formar agrupamentos com base na
similaridade de cada par de observações.
Esse procedimento deve determinar a pertinência a
grupo de cada observação para cada conjunto de
agrupamentos formados

15. 2. Formação de Agrupamentos
• Ligação entre grupos (otimizar proximidade)
• Método Ward (agrupamentos com números
similares de casos)

16. 3. Número de Agrupamentos
DILEMA
Menor nr. de agrupamentos &
Menor homogeneidade interna nos grupos
VS.
Maior nr. de agrupamentos &
Maior homogeneidade interna nos grupos

17. Qual o melhor número de agrupamentos?
 Regra do Cotovelo

18. Métodos de Agrupamento
1. Agrupamento em árvore (tree clustering): método
aglomerativo hierárquico
2. K-médias (k-means): método não hierárquico por
repartição
3. Duas etapas: 1º Método -> 2º Método

19. Agrupamento em Árvore
Considere as seguintes observações:
Variável de
Agrupamento
Observação
A B C D E F G
Variável 1 (V1) 3 4 4 2 6 7 6
Variável 2 (V2) 2 5 7 7 6 7 4

20. Agrupamento em Árvore
0
2
4
6
8
0 2 4 6 8
V2
V1
D C
E
F
A
B
G

21. 0
2
4
6
8
0 2 4 6 8
V2
V1
D C
E
F
A
B
G
Agrupamento em Árvore
Como medimos similaridade?
Neste exemplo, utilizaremos a
distância euclidiana (linha reta)
entre cada par de observações

22. Matriz de Proximidade de Distâncias
Euclidianas entre Observações
Observação
A B C D E F G
A -
B 3,162 -
C 5,099 2,000 -
D 5,099 2,828 2,000 -
E 5,000 2,236 2,236 4,123 -
F 6,403 3,606 3,000 5,000 1,414 -
G 3,606 2,236 3,606 5,000 2,000 3,162 -

23. Matriz de Proximidade de Distâncias
Euclidianas entre Observações
Observação
A B C D E F G
A -
B 3,162 -
C 5,099 2,000 -
D 5,099 2,828 2,000 -
E 5,000 2,236 2,236 4,123 -
F 6,403 3,606 3,000 5,000 1,414 -
G 3,606 2,236 3,606 5,000 2,000 3,162 -
Menor Distância,
Maior Similaridade

24. Agrupamento em Árvore
(1) Identificar as observações mais próximas (E e F) e
combiná-las em um agrupamento

25. Agrupamento em Árvore
(2) Encontrar próximos pares de observações mais
semelhantes.

26. Dendograma

27. Dendograma
7 grupos 6 grupos 2 grupos

28. Métodos de Agrupamento
1. Agrupamento em árvore (tree clustering): método
aglomerativo hierárquico
2. K-médias (k-means): método não hierárquico por
repartição
3. Duas etapas: 1º Método -> 2º Método

29. K-MÉDIAS
Gera k diferentes grupos com a maior distinção possível
entre eles.
Parte de k-conjuntos aleatórios e move os objetos entre
estes conjuntos com o objetivo de:
(1) Minimizar a variabilidade dentro dos conjuntos
(2) Maximizar a variabilidade entre conjuntos

30. K-MÉDIAS
MINIMIZAR
VARIÂNCIAS
INTRA-GRUPOS
MAXIMIZAR
VARIÂNCIAS
INTER-GRUPOS

33. Métodos de Agrupamento
1. Agrupamento em árvore (tree clustering): método
aglomerativo hierárquico
2. K-médias (k-means): método não hierárquico por
repartição
3. Duas etapas: 1º Método -> 2º Método

34. Agrupamentos em duas
etapas
Exemplo:
1. Análise de Agrupamento Hierárquica
2. Usa pontos centrais dos agrupamentos da análise
hierárquica para criar os primeiros conjuntos de médias K
3. Realiza as modificações aleatórias para tentar:
• Minimizar a variabilidade dentro dos conjuntos
• Maximizar a variabilidade fora dos conjuntos

35. Grupos de Entropia
• Grupos com poucos elementos, bastante diferentes
do restante da amostra
• Úteis para análise de valores atípicos

36. Prática no SPSS
• Abrir arquivo: agua&rede2010_SNIS_v2.sav
• Analisar -> Classificar -> Cluster Hierárquico

37. Análise de Cluster Hierárquica

38. Análise de Cluster Hierárquica

39.  Método…
Padronizar: Minimizar problemas oriundos do uso de
unidades e dispersões distintas entre as variáveis.

40. Análise de Cluster Hierárquica
Após rodar cada análise de agrupamento, atribua um nome
compreensível ao atributo de agrupamento

41. Heterogeneidade por número de
agrupamentos

42. Heterogeneidade por número de
agrupamentos
0
2000
4000
6000
8000
10000
12000
14000
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Heterogeneirdade

43. Dendograma
5 agrupamentos

44.  Analisar -> Relatórios -> Resumo de Caso
Análise de Cluster Hierárquica

45. Análise de Cluster Hierárquica

46.  Refazer análise hierárquica com método de ligação entre
grupos
Análise de Cluster Hierárquica

47.  Analisar -> Relatórios -> Resumos de Caso
Análise de Cluster Hierárquica

48.  Analisar -> Relatórios -> Resumos de Caso
Análise de Cluster Hierárquica

49.  Refazer análise hierárquica com método Ward e
intervalo por correlação de Pearson
Análise de Cluster Hierárquica

50. Análise de Cluster Hierárquica
Correlação de Pearson nos Agrupamentos
Par de
correlação
Renda
X
Rede2
Renda
X
Consumo
Rede2
X
Consumo
Total 0.436 0.601 0.633
Agrupamento
1 0.662 0.74 0.807
2 0.891 0.934 0.856
3 0.934 0.781 0.791
4 0.664 0.863 0.704
5 0.730 0.858 0.927

51.  Refazer análise hierárquica com método Ligação entre
grupos e intervalo por correlação de Pearson
Análise de Cluster Hierárquica

52.  Análise hierárquica com método Ligação entre grupos e
intervalo por correlação de Pearson
Análise de Cluster Hierárquica
Par de
correlação
Renda
X
Rede2
Renda
X
Consumo
Rede2
X
Consumo
Agrupamento
1 0.690 0.742 0.861
2 0.892 0.958 0.877
3 0.947 0.832 0.775
4 0.646 0.836 0.693
5 0.858 0.804 0.770
Total 0.436 0.601 0.633

53. Regressão pelos Agrupamentos de
Correlação de Pearson
Método de Ligação entre grupos

54. Análise de Cluster Hierárquica
R2 B1 Renda
(padronizado)
B2 Rede2
(padronizado)
Geral 0.53 0.402 0.458
Agrupamento
1 0.78 0.293 0.665
2 0.693 0.954 -0.129*
3 0.921 0.863 0.106
4 0.671 0.541 0.306
5 0.739 0.666 0.263
Regressão pelos Agrupamentos de Correlação de
Pearson, Método Ligação entre grupos
* Não significativo a 95% de confiança

55.  Refazer análise hierárquica para distância euclidiana
quadrática incluindo coordenadas geográficas X e Y com
variáveis
Análise de Cluster Hierárquica
Consumo
Renda
Rede
X
Y
60%
40%

56. 1º Passo: Criar os scores Z das váriáveis
Analisar > Estatísticas Descritivas > Descritivas
K-MÉDIAS

57. Analisar > Classificar > Cluster de K-médias…
K-MÉDIAS

58. Analisar > Classificar > Cluster de K-médias…
K-MÉDIAS

60. Analisar ->
Classificar ->
Cluster de
2 Etapas
Agrupamento de 2 Etapas

61. Opções
Agrupamento de 2 Etapas

63. Podemos exportar, no formato .csv ou .dbf (Dbase IV), os
resultados salvos na tabela.
Em seguida, podemos juntar esta tabela ao shapefile
(União) no QGIS e visualizar os grupos espacialmente
Visualização dos
agrupamentos

64. 1º - Visualizar mapa para Análise Hierárquica
Método Ward – Distância Euclideana ao Quadrado
Visualização dos agrupamentos

65. Análise Hierárquica
Método Ward
Distância
Euclideana ao
Quadrado

66. 2º - Visualizar mapa para Análise Hierárquica
Ligação entre grupos– Distância Euclideana ao Quadrado
Visualização dos agrupamentos

67. Análise Hierárquica - Distância Euclideana ao Quadrado
Ligação
entre
grupos
Método
Ward

68. 3º - Visualizar mapa para Médias K
Visualização dos agrupamentos

69. Hierárquico X Médias K
Distância
entre
grupos
Hierárquico
Método Ward
Distância
Euclideana ao
Quadrado
Médias K

70. 4º - Visualizar mapa para Cluster de 2 Etapas
Visualização dos agrupamentos

71. Hierárquico X Duas etapas
2 Etapas
Hierárquico
Método Ward
Distância
Euclideana ao
Quadrado

72. 5º - Visualizar mapa para análise hierárquica
Método Ward – Distância Euclideana Quadrática
Incluindo Coordenadas X e Y
Visualização dos agrupamentos

73. Distância Euclideana ao Quadrado
Incluindo
coordenadas
geográficas
Método Ward

74. 6º - Visualizar mapa para análise hierárquica
Método Ward – Correlação de Pearson
Visualização dos agrupamentos

75. Correlação de Pearson
Par de
correlação
Renda
X
Rede2
Renda
X
Consumo
Rede2
X
Consumo
Agrupamento
1 0.662 0.74 0.807
2 0.891 0.934 0.856
3 0.934 0.781 0.791
4 0.664 0.863 0.704
5 0.730 0.858 0.927
Total 0.436 0.601 0.633

76. 7º - Visualizar mapa para análise hierárquica
Método de Ligação entre Grupos – Correlação de Pearson
Visualização dos agrupamentos

77. Par de
correlação
Renda
X
Rede2
Renda
X
Consumo
Rede2
X
Consumo
Agrupamento
1 0.690 0.742 0.861
2 0.892 0.958 0.877
3 0.947 0.832 0.775
4 0.646 0.836 0.693
5 0.858 0.804 0.770
Total 0.436 0.601 0.633
Par de
correlação
Renda
X
Rede2
Renda
X
Consumo
Rede2
X
Consumo
Agrupamento
1 0.662 0.74 0.807
2 0.891 0.934 0.856
3 0.934 0.781 0.791
4 0.664 0.863 0.704
5 0.730 0.858 0.927
Total 0.436 0.601 0.633
Correlação de Pearson
Ligação
entre
grupos
Método
Ward

78. Gravar dados no Shapefile
 Clique com o botão direito na camada e selecione
“salvar como…”

79. Método Skater – Software Terraview
Referência:
Tutorial: Operações de Análise Espacial
Endereço:
http://www.dpi.inpe.br/terraview/docs/tutorial/Aula8.pdf
Regionalização

80. Método Skater
Técnica:
Minimizar a variabilidade entre os agrupamentos, mas
mantendo a contiguidade de todos os elementos em cada
agrupamento
Resultado:
Regiões relativamente homogêneas espacialmente contínuas
Regionalização

81. Árvore Geradora Mínima
Regionalização

82.  Inicialmente associa-se "custos" às arestas
 Os "custos" são calculados em função da similaridade
entre os geo-objetos
 Depois são eliminadas as arestas de menor "custo"

83. Árvore Geradora Mínima
Regionalização

84.  Procedimento de poda procura obter:
- regiões mais homogêneas
- mais equilibradas em termos de números de geo-
objetos por região.

85. Árvore Geradora Mínima
Regionalização

86. Árvore Geradora Mínima
Regionalização

87. Importar o Banco de Dados metrop_BH.mdb
Arquivo -> Banco de Dados
Regionalização

88. Selecione o tema
“Metrop_1980”
Para visualizar os
mapas, selecione um
tema e clique em
desenhar
Regionalização

89. • ICV80: Índice de Condição de Vida geral, no ano de 1980.
• DEM80: Defasagem escolar média (em anos) entre crianças de 7 a 14
anos, no ano de 1980.
• TRAB80: Porcentagem de crianças de 10 a 14 anos que trabalham, no
ano de 1980.
• AAGU80: Abastecimento adequado de água, no ano de 1980.
• TANALF80: Taxa de analfabetismo da população de 15 anos ou mais
(%), no ano de 1980.
• MANOS80: Número médio de anos de estudo (pop. de 25 anos ou
mais, no ano de 1980).
• ESP80: Esperança de vida ao nascer (em anos), no ano de 1980.
• TMI80: Taxa de mortalidade infantil (por mil nascidos vivos), no ano
de 1980.
• RENDA80: Renda familiar per capita média (Cr$1000 de 01/09/91), no
ano de 1980.
• POBRES80: Proporção de pobres (P0), no ano de 1980.
Regionalização

90. Análise -> Skater
Grupos: 10
Escolher atributos em
Plan.1 que terminem em
“80_P” (variáveis
padronizadas do ano
1980)
Regionalização

91. Regionalização

92. Regionalização

93. Para alterar a legenda
do mapa, clicar com
botão direito do mouse
sobre o tema a ser
visualizado e escolher
“Editar Legenda…”
Regionalização

94. 1- Escolher o atributo
“ska”, com precisão = 1
2- Selecione “Aplicar”
3- Selecione “Ok”
Regionalização

95. Repetir a análise para o
anos de 1991
Selecione o tema
“Metrop_1991”
Análise -> Skater
Grupos: 10
Nome da Coluna: ska91
Escolher atributos em
Plan.2 que terminem em
“91_P” (variáveis
padronizadas do ano 1991)
Regionalização

96. Comparar mapas
Regionalização
1980 1991

97. Para salvar os mapas, vá em:
Arquivo -> Salvar Tela de visualização ->Arquivo
Regionalização

98. Análise de 1980 com método de
agregação por população
Selecione o tema
“Metrop_1980”
Análise -> Skater
Grupos: 100.000 hab
Atributo: Plan1->Pop1980
Nome da Coluna: ska80pop
Escolher atributos em Plan.1
que terminem em “80_P”
(variáveis padronizadas do ano
1980)
Regionalização

99. Regionalização

100. Análise de 1980 com método de
agregação por população
Selecione o tema
“Metrop_1991”
Análise -> Skater
Grupos: 100.000 hab
Atributo: Plan2->TOTAL_91
Nome da Coluna: ska91pop
Escolher atributos em Plan.2
que terminem em “91_P”
(variáveis padronizadas do ano
1991)
Regionalização

101. Comparar mapas
Regionalização
1980 1991

102. Para salvar os mapas, vá em:
Arquivo -> Salvar Tela de visualização ->Arquivo
Regionalização

103. Exercício
Realize as seguintes análises de agrupamento para
os dados do seu trabalho de curso:
- Método Ward
- Distância Euclideana ao Quadrado
- Correlação de Pearson
- Escolha um número de agrupamentos com base
na heterogeneidade dos grupos
- Realize a regressão para cada um dos
agrupamentos de correlação de Pearson
- Exporte os resultados do SPSS para sua base de
dados do QGIS e gere os dois mapas de
agrupamento
- Interprete os resultados