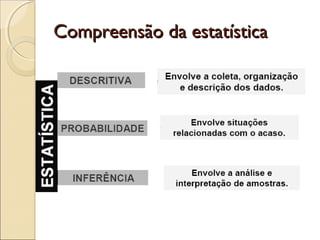
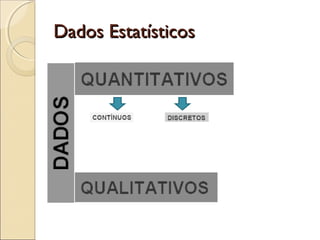
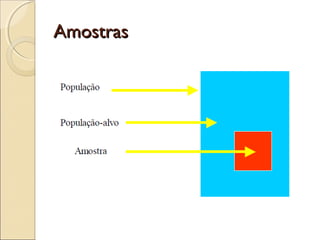
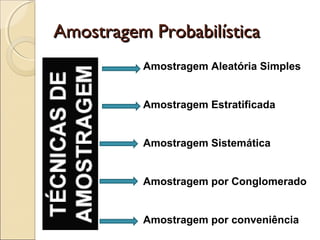
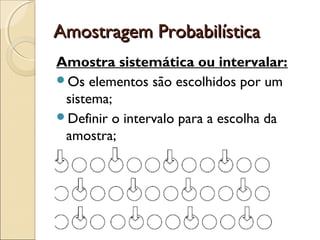
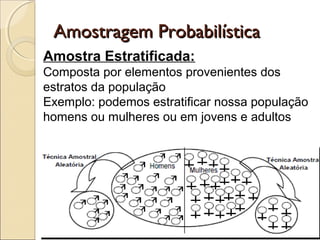
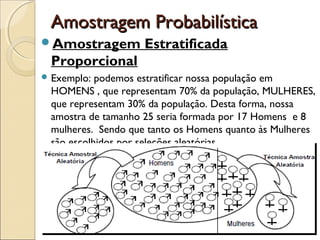
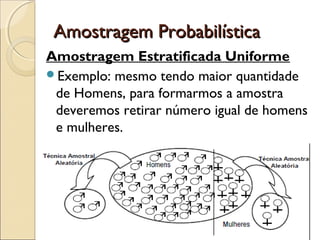
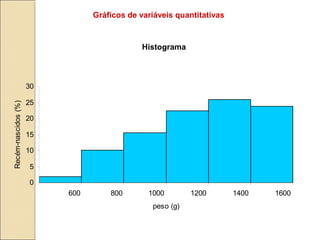
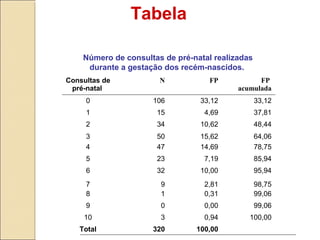
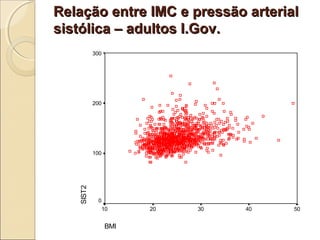
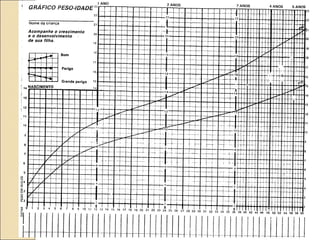
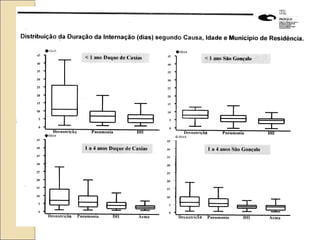
O documento discute a bioestatística, resumindo sua história desde os primeiros levantamentos estatísticos no Egito Antigo até sua expansão para áreas como saúde pública e ciências sociais. Também define bioestatística como a aplicação de métodos estatísticos para solucionar problemas biológicos e discute termos e conceitos importantes como população, amostra e parâmetros.

1. BioestatísticaBioestatística
Centro Universitário Unirondon
Curso de Graduação em Enfermagem
Ciclo III – Solidariedade Orgânica
Profª Mda. Ana Cláudia Pereira Terças
Cuiabá – MT
Março/ 2010

2. Epidemiologia e BioestatísticaEpidemiologia e Bioestatística
 O primeiro levantamento estatístico remonta a 3050
a.C., no Egito, tendo como objetivo informar o estado
sobre recursos humanos e econômicos.
 No séc. XVII d.C , dá se a expansão dos seus campos‐
de investigação a áreas como:
Saúde Pública
Indústria
Comércio
Estudos Demográficos

3. Epidemiologia e BioestatísticaEpidemiologia e Bioestatística
Fermat (1601 1665) e Pascal (1623 1662)‐ ‐
permitem que o estudo do acaso tome uma
expressão matemática, introduzindo o
Cálculo das Probabilidades.
No séc. XVIII Lambert Quetelet (1796‐
1874) introduziu a Estatística em áreas
como:
◦ Meteorologia;
◦ Antropometria;
◦ Ciências Sociais;
◦ Economia;
◦ Biologia.

4. Epidemiologia e BioestatísticaEpidemiologia e Bioestatística

5. DefiniçõesDefinições
É a aplicação dos métodos estatísticos à
solução de problemas biológicos. (Callegari-
Jacques, 2003)
Ciência que tem por objetivo orientar a
coleta, o resumo, a apresentação, a análise e
a interpretação de dados. (Barrow, 2003)
É uma coleção de métodos para planejar
experimentos, obter os dados, organizá-los,
resumi-los, analisá-los, interpretá-los e deles
extrair conclusões. (Triola, 1999)

6. Compreensão da estatísticaCompreensão da estatística

7. Termos utilizados em BioestatísticaTermos utilizados em Bioestatística
População: é a coleção completa de
todos elementos a serem estudados.
Censo: é uma coleção de dados relativos
a todos os elementos de uma população
Amostra: é uma subcoleção de
elementos extraídos de uma população.
Parâmetro/Estatística: é uma medida
numérica que descreve uma característica
da população ou amostra.

8. Dados EstatísticosDados Estatísticos

9. DadosDados
Dados Quantitativos: Consistem em
números que representam contagens ou
medidas.
Ex.: massa corporal (kg); %G; IMC; número de
repetições;.
Dados Qualitativos: Podem ser separados
em diferentes categorias que se distinguem
por alguma característica não-numérica.
Ex.: Cor de olhos; tipo de atividade;

10. Dados QuantitativosDados Quantitativos
Dados Discretos: São aquelas em que os dados
somente podem apresentar determinados
valores, em geral, números inteiros.
São limitados a valores específicos;
Raramente são expressos em fração ou decimais.
Exemplos:
- Freqüência Cardíaca;
- Número de saques.
- Número de vezes por semana que pratica
atividade física.

11. Dados QuantitativosDados Quantitativos
Dados contínuos (numéricos): São aquelas
cujos dados podem apresentar qualquer
valor dentro de um intervalo de variação
possível.
Número infinito de valores
Precisão das medidas é limitada pela
precisão do instrumento de medida.
Entre dois valores, há possibilidade infinita
de ocorrer outros valores.
Exemplo: tempo registrado (s ou min);
estatura, etc

12. AmostrasAmostras

13. Amostragem ProbabilísticaAmostragem Probabilística
Amostragem Aleatória Simples
Amostragem Estratificada
Amostragem Sistemática
Amostragem por Conglomerado
Amostragem por conveniência

14. Amostragem ProbabilísticaAmostragem Probabilística
Amostra aleatória simples:
Composta por elementos retirados ao acaso da
população (tabelas, sorteios);
Todos os elementos têm a mesma chance de
ocorrer.
33-11
22-45
21-47

15. Amostragem ProbabilísticaAmostragem Probabilística
Amostra sistemática ou intervalar:
Os elementos são escolhidos por um
sistema;
Definir o intervalo para a escolha da
amostra;

16. Amostragem ProbabilísticaAmostragem Probabilística
Amostra Estratificada:
Composta por elementos provenientes dos
estratos da população
Exemplo: podemos estratificar nossa população
homens ou mulheres ou em jovens e adultos

17. Amostragem ProbabilísticaAmostragem Probabilística
Amostragem Estratificada
Proporcional
 Exemplo: podemos estratificar nossa população em
HOMENS , que representam 70% da população, MULHERES,
que representam 30% da população. Desta forma, nossa
amostra de tamanho 25 seria formada por 17 Homens e 8
mulheres. Sendo que tanto os Homens quanto às Mulheres
são escolhidos por seleções aleatórias.

18. Amostragem ProbabilísticaAmostragem Probabilística
Amostragem Estratificada Uniforme
Exemplo: mesmo tendo maior quantidade
de Homens, para formarmos a amostra
deveremos retirar número igual de homens
e mulheres.

19. DETERMINAÇÃO DODETERMINAÇÃO DO
TAMANHO DA AMOSTRATAMANHO DA AMOSTRA
Os tamanhos das amostras são relativos, isto
é, depende do tamanho da população. Para
determinar as amostras existem várias
fórmulas, consoante o parâmetro em
critério. As mais utilizadas na saúde são as
que se baseiam na percentagem do
fenômeno .
O tamanho ótimo de uma amostra, nãoʺ ʺ
depende do tamanho da população mas sim
de dois parâmetros estatísticos: a margem de
erro e o nível de confiança

20. DETERMINAÇÃO DODETERMINAÇÃO DO
TAMANHO DA AMOSTRATAMANHO DA AMOSTRA
 Margem de erro – Uma amostra representa
aproximadamente uma população. A medida deste
aproximadamente é a chamada margem de erro: se umaʺ ʺ
pesquisa tem uma margem de erro de 2% e a Doença
Cardíaca teve 25% de prevalência na amostra, podemos dizer
que, naquele instante, na população, ela terá uma prevalência
entre 23% e 27% (25% menos 2% e 25% mais 2%).
 Nível de confiança – As pesquisas são feitas com um
parâmetro chamado nível de confiança, geralmente de 95%.
Estes 95% querem dizer o seguinte: se realizarmos uma outra
pesquisa, com uma amostra do mesmo tamanho, nas mesmas
datas e locais e com o mesmo instrumento de coleta de
dados, há uma probabilidade de 95% de que os resultados
sejam os mesmos (e uma probabilidade de 5%, é claro, de que
tudo difira).

21. Vamos Para o
Intervalo???

22. Descrição do Dados: EstatísticaDescrição do Dados: Estatística
DescritivaDescritiva
Importância da Estatística Descritiva:
Permite melhor entendimento do seu
conjunto de dados;
Permite sua forma distribuição dos
dados;
Valores centrais e medidas de dispersão
ou variação.

23. Ferramentas utilizadas pelaFerramentas utilizadas pela
Estatística DescritivaEstatística Descritiva
Histogramas;
Tabelas;
Gráfico em Setores;
Gráficos de Dispersão;
Box-plots.

24. Estatística Descritiva: HistogramasEstatística Descritiva: Histogramas
Polígonos de Freqüência ou Histogramas
 Polígonos de Freqüência: São gráficos na forma de
linhas de uma distribuição de freqüência nos quais os
valores ou os intervalos de resultados são projetados
no eixo horizontal e as freqüências associadas são
fornecidas no eixo vertical.
 Vantagens: Fácil visualização da distribuição dos
dados.
 Desvantagens: em dados contínuos e intervalares
pode resultar um um histograma confuso; não permite
visualizar os dados quando apresentados em intervalos
de dados

25. Gráficos de variáveis quantitativas
Histograma
0
5
10
15
20
25
30
600 800 1000 1200 1400 1600
peso (g)
Recém-nascidos(%)

26. Distribuição de Freqüência
É um método de tabulação ou organização
dos resultados a fim de possibilitar o
entendimento e melhor visualização do
padrão dos seus dados.
Vantagens: Pode ser realizada com dados
discretos e contínuos.
Desvantagens: podem ser confusas se não
houver categorização das variáveis contínuos
e intervalares.
Estatística Descritiva: Tabelas eEstatística Descritiva: Tabelas e
QuadrosQuadros

27. Tabela
Consultas de
pré-natal
N FP FP
acumulada
0 106 33,12 33,12
1 15 4,69 37,81
2 34 10,62 48,44
3 50 15,62 64,06
Número de consultas de pré-natal realizadas
durante a gestação dos recém-nascidos.
4 47 14,69 78,75
5 23 7,19 85,94
6 32 10,00 95,94
7 9 2,81 98,75
8 1 0,31 99,06
9 0 0,00 99,06
10 3 0,94 100,00
Total 320 100,00

28. QuadrosQuadros
DIAGNÓSTICO DE ENFERMAGEM
N %
RISCO PARA INFECÇÃO 24 100
FATORES DE RISCO N %
- Toques vaginais constantes
- Acesso Venoso Periférico
-
24
18
100
75

29. Estatística Descritiva: Gráficos emEstatística Descritiva: Gráficos em
Setores – pizzaSetores – pizza
Gráfico em Setores
São gráficos utilizados para ilustrar dados
qualitativos e nominais.
Pode-se utilizar para dados quantitativos,
uma vez que se faça a categorização da
variável.
Não se recomenda utilizar mais de 7
classes para o gráfico em setores.

30. sem anóxia
22%
moderada
37%
severa
41%
Grau de anóxia

31. Estatística Descritiva: Gráfico deEstatística Descritiva: Gráfico de
DispersãoDispersão
Gráfico de Dispersão
É um gráfico dos dados emparelhados (x,
y), com um eixo x horizontal e um eixo y
vertical.
Determinar se existe algum
relacionamento entre duas variáveis.
Quanto maior o r, maior é o
relacionamento entre as variáveis

32. Relação entre IMC e pressão arterialRelação entre IMC e pressão arterial
sistólica – adultos I.Gov.sistólica – adultos I.Gov.
BMI
5040302010
SIST2
300
200
100
0

35. Estatística Descritiva: Box PlotsEstatística Descritiva: Box Plots
Box Plots
Outro recurso pirotécnico, é o box-plot.
Vantagens: São úteis para visualizar uma
distribuição de dados.

36. Gráficos de variáveis quantitativas
Box plot
Q3 = 3° Quartil = 39
Q2 = 2° Quartil = 38
Q1 = 1° Quartil = 35
Mínimo
Q3 + 1,5 DQ = 39 + 6 = 45
DQ = 4
Observações Extremas

38. ReferênciasReferências
 - GONÇALVES, D. et al. Saberes e Praticas na
Enfermagem: A complexidade do conhecimento no
cotidiano da formação pedagógica do enfermeiro.
Florianópolis: Cidade Futura, 2005.
 - BARBETTA, Pedro Alberto. Estatística aplicada às
Ciências Sociais. 4.ed. Florianópolis:UFSC, 2001. 338p.
 - LAURENTI, Ruy et al. Estatísticas de saúde. 2 ed.rev.
São Paulo:EPU, 2006.
 - LEVIN, Jack, Estatística aplicada a Ciências
Humanas, 2ed., Tradução: Sérgio F. Costa, São Paulo:
Harbra Ltda.2000.
 - MARTINEZ, Francesc; BISQUERRA, Rafael e
SARRIERA, Jorge Castella. Introdução à estatística.
São Paulo: EPU, 2004.

39. Agora vamos praticar.... Até Amanhã!