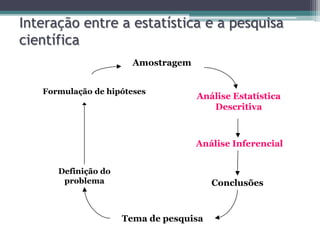
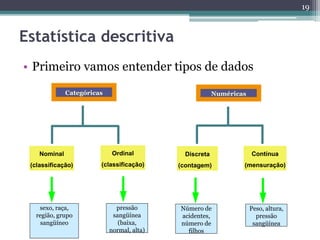
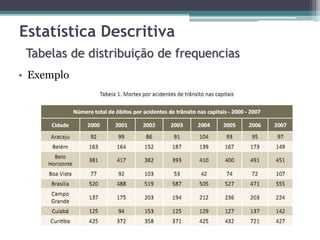
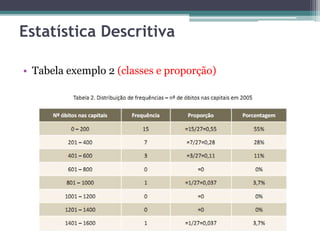
O documento apresenta um curso introdutório sobre estatística ministrado por Rodrigo Lins Rodrigues, professor da UFRPE e doutorando em ciência da computação, abordando temas como amostragem, estatística descritiva, inferência estatística e análise de regressão. Ele discute a importância da estatística na pesquisa científica e na tomada de decisões, além de mencionar softwares como o R para análise de dados. O conteúdo é estruturado de forma a fornecer tanto conceitos teóricos quanto exercícios práticos para aplicação dos conhecimentos estatísticos.